KMP 做题心得
posted on 2023-08-26 03:50:59 | under 笔记 | source
upd on 2026:远古文章,较为简单且可能有误。
前言
本文是写给自己看的,部分内容比较枯燥模糊。
\(\rm KMP\) 的作用
用于模式串匹配问题 废话。但是更多题目中关注的是其失配数组,因为失配数组 \(fail_i\) 等价于字符串 \(S\) 长度为 \(i\) 的前缀的最大 \(\rm border\)。
也就是说,借用 \(\rm KMP\) 的副产物 \(fail_i\) 可以解决很多与 \(\rm border\) 有关的问题。
-
性质 \(1\):
定义 \(p\) 为 \(S\) 的一个周期,当且仅当 \(\forall i,S_i=S_{i+p}\)。
整周期:\(p\) 整除 \(|S|\),则称 \(p\) 为 \(S\) 的一个整周期。
那么就有 \(p=|S|-border(S)\),也就是说每个 \(\rm border\) 都对应着一个周期。
其中,\(\max p=|S|-\min border(S)\),\(\min p=|S|-\max border(S)\)。
-
例题:
-
P4391 [BOI2009] Radio Transmission
求的是 \(\min p(S)\),不要求整周期。
借助性质 \(1\),直接输出 \(n-fail_n\) 即可。
测评记录。
-
P3435 [POI2006] OKR-Periods of Words
求 \(\sum \max p(S[1,i])\to \sum i-\min border(S[1,i])\)。
显然可以一直跳 \(fail\),也就是 \(j=fail_j\) 不断迭代,直到 \(fail_j=0\) 此时 \(j\) 就是 \(\min border\)。
直接写会超时。观察到 \(fail_i\) 会被遍历多次,那么考虑记忆化,直接令 \(fail_i=min border(S[1,i])\) 即可。
测评记录。
-
-
性质 \(2\):
定义 \(\rm BD(S)\) 表示 \(S\) 的所有 \(\rm border\) 集合,那么 \(\rm BD(S)=\max border(S)+BD(\max border(S))\)。
-
例题:
-
万物之根源。
题意:求两前缀的公共最长 \(\rm border\)。
观察性质 \(2\),我们发现任意 \(\rm border\) 都可被表示为 \(\dots fail_{fail_{fail_{n}}}\) 的嵌套模式,也就是说第 \(i\) 大 \(\rm border\) 可被表示为 \(fail\) 第 \(i-1\) 大 \(\rm border\)。
利用这一点,我们把不妨让 \(fail_i\to i\) 连一条边,建成的树就叫失配树(\(fail\) 树)。需要注意的是,失配树是由叶子节点指到根节点的,也就是说根为 \(0\),而 \(n\) 在最底层。
于是两前缀的公共 \(\rm border\) 实际上就是树上对应两点的公共祖先,由于从叶子走到根前缀大小不断递减,所以最大公共 \(\rm border\) 就是两点的 \(\rm LCA\)。
那么建树跑 \(\rm LCA\) 即可。不过此题没必要显性的建树,因为倍增法只关注祖先是谁,所以令 \(jump_{(i,0)}=fail_i\) 即可。
测评记录,往后遇到部分问题时就可以在放在树上思考了。
-
求所有前缀的不重叠 \(\rm border\)。
容易想到:找到最长不重叠 \(\rm border\) 然后向上跳 \(fail\) 并记录。
可以优化向上跳这一步骤,这部分的答案实际上是失配树上对应点到根这条链上的点数(没有根)。
不过还是会超时。显然成为不重叠 \(\rm border\) 的前提是它是 \(\rm border\),于是仿照求 \(fail\) 的步骤,之后直接跳 \(fail\) 找不重叠 \(\rm border\) 即可。注意 \(j\) 的值是不断传递的。
为什么传递 \(j\) 就好了?考虑 \(S[1,i-1]\) 的一个重叠 \(\rm border\) \(k\),现在要拓展一位到 \(S[1,i]\)。那么无论如何,经过上述操作后,\(k\) 的最大合法结果一定与 \(j\) 的最大合法结果相同(自己试试)。也就是说 \(j\) 可递推得到的合法结果一定包含了所有合法结果。并且这样做 \(j\) 每次至多增加 \(1\),复杂度是均摊正确的。
上面的优化就是 \(\rm KMP\) 的重要思路:传递 \(j\) 值,尽量避免重复状态。
测评记录,注意细节。
-
容易发现 \(S\) 的印章一定是 \(S\) 的 \(\rm border\),利用这一点直接暴力判断每个 \(\rm border\) 是否可以覆盖 \(S\) 即可。
(暴力可过,但也能被卡)
暴力不行,考虑 \(\rm DP\),令 \(dp_i\) 表示 \(S\) 长度为 \(i\) 的前缀的最小印章长度。
易发现,\(dp_i\) 的取值要么是 \(i\)、要么是 \(dp_{f_i}\)。对于后者,\(dp_j,j\ne BD(S[1,i])\) 的状态显然无法转移。又由性质知 \(dp_{f_i}\) 包含了 \(dp_j,j=BD(S[1,i])\) 所有情况,因此转移它不会漏解。
当然 \(S[1,i]\) 的最长 \(\rm border\) 不一定能覆盖住 \(S[1,i]\),因此再定义 \(h_{len}\) 表示长度为 \(len\) 的印章最多能完全覆盖到哪,若 \(h_{f_i}\ge i-f_i\) 则可以 \(dp_{f_i}\to dp_i\),最后用 \(i\) 更新 \(h_{dp_i}\) 即可。
(我个人感觉这种做法存在瑕疵,因为它的转移过程中只关注最小的印章,如果有最小的印章不能覆盖但次小印章可以覆盖的情况,那么上述做法是错的)
好了好了,现在讲讲真正的正解:
先将 \(S\) 的所有 \(\rm border\) 从小到大存起来,定义它们为 \(border_1...border_p\),然后逐个判断直到满足条件(暴力),需要优化。
然后发现 \(border_i\) 可以继承前面的信息。由于 \(border_i\) 是合法印章的条件是 \(S\) 中 \(border_i\) 的匹配位置的最大间距不超过 \(border_i\),那么考虑双向链表维护最大间距。
于是问题转变为链表的维护,也就是删去上一个 \(border\) 可以匹配,但当前 \(border\) 无法匹配的位置。这样会漏解吗?也就是是否会出现 \(border_{i-1},border_{i+1}\) 可以匹配,但 \(border_{i}\) 无法匹配的情况吗?显然不会,因为 \(border_{i}\) 是 \(border_{i+1}\) 的一个前缀,若后者可以匹配,则前者也可以匹配;后者无法匹配的,前者有可能可匹配,这就是维护操作的由来。
最后的问题是怎么快速找到 \(border_i\) 不可匹配,但 \(border_{i-1}\) 可匹配的位置。
继续观察,然后我们发现,若定义 \(S\) 中 \(border_i\) 的一个匹配位置(右端点)为 \(j\),则必须满足 \(border_i\) 是 \(S[1,j]\) 的一个 \(\rm border\)。这是显然的,因为 \(border_i\) 能完全覆盖 \(S[1,j]\) 的前提之一是 \(S[1,border_i-1]=S[j-border_i+1,j]\)。
联系失配树的概念,\(border_i\) 在 \(S\) 中的成功匹配位置恰好对应着失配树中 \(border_i\) 的子树中的节点。
而且失配树还有这样的性质:不同子树中的两节点 \(x,y\),其中 \(x\) 子树中的节点对应的前缀的 \(\rm border\) 不可能是 \(y\) 所对应的 \(\rm border\)(有点绕一定要仔细看看)。放在此题中就意味着 \(x\) 子树中的节点所对应的位置可以被 \(x\) 匹配,但不能被 \(y\) 匹配。
又因为 \(border_i\) 的父节点是 \(border_{i-1}\)。所以 \(border_i\) 不可匹配,但 \(border_{i-1}\) 可匹配的位置就是 \(border_{i-1}\) 的子树中除 \(border_i\) 这部分的所有节点。
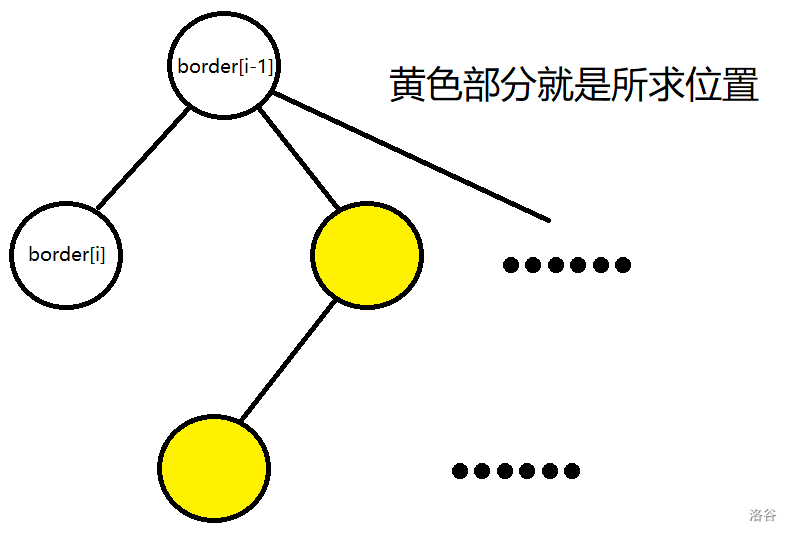
所以只需从失配树的根跑到 \(border_p\),不断删除链表中的点,并判断最大间隙是否 \(\le border_i\)。
走的是一条链,每次维护查询都是 \(O(1)\),所以复杂度为 \(O(n)\)。
写题心路:
第一眼:有点意思,不愧是 POI 的题。
写出暴力并过了后:???什么水数据。
写完 DP 后:有点意思但就这?
发现 DP 瑕疵后:什么玩意?那该咋做?
发现暴力甚至没打对还玄学过了后:数据 666。
钻研正解时:好难啊 woc。
写出来后:好耶ヽ(✿゚▽゚)ノ
-
-
杂题
-
P4824 [USACO15FEB] Censoring S
每个字符显然只会被删除、计算一次,那考虑用栈存储文本串。
那么怎么处理删掉后新出现的串呢?直接对文本串处理不好做,那么考虑让模式串的指针直接移到相应位置。
如样例中 \(momoo\) 这部分,我们删除 \(moo\) 后,直接让 \(j\) 移到之前匹配 \(mo\) 时所到的位置,也就是说接下来令 \(o\) 和 \(T_{3}=o\) 匹配即可。
具体实现的话,定义数组 \(p_i\) 记录文本串到第 \(i\) 位时,对应的模式串中所匹配到的位置。
也就是删除 \(S[i-m+1,i]\) 时,弹出栈前 \(m\) 个元素。现在栈顶元素就是文本串删除操作后的最后一个字符,让 \(j\) 移到 \(p_{st[top]}\) 即可。
看代码吧,这种思路还是很值得学习的。
-


 浙公网安备 33010602011771号
浙公网安备 33010602011771号