[trick] 删边最短路

借鉴（照搬）Alex_Wei 的图论博客。

问题介绍

• 给定无向正权图，对每条边求出删去它后 \(1\to n\) 的最短路长度。存在 \(O(m\log m)\) 做法。
• 可以拓展到非负边权的情况，复杂度不变。
• 有向正权图删边最短路是不可做问题，会了的请去申请图灵奖。
• 有向无权图删边最短路是可做问题。本文不涉及该方面内容，以后可能会补？

理论推导

先找出 \(1\to n\) 最短路径 \(P\)，分别对 \(1,n\) 建立以其为根的最短路树。记 \(T_1(x)\) 为 \(1\to x\) 的树上路径（最短路），\(T_1(x\to y)\) 为 \(x\to y\) 的树上路径。\(T_n\) 同理。我们要求 \(T_1(n)=T_n(1)=P\)。

补充几个有关最短路树的事实：

• 若 \(P(x\to y)\) 为 \(x\to y\) 的最短路，则对于任意 \(z\in P\)，\(P(x\to z)\) 也是 \(x\to z\) 的最短路。倒推即可证。
• 若已钦定 \(1\) 的一个最短路径并，则存在一种最短路树包含该路径并。这便说明了我们要求的包含 \(P\) 的最短路树一定存在。归纳每次增加一个叶子可证。

设删去的边为 \((i,j)\)，显然 \((i,j)\notin P\) 不影响最短路，所以只考虑 \((i,j)\in P\)。

记 \(A_i,A_j\) 为 \(T_1\) 删去 \((i,j)\) 后 \(i,j\) 所在子树，\(B_i,B_j\) 同理。

结论：\(A_j\cap B_i=\emptyset\)。

证明

若存在 \(u\in A_j,B_i\)，那么形如下图：

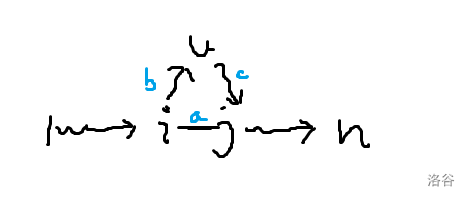
\(T_1(u)=P(1\to i)+a+c,T_n(u)=P(n\to j)+a+b\)，分别与 \(P(1\to i)+b,P(n\to j)+c\) 比较，可得 \(a+c\le b,a+b\le c\)，从而 \(2a\le 0\)，与正权边的条件矛盾。

结论：存在 \((i,j)\) 的删边最短路，形如 \(T_1(u)+(u,v)+T_n(v)\)，其中 \((u,v)\in E,(u,v)\notin T_1(i),T_n(j)\)。换句话说，只需考虑一条非树边即可。

证明

考虑调整法，对于不符合上述条件的删边最短路 \(Q\)，记 \((u,v)\in Q\) 为最后一条满足 \(u\in A_i,v\in A_j\) 的边，考虑直接将 \(Q\) 调整为 \(T_1(u)+(u,v)+T_n(v)\)，长度显然不劣于原来的，那么是否符合不经过 \((i,j)\) 呢？对于 \(T_1(u)\) 显然，因为 \(u\in A_i\)。而 \(T_n(v)\) 我们希望也有 \(v\in B_j\)，根据引理 \(A_j\cap B_i=\empty\) 可知而 \(v\in A_j\)，因此 \(v\in B_j\)。

如你所见，推导过程大量运用边的双向性，所以完全无法兼容有向图的情况。

具体实现

直接枚举 \(O(m^2)\)，不妨考虑 \((u,v)\) 能更新哪些 \((i,j)\)，满足 \((i,j)\in T_1(u)\) 的 \((i,j)\) 显然就是 \(T_1\) 中 \(lca(n,u)\) 到根路径。\(T_n\) 中同理。因此，记 \(u^\prime=lca_{T_1}(n,u),v^\prime=lca_{T_2}(1,v)\)，可以对 \(P(u^\prime \to v^\prime)\) 更新。容易 \(O(m\log m)\)。

其实也不必要求 \(P\in T_1,T_n\)，可以先建立 \(T_1\) 并找出 \(P\)，事实上 \(v^\prime\) 就是 \(v\to n\) 最短路 与 \(P\) 的第一个交点，我们可以这样构造一个满足条件的 \(T_n\)：先加入 \(P\)，然后加入 \(v\to v^\prime\) 路径，再构造其它点。正确性基于 \(v\to v^\prime + P(v^\prime \to n)\) 即为 \(v\to n\) 最短路。

\(0\) 边权的处理

推导运用了 \(w\le 0\) 制造矛盾，因此直接套用会出错。

考虑证明出错的部分，由 \(a=0\) 可得 \(b=c\)，不妨修改最小路树的定义，要求 \(T_1\) 中 \(lca(i,n)\) 的深度尽可能浅。也即强化了路径条件，要求其与 \(P\) 的交集尽可能的小。在该条件下出错情况不可能出现，因为可以调整 \(T_1\) 让 \(b\) 代替 \(c\) 接入。\(T_n\) 同理。

将 \(0\) 边缩成一个块即可，更简洁的方式是让 \(u^\prime,v^\prime\) 向上跳直到父边非零。