CSP-S T3

posted on 2024-10-26 11:36:44 | under | source

幻想：有 \(n\) 个点排成一列，若 \(A_i\) 左边第一个颜色相同的是 \(A_j=A_i\)，就将 \(i,j\) 连起来，且颜色是它们俩的颜色，0/1 分别用表示黑、白，价值是 \(A_i\)。

考察相同颜色之间的限制：同色连线不能相交或包含，但是允许端点重合。

考察不同颜色之间的限制：首先端点不能重合；其次，由题意，未被选为连线端点的点，不能同时被黑白连线跨过。

也就是说，对于相交的不同色连线，记作 \([l,r],[l2,r2],l2<r\)，则必有 \(l2=r-1\)。称为异色相交，让白色放上面、黑色放下面，则形同下图：

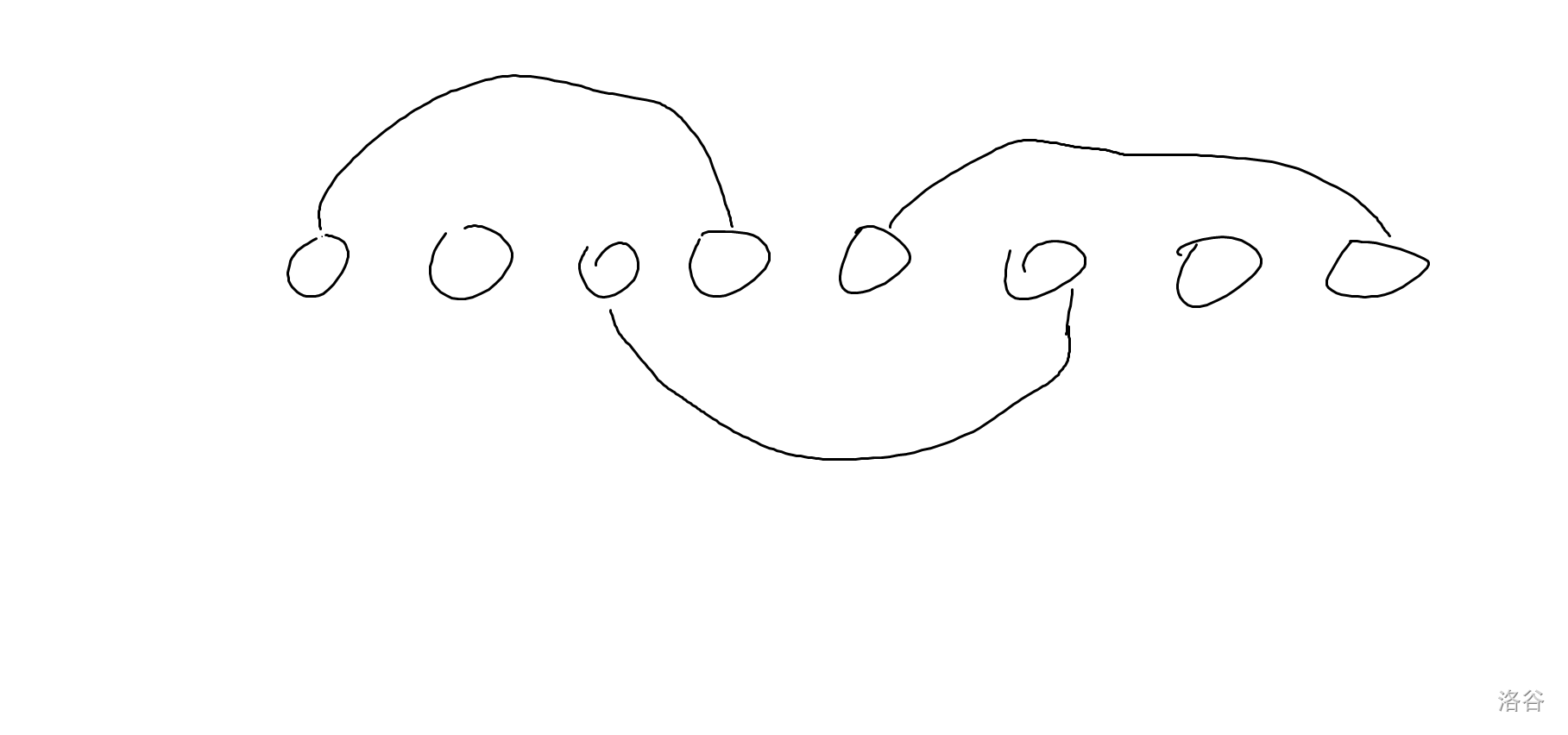
不过，当一种颜色的连线满足两端点相邻时，称为异色包含，就还可能是这样：

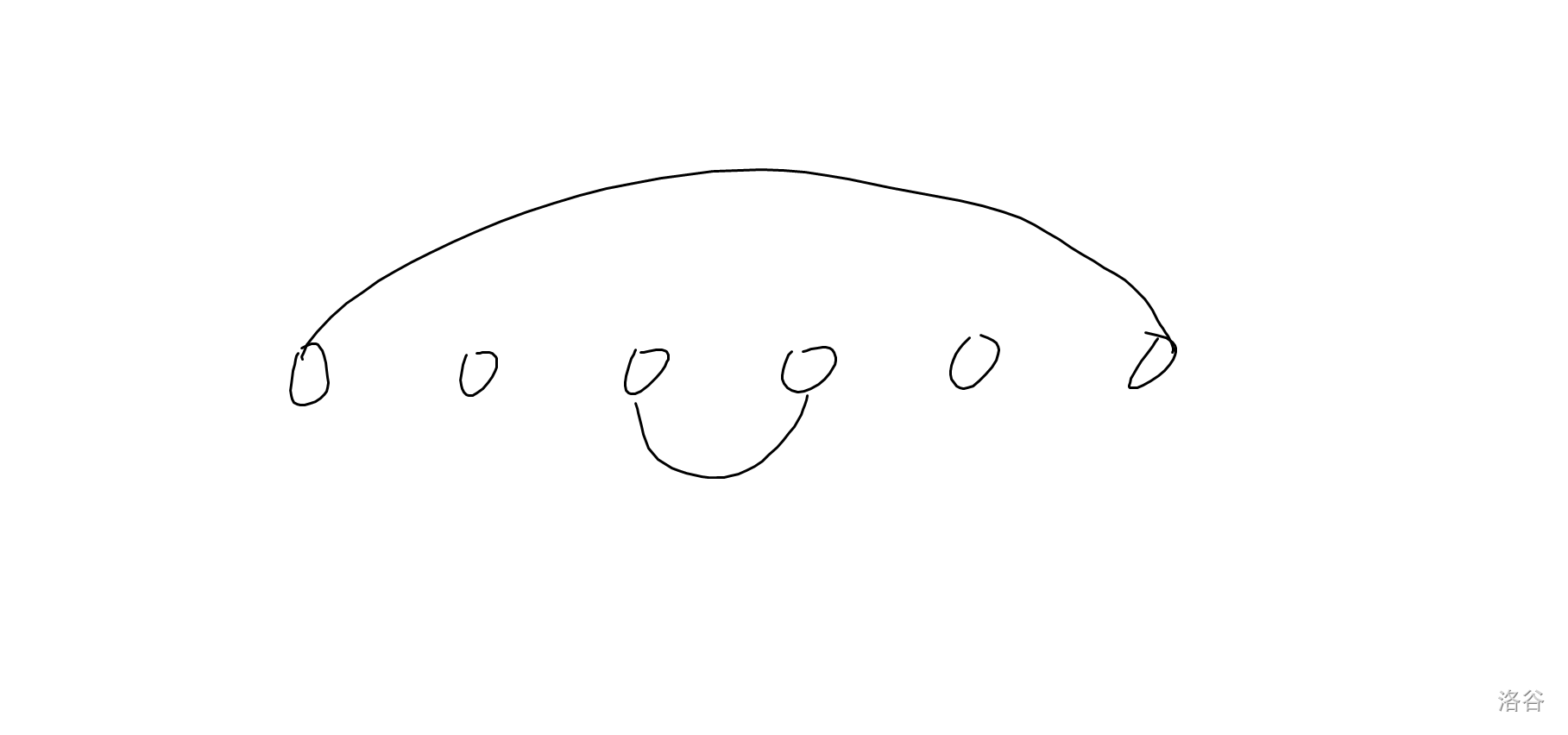
对于异色包含，不难预处理出来，记 \(s_{l,r}\) 表示考虑区间 \([l,r]\)，连线长度均为 \(2\) 时的最大价值。

考虑 dp，记 \(f_{i,0/1}\) 表示考虑前 \(i\) 个点，第 \(i\) 个点是连线右端点，\(0\) 表示强制要求点 \(i-1\) 不可和 \(i\) 同色，\(1\) 表示不做限制。再令 $g_i=\max\limits_{j\le i}{f_j,0/1} $，答案就是 \(g_n\)。

枚举左端点 \(j<i\)，转移：

• 无异色相交：\(f_{i,0/1}\gets a_i+s_{j+1,i-1}+g_j\)。
• 有异色相交：\(f_{i,0/1}\gets a_i+s_{j+1,i-1}+f_{j+1,0}\)。

那么 0/1 的区别在哪？在于 \(f_{i,0}\) 不能枚举 \(j=i-1\) 的情况。

然后 \(s_{l,r}\) 可以拆成前缀相减的形式，所以转移可以拆式子，变成只与 \(i\) 有关和只与 \(j\) 有关的两部分，对于只与 \(j\) 有关的部分，考虑拿个桶记下不同 \(a\) 对应的最大值，于是就能优化到 \(O(n)\) 啦。