7-9 dp专题1
posted on 2025-07-09 00:54:04 | under | source
By Lgx_Q??
怎么一半都做过(
P10789 [NOI2024] 登山
大记忆回复术!神仙 dp 优化题,部分分启发正解。核心在于选取 dp 转移方式(顺序)。
可能表述不严谨,意会即可。
暴力 dp
记 \(lim_i\) 为 \(d_i-h_i-1\),\(h_i\ge 0\) 所以一定是不断往上跳,且每次 \(lim\) 限制为新跳到的点。考虑跳跃过程,必然是滑到一个儿子、跳到一个祖先循环。
记 \(f_i\) 为 \(i\) 出发方案。枚举 \(j\in subtree_i\),记 \(v_{i,j}\) 为 \(i\to j\) 路径 \(lim\) 最小值,枚举 \(k\) 为跳到的祖先。若 \(d_k\in [l_j,\min(r_j,v_{i,j})]\) 则 \(f_i\gets f_k\)。
\(l_i=r_i\)
转换转移方式,枚举 \(j\),则可以转移到的 \(i\) 是祖先链一段后缀,倍增可求,\(k\) 是固定的,将转移“挂”到 \(k\) 上,算完 \(k\) 后做一次链加。
正解
因为是区间,所以做一个后缀和 \(s\),转移为 \(s_{\min(r_j,v_{i,j})}-s_{l_j-1}\)。
不妨拆贡献。对于 \(s_{l_j-1}\) 好做,和 \(l_i=r_i\) 差不多。
对于 \(s_{\min(r_j,v_{i,j})}\),这个 \(\min\) 最开始一段会取 \(r_j\),也和部分分做法差不多。此后,依次考虑每个严格后缀最小值 \(u\),\(u\) 往上一段祖先链都是被贡献 \(s_{lim_u}\)。
再次转换转移方式,枚举 \(u\),发现 \(i,j\) 独立,记 \(w_u\) 为使得 \(u\) 为后缀最小值的 \(j\) 的个数,然后仿照部分分做法只不过乘系数 \(w_u\) 就完了。
如何求 \(w_u\),建 \(lim\) 树,让 \(i\) 向第一个 \(lim\) 小于它的祖先连边。那么对于一个 \(j\) 相当于对 parent 树上其祖先链一段区间的 \(w\) 有贡献,差分即可。
P10145 [WC2024] 线段树 / P10211 [CTS2024] 线段树
用后缀和的视角看,相当于知道 \(suf_l,suf_r\) 的关系。那么将 \(l,r\) 连边,\([L,R]\) 可知当且仅当 \(L,R\) 连通。
顺走 A_zjzj 大神的图,长这样:
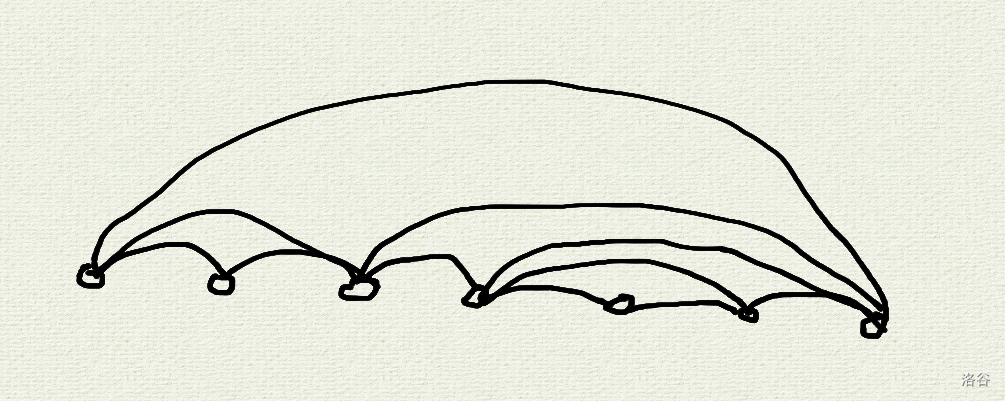
不是很优美,但你发现它的对偶图是一棵二叉树(就是原来的线段树),尝试放在对偶图上考虑:
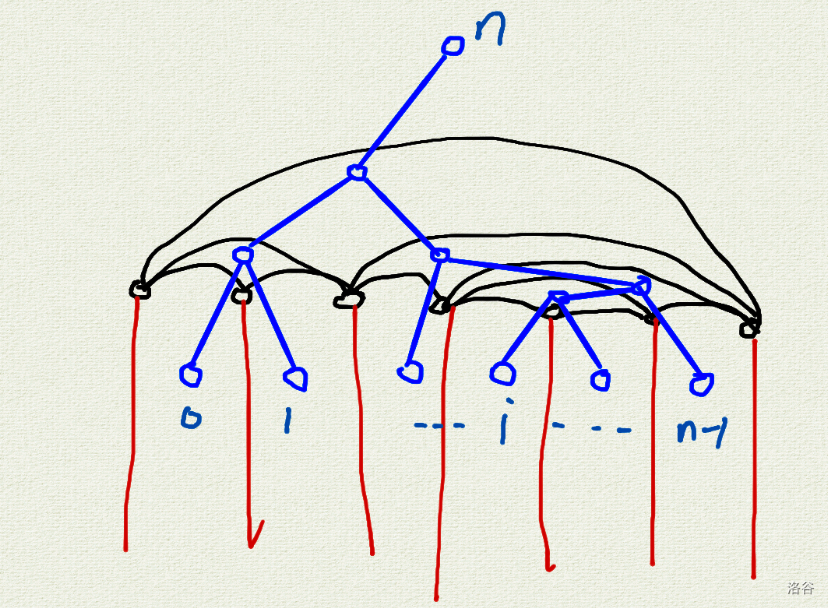
那么根据经典结论平面图路径对应对偶图割,这里将 \(l,r\) 再连边,得到面即对偶图上源点 \(s\),汇点是无限面即对偶图上 \(n\)。所以条件即为 \([l,r)\) 的叶子与其它叶子不连通。
接下来考察相交区间,例如 \(l_1\le l_2\le r_1\le r_2\),发现等价于 \([l_1,l_2),[l_2,r_1),[r_1,r_2)\)。另一种情况包含也有类似结论。因此,将区间编号视为颜色来染色,那么将得到若干等价类,条件即为不同等价类的叶子不连通。
那就可以直接 dp 了,记 \(f_{u,i}\) 为 \(u\) 子树合法且与 \(u\) 连通的颜色为 \(i\),\(g_u\) 为 \(u\) 不与任何叶子连通。转移如下:
- \(f_{u,i}=f_{ls,i}f_{rs,i}+(2g_{ls}+\sum f_{ls})(2g_{rs}+\sum f_{rs})\)
- \(g_u=(2g_{ls}+\sum f_{ls})(2g_{rs}+\sum f_{rs})\)
线段树合并即可。\(O(n\log n)\)。
QOJ9220 Bus Analysis
dp 套 dp 的一道好题口牙!揭示了 dp 套 dp 基本方法,并且需要发掘性质而不是暴搜找状态。
- 内层 dp:记 \(f_i\) 为位置 \(\le i\) 的点都被覆盖最小花费。转移枚举上个位置 \(j\) 即可。
- 内层 dp 压缩:最坏情况两点相邻,算 \(f_i\) 时需得知 \(f_{i-75}\dots f_{i-1}\) 的值,肯定会爆。但是注意到 \(f_{i-75}\dots f_{i-1}\) 的极差 \(\le 6\),因为 \(x\) 后面再放一个 \(75\) 就能转移到 \(y\)。不妨将花费均除二,那么 \(f\) 就变成了三段相同值。可以用 \((i,w,x,y,z)\) 来概括,\(w=f_i\),而 \(x,y,z\) 分别为三段结尾的 \(f\) 的下标。状态大大减少了。
- 外层 dp:直接记还是会爆,其实可以不记 \(w\),用 \(F_{i,x,y,z},G_{i,x,y,z}\) 分别记方案数和总和即可。转移分讨 \(f\) 是否 \(+1\)。\(O(n75^3)\)。
- 存在 \(O(n75^2)\) 做法,但是没必要,因为我不会。
CF506E Mr. Kitayuta's Gift
观察到转移很多是自己转移到自己,所以放到 DFA 上。
然后拆贡献分开考虑每条路径,接着将路径分为无自环与自环两部分。
最后设计出一个优秀的 DFA,借助矩阵乘法可以求出任意起终点走任意步的功能,优化跑自环部分的复杂度。
P3993 [BJOI2017] 同构(缺代码)
这题主要是发现求最大没有优美性质,转化为最小。发现是森林,然后贪心一下,就变成树的计数问题了。计数时运用了重心来处理无根树,值得借鉴。
称图 \(A\) 合法即 \(A\) 不存在非平凡自同构。
显然原图与反图的合法性相同,那么求最小值即可。
接下来证明最优解为森林:
- \(n\) 固定,等价于让边减点尽量小。而图为若干连通块,连通块必然是树的贡献最小为 \(-1\)。其它的贡献非负,不如拆为单点拼接在最大的树上。
那么森林合法,当且仅当每个树合法且互不同构。那么显然从小到大考虑点数为 \(i\) 的树最多放多少种进来,于是只需求出 \(f_n\) 为有多少种 \(n\) 阶合法树。
容易预处理出 \(h_n\) 为 \(n\) 个点无标号有根树个数,\(g_{n,m}\) 为选 \(m\) 个大小 \(\le n\) 的树的方案。然后分讨合法树的重心数量:
-
\(2\nmid n\):有且仅有一个,为 \(g_{\frac {n-1}2,n-1}\)。
-
\(2\mid n\):有一个时 \(g_{\frac n2-1,n-1}\),有两个时 \({h_{\frac n2-1}}\choose 2\)。
\(f_{262}\ge 10^{100}\) 足够了。需要高精度,好烦啊,等我有板子了再来写。
P3549 [POI2013] MUL-Multidrink
主要考察了观察性质以简化答案,最重要的是逻辑严谨地分析转移。
然后没了,代码依托。
P5979 [PA 2014] Druzyny
cdq + 线段树。
容易有暴力 dp。转移点并没有什么好的性质,但是 \(j-i\) 这一项可以拆开来分别考虑,因此试试 cdq。
好像就解决了,左右两边分别有限制:\(j\in [L_i,R_i]\)、\(i\in [L_j,R_j]\)。对于前者离线下来类似扫描线即可,对于后者在线段树上区间查询即可。\(O(n\log^2n)\)。
A_zjzj 课件里有一个复杂做法,不想研究了。
P5642 人造情感(emotion)(缺)
数据结构优化 dp。会补的。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号