7-7 贪心专题1
posted on 2025-07-07 13:01:46 | under | source
By Lgx_Q。思维含量高。
P7417 [USACO21FEB] Minimizing Edges P
题意:给一张 \(n\) 点 \(m\) 边的连通无向图,记 \(f(a,b)\) 为是否存在一条 \(1\to a\) 恰走过 \(b\) 条边的路径。构造一张图满足其 \(f\) 与原图相同,可以自环,求最小边数。\(n\le 10^5,m\le 2\times 10^5\)。
因为可以反复横跳,条件转化为每个点的奇偶最短路长度不变。
首先 \(O(n+m)\) 跑一遍奇偶最短路。假如某个点奇偶最短路都存在,则所有点都有奇偶最短路。否则,每个点最短路奇偶性唯一,保留最短路树即可,答案为 \(n-1\)。
接下来记 \(S(x,y)\) 为所有满足最短路长 \(x\)、另一个奇偶性不同的最短路长 \(y\) 的点的集合。由状态转移方程得到 \((x,y)\) 可能与哪些点相连:
- 直接连 \((x-1,y-1)\)。
- 两维分别连 \((x-1,y+1),(x+1,y-1)\)。注意另一维只能 \(+1\),也就是不能出现 \((x-1,y+3)\) 这种,这是因为无向边是双向的,会被 \((x,y)\) 更新为 \((x-1,y+1)\),不符合定义。
此外的边没有意义,所以除起点外只有上述两种情况,起点很特殊最后讨论。值得注意当 \(x+1=y\) 时 \((x+1,y-1)\) 即为 \((x,y)\)。
考虑贪心,注意到转移具有单调性,令 \(x+y\) 为行、\(y\) 为列,不妨从上到下、从右到左依次考虑。顺一张图:
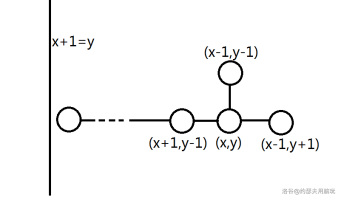
分讨:
- \(|S(x-1,y-1)|>0,|S(x-1,y+1)|=0\):只能第一种转移,连向 \((x-1,y-1)\)。
- \(|S(x-1,y-1)|=0,|S(x-1,y+1)|>0\):只能第二种转移。\((x-1,y+1)\) 可能之前钦定要连 \(t\) 条边,我们将这 \(t\) 条边用完后再考虑加边。有剩下的不管丢掉。
- \(|S(x-1,y-1)|>0,|S(x-1,y+1)|>0\):分析一下,连 \((x-1,y-1)\) 花费 \(1\),存在钦定边时连 \((x-1,y+1)\) 也花费 \(1\) 但是可以给左边贡献 \(1\) 条,否则花费 \(2\) 不划算。所以先耗尽 \((x-1,y+1)\) 钦定的边,再连 \((x-1,y-1)\)。
- \(|S(x-1,y-1)|=0,|S(x-1,y+1)|=0\):不可能,搞笑呢。
- 边界条件 \(x+1=y\):此时向左连变成了自环,一条顶两条,其它没变化。
- 起点 \(x=0\):这个非常特殊,转移只需要考虑奇数路径也就是 \(y\),所以它可以只连左边。分讨一下,若 \(y=1\) 只能连自环;反之,若右边存在点就向右边连,否则只能向上连。
用 map,\(O(n\log n)\)。
UOJ418【集训队作业2018】三角形
树上 Exchange Argument 的例题,很 Educational 啊,可以看 2022 年张隽恺的国集论文。
题意:给你 \(n\) 点有根树,\(1\) 为根。你每次可以进行两种操作:选择一个没有石子的点,若满足其儿子都有石子,将 \(w_i\) 个石子放上去;选择一个有石子的点,把石子收回来。\(n\le 2\times 10^5\)。
易知:
- 一个点只会被操作一次,操作次序为内向拓扑序。
- 一个点有石子后,立即收回其儿子的石子。
用排列刻画这个过程,记 \(p\) 为一个内向拓扑序,\(s_i=\sum\limits_{j\in son_i} w_j\)。那么答案即为:\(\max\limits_{1\le i\le n}(\sum\limits_{j=1}^i w_j-\sum\limits_{j=1}^{i-1} s_j)\)。
假如能求出 \(p\),那么有个显然的性质是子树的答案为 \(p\) 的子序列,可以用线段树合并来做。
但是内向拓扑序是不方便的,我们想要外向的。将 \(p\) 翻转得到 \(q\),注意到原式等于:\(\sum\limits_{i=1}^n (w_i-s_i) +\max\limits_{1\le i\le n}(\sum\limits_{j=1}^i s_j-\sum\limits_{j=1}^{i-1} w_j)\)。前面那一坨是根的 \(w\)。
将 \(sum,max\) 视为二元组 \((a,b)\)。初始时为 \((s_i-w_i,s_i)\),定义合并操作得到 \((a_1+a_2,\max(b_1,a_1+b_2))\)。那么答案即为依次合并二元组后的 \(b\)。
最后,设计一个满足全序的比较函数即可。从正确性出发,\((a_1,b_1),(a_2,b_2)\) 不交换答案不劣,当且仅当 \(\max(b_1,a_1+b_2)\le \max(b_2,a_2+b_1)\)。这个不满足交换律,还需调整。
用正负性分讨:
- \(a_1\le 0,a_2\le 0\):\(b_1\le b_2\)。
- \(a_1>0,a_2>0\):\(a_1+b_2\le a_2+b_1\) 即 \(a_1-b_1\le a_2-b_2\)。
- \([a_1\le 0]\ne [a_2\le 0]\):\(a_1\le a_2\)。
相当于 \(\le 0\) 的内部排序、\(\ge 0\) 的内部排序,此时分别满足全序。然后拼接起来,仍然满足全序。这样就做完了,\(O(n\log n)\)。
P3826 [NOI2017] 蔬菜
相对最容易的一题。
题意:\(n\) 种蔬菜,第 \(i\) 种有 \(c_i\) 个,单价 \(a_i\),第一个价格加上 \(s_i\),每天结束有 \(x_i\) 个变质。限定每天至多买 \(m\) 个,\(k\) 次询问,求第 \(p_i\) 天最大收益。\(n\le 10^5,m\le 10,p\le 10^5\)。
肯定尽早出售,也就是先将前面几天的 \(m\) 耗尽再考虑后面几天。所以去掉 \(p\) 时间限制,转化为总共最多卖 \(mp_i\) 个。
这样好做多了,无需时光倒流也无需模拟费用流。增量法每次多卖一个菜,贪心地优先考虑最贵的菜,看看在哪一天卖或者卖不了。同种菜优先卖晚过期的,将特价菜视作最晚过期的。
接下来先用变质限制得出最晚在哪一天卖,然后由晚到早依次判断能否这一天的 \(m\) 是否耗尽,用序列并查集维护即可。\(O(n\log n+\max (p_i)m)\)。
P5470 [NOI2019] 序列
非增量模拟费用流。懒得写了,看 cmd 的题解吧。
为了方便建模,将条件转化为至多 \(k-l\) 个自由配对(允许不对应)。那么可以通过增设 \(u,v\) 点来刻画条件。
主要思想就是建模后找出可能增广路形态,然后刻画其实际含义与限制。同时发现复杂增广路是不优的,所以把它剪枝掉了。最后大力模拟即可。
这里注释一下 cmd 题解中一些实际意义的对应:
- \(a\) 类点 \(x\) 走到 \(u\) 然后拐到 \(a\) 类点 \(y\):\(x\) 将 \(y\) 的自由配对点抢走。
- \(b\) 类点 \(x\) 走到 \(v\) 然后拐到 \(b\) 类点 \(y\):\(y\) 将 \(x\) 的自由配对点抢走。
- \(a\) 类点 \(x\) 直接走到另一侧 \(b\) 类点 \(y\):\(a\) 与 \(b\) 进行平凡配对。
- \(b\) 类点 \(y\) 直接走到另一侧 \(a\) 类点 \(x\):取消 \(a,b\) 的平凡配对。
CF2029I Variance Challenge
这转化是人能想到的?!太神了。
题意:给一个序列 \(a_1\dots a_n\),对每个 \(p=1\dots m\),求恰好进行 \(p\) 次区间加 \(k\)(\(k\) 固定)后,方差的最小值。\(nm\le 2\times 10^4\)。
关键性质:记函数 \(f(x)=\sum (a_i-x)^2\),则其最小值恰在平均数处取到,值为方差。算对称轴易证。
同时,\(x\) 的取值取决于操作区间总长度,只有 \(nm+1\) 种。直接枚举 \(x\),问题转化为:操作 \(p\) 次,最小化 \(\sum (a_i-x)^2\)。要是实际区间总长度对不上 \(x\) 怎么办?无所谓,总会有一次对上平均数的,其它的只会更大无影响。
很像模拟费用流板子 CF280D,就是那个 \(k\) 个不相交子段的。这里允许重合,所以要多开一维。
具体来说,开 \(q_{i,0}\dots q_{i,m}\),然后连 \(q_{i,0}\to q_{i,j}\) 一条容量 \(1\) 费用 \((a_i-x+jk)^2-(a_i-x+(j-1)k)^2\) 的边,再连 \(q_{i,j}\to q_{i+1,0}\) 一条边即可。但是走 \(q_{i,0}\to q_{i,j}\) 得保证 \(q_{i,1}\dots q_{i,j-1}\) 都被走过,注意到费用是关于 \(j\) 的凸函数,所以每次优先取最小就保证了不会跳着流。
甚至不用线段树直接模拟 \(O(n^2m^2)\) 能过,要开 __int128。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号