[无向图连通性] P9907 [COCI 2023_2024 #1] Mostovi

posted on 2024-06-27 05:58:22 | under | source

珂帕题。

连通性问题考虑建一棵 \(\rm dfs\) 树。注意有黑白边定理：无向图的 \(\rm dfs\) 树只存在树边、返祖边。

以 \(1\) 为根，考虑树边 \((u,v)\):

接下来以连通块（每个三角形）为单位讨论，例如有 \(A,B\) 是指存在 \(A\) 类连通块和 \(B\) 类连通块连边。

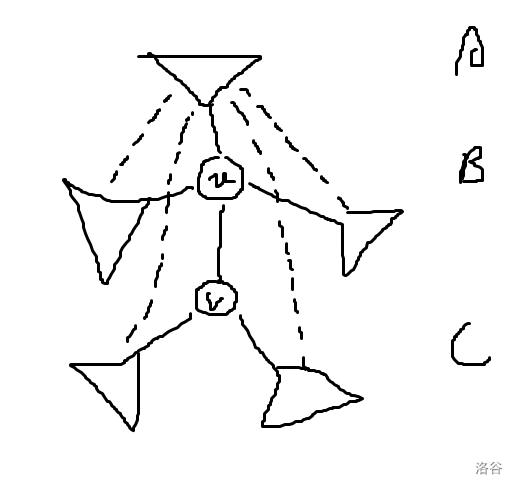
1. 此时无 \(B,C\)，所以只有同时有 $A,B\(1、\)A,C$ 时才合法。

2. 否则，必须使得 \(A,B,C\) 总计只有一个连通块。打个特判即可。

考虑非树边 \((u,v)\)，比较复杂：

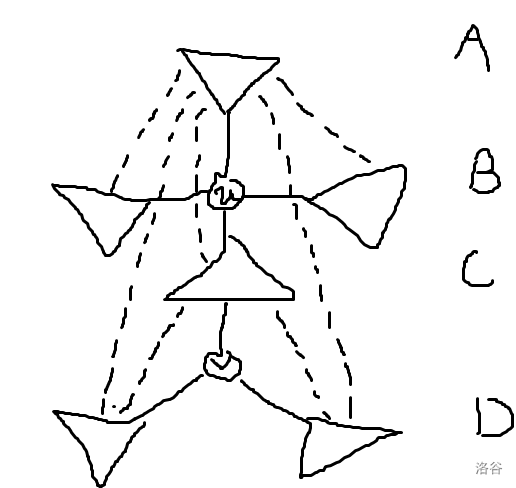
无 \(B,C\)、\(B,D\)，无 \(B,B\)、\(D,D\)。

1. 首先考虑同时存在 \(A,B\)、\(A,C\)、\(A,D\)，必然合法。

2. 否则，注意到所有 \(B\) 必须与 \(A\) 有连边，不然一定被孤立。同理，若存在 \(D\) 同时与 \(A\) 和 \(C\) 都无连边，也一定被孤立。

3. 否则，假如 \(A,C\) 有连边，一定合法。

4. 否则，可以将 \(D\) 分为：同时与 \(A,C\) 有连边、只与其一有连边。只看后者，那么原图被划分为两个大连通块，此时加上前者，就能将大连通块合二为一了。所以当且仅当存在一个 \(D\) 与 \(A,C\) 都有连边时合法。

分讨结束。怎么实现呢？注意到上文提到的 \(A,B,C,D\) 总是可以被转化为 \(dfs\) 序上 \(\le 2\) 段连续区间，然后可以线段树合并维护通过返祖边可以抵达的点。判定 \(A,B/C/D\) 维护 \(dfs\) 序最小值即可，判定 \(C,D\) 用最大值即可。