[贪心] [树形dp] P4629 [SHOI2015] 聚变反应炉

posted on 2024-04-17 15:55:38 | under | source

神秘数据分治题？

看到数据范围，很神奇吧。

先考虑前 \(10\) 个数据。由于此时 \(c_i=0/1\)，不难想到先对 \(c_i=1\) 的点操作，\(c_i=0\) 的点因为激活它没有贡献，所以最后点亮。

然后讨论激活相邻两点 \(a,b\)，满足 \(c_a=1\) 且 \(c_b=1\)。不难发现先激活 \(a\) 的花费是 \(d_a+d_b-1\)，先 \(b\) 就是 \(d_b+d_a-1\)，两者相等。又因为两种情况对外部的贡献相等，所以可以随意选择激活顺序。

推广到整棵树，这就意味着可以随意选择激活 \(c=1\) 的点的顺序。当然，这个点必须还未被激活。

然后考虑后 \(10\) 个数据。使用树形 \(\rm dp\)。

从底向上讨论下 \(u\) 的子树。可发现，其子树内部不可能出现如下情况；

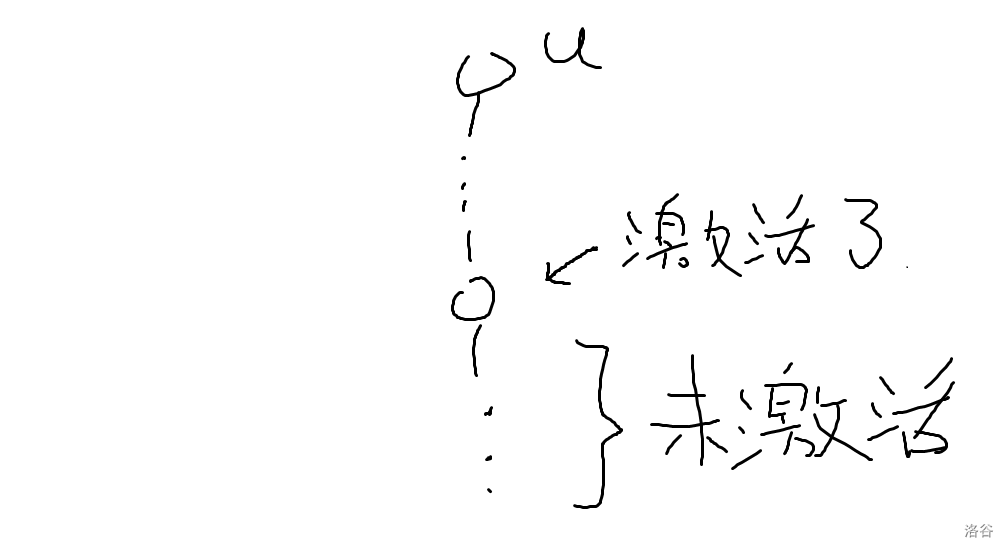
意思是：不管 \(u\) 怎么传递能量，都会在这个已激活的点上终止传递，下面没激活的就永远不会被激活了。

所以激活的点应该是从叶子开始一块块连续排列的。

但是 \(u\) 到其子树内最上面一个被激活的点的这条路径，构成一条链，肯定是不能直接枚举了。

有没有办法只枚举 \(u\) 的儿子呢？当然有，我们把这条链分为一条条边，独立转移就好了。拆分为小状态是动态规划基本思想嘛。

然后再看到 \(c\le5\)，也就是说接收到来自其它点的能量相当小，这启示我们按照它定义状态：令 \(f_{u.i}\) 表示 \(u\) 再接受 \(i\) 能量（并向下传递）即可使得整个子树都被激活时，最小花费。

转移比较显然了，将子树 \(v\) 逐个加入，枚举 \(f_{u,i},f_{v,j}\)：

若 \(i=0\)，需满足 \(c_u\ge j\)：\(f_{u,0}+f_{v,j}\to f_{u,0}\)。

若 \(j=0\)：\(f_{u,i}+f_{v,j}\to f_{u,max(0,i-c_v)}\)。

其他情况，需满足 \(c_u\ge j\)：\(f_{u,i}+f_{v,j}\to f_{u,i}\)。

（可以把转移 \(1\) 和转移 \(3\) 放在一起。）

最后是复杂度：对于 \(f_u\)，第二维的上界是 \(S_u=\sum c_{v_i}\)，\(v_i\) 是与 \(u\) 相邻节点。因为 \(\sum S_u\) 是 \(O(n)\) 级别的，所以总复杂度 \(O(n^2)\)（严格证明可参考树上背包）。

代码

#include<bits/stdc++.h>
using namespace std;

#define MIN(a, b) a = min(a, b)
const int N = 1e5 + 5, NN = 2e3 + 5;
const long long inf = 1e18;
int n, d[N], c[N], u, v;
long long f[NN][NN * 5], s[NN], lim[NN], ans, g[NN * 5];
vector<int> to[N];

inline void calc1(){
	for(int i = 1; i <= n; ++i)
		if(c[i]){
			ans += max(0, d[i]), d[i] = 0;
			for(auto v : to[i]) --d[v];
		}
	for(int i = 1; i <= n; ++i) ans += max(0, d[i]);
	cout << ans;
}
inline void dfs(int u, int fa){
	lim[u] = min(1ll * d[u], s[u]);
	for(int i = 0; i <= lim[u]; ++i) f[u][i] = d[u] - i;
	for(auto v : to[u])
		if(v ^ fa){
			dfs(v, u);
			for(int i = 0; i <= lim[u]; ++i) g[i] = f[u][i], f[u][i] = inf;
			for(int i = 0; i <= lim[u]; ++i)
				for(int j = 0; j <= lim[v]; ++j){
					if(g[i] == inf || f[v][j] == inf) continue;
					if(j == 0) MIN(f[u][max(0, i - c[v])], g[i] + f[v][j]);
					else if(c[u] >= j) MIN(f[u][i], g[i] + f[v][j]);
				}
		}
}
inline void calc2(){
	dfs(1, 0);
	cout << f[1][0];
}
int main(){
	cin >> n;
	for(int i = 1; i <= n; ++i) scanf("%d", &d[i]);
	for(int i = 1; i <= n; ++i) scanf("%d", &c[i]);
	for(int i = 1; i < n; ++i) scanf("%d%d", &u, &v), to[u].push_back(v), to[v].push_back(u), s[u] += c[v], s[v] += c[u];
	if(n > 2000) calc1();
	else calc2();
	return 0;
}