[树的直径] CF1004E Sonya and Ice Cream

posted on 2024-04-11 07:54:33 | under | source

不难猜到这条路径一定在直径上。

尝试归纳证明：如图，\(dist(A,B)\) 为直径，答案路径目前在直径上，\(D\) 是该路径的左端。现在让它往两端拓展一个点，讨论拓展后左端的最大值。

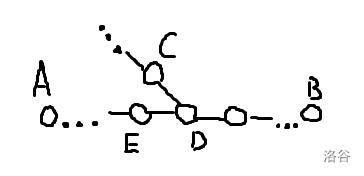
由直径性质知：假如选 \(C\)，那么最大值一定是 \(dist(A,D)\)。而选 \(E\)，则其最大值总是 \(\le dist(A,D)\)。

综上，拓展点选在直径上最优，于是这条路径会在直径上。

于是令 \(dis_u\) 表示 \(u\) 向非直径部分延伸出的最长链，\(ls_u,rs_u\) 表示 \(u\) 分别到直径两端的距离。路径 \(dist(l, r)\) 的答案就是 \(\max(\max(dis_i),ls_l,rs_r)\)。\(i\) 在该路径上。

又因为路径越长越好，因此其长度固定为 \(k\)，使用滑动窗口求 \(\max(dis_i)\) 即可。

注意暴力算 \(dis\) 不会超，因为刚好遍历整棵树，总的加起来就是 \(O(n)\)。

算法复杂度 \(O(n)\)。

代码

写的比较丑。

#include<bits/stdc++.h>
using namespace std;

#define int long long 
const int N = 1e5 + 5;
int n, k, u, v, w, tot, head[N];
int s, t, ps, D[N], lst[N], diam[N], dis[N], dc, ls[N], rs[N], ans, mx;
int q[N], l, r;
int nonono, yfz;
struct edge{int v, w, nxt;} e[N << 1];

inline void add(int u, int v, int w) {e[++tot] = {v, w, head[u]}, head[u] = tot;}
inline void dfs(int u, int fa, int d, int &p){
	if(u == nonono) return ;
	D[u] = d, lst[u] = fa; if(d > ps) ps = d, p = u;
	for(int i = head[u]; i; i = e[i].nxt) if(e[i].v ^ fa) dfs(e[i].v, u, d + e[i].w, p);
}
signed main(){
	ans = 1145141919810;
	cin >> n >> k;
	for(int i = 1; i < n; ++i)
		scanf("%lld%lld%lld", &u, &v, &w), add(u, v, w), add(v, u, w);
	ps = 0, dfs(1, 0, 0, s), ps = 0, dfs(s, 0, 0, t);
	for(int i = t; i ^ s; i = lst[i]) diam[++dc] = i; diam[++dc] = s;
	reverse(diam + 1, diam + 1 + dc);
	for(int i = 1; i <= dc; ++i) ls[i] = D[diam[i]], rs[i] = D[t] - ls[i];
	l = 1, r = 0; 
	for(int i = 1; i <= dc; ++i){
		ps = 0, nonono = diam[i + 1], dfs(diam[i], diam[i - 1], 0, yfz);
		dis[i] = ps;
		while(l <= r && i - q[l] + 1 > k) ++l;
		while(l <= r && dis[i] >= dis[q[r]]) --r;
		q[++r] = i;
		ans = min(ans, max(max(ls[max(0ll, i - k) + 1], rs[i]), dis[q[l]]));
	}
	cout << ans;
	return 0;
}