[树] P2597 [ZJOI2012] 灾难

posted on 2024-05-08 05:16:52 | under | source

这就是强省省选题吗，属实nb。

直接模拟过程肯定不行，换个角度，考虑一个点灭绝原因，让它向其它点贡献。

注意到每次只能删一个点，而点灭绝条件是其前驱均灭绝。所以需要不断找前驱直到其聚集为一个点。如下图：

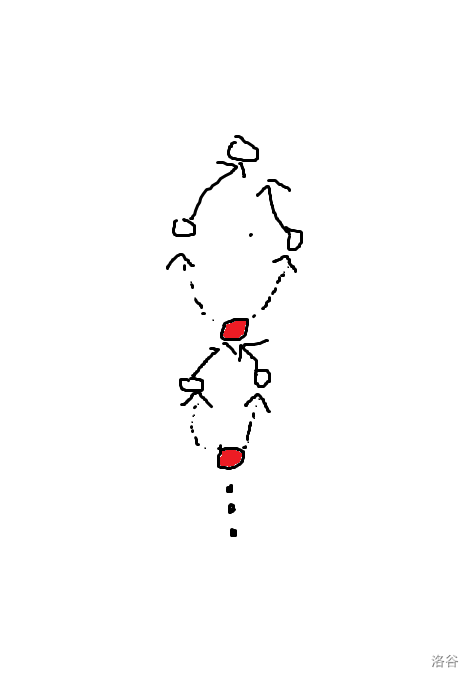
红色的点是前驱汇聚到的点，也就是可让当前点灭绝的点。

观察它们，得到以下结论：

1. 对于一个汇聚点 \(v\)，其更下面的汇聚点也是 \(v\) 的汇聚点。

2. 一个点的汇聚点一定是呈链形分布的，不会分叉。

继承性、链，联想到树。令 \(u\) 的第一个汇聚点向它连边，那么构成的树上一个点的灭绝值就是其子树大小。

那么怎么求这个汇聚点呢？其实就是其前驱在树上的 \(\rm LCA\)。

然后可以建超级源点向所有入度为 \(0\) 的点连边，避免森林。

代码

#include<bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5, M = 20;
int n, m, v, du[N], fa[N][20], dep[N], lca[N], siz[N];
queue<int> q;
vector<int> to[N], son[N];

inline int LCA(int x, int y){
	if(dep[x] < dep[y]) swap(x, y);
	for(int i = 19; ~i; --i) if(dep[fa[x][i]] >= dep[y]) x = fa[x][i];
	if(x == y) return x;
	for(int i = 19; ~i; --i) if(fa[x][i] ^ fa[y][i]) x = fa[x][i], y = fa[y][i];
	return fa[x][0];
}
inline void ins(int u, int Fa){
	fa[u][0] = Fa, dep[u] = dep[Fa] + 1;
	for(int i = 1; i < 20; ++i) fa[u][i] = fa[fa[u][i - 1]][i - 1];
}
inline void dfs(int u){
	siz[u] = 1;
	for(auto v : son[u]) dfs(v), siz[u] += siz[v];
}
signed main(){
	memset(lca, -1, sizeof lca);
	cin >> n;
	for(int i = 1; i <= n; ++i)	while(scanf("%d", &v), v != 0) to[v].push_back(i), ++du[i];
	for(int i = 1; i <= n; ++i) if(!du[i]) to[0].push_back(i), ++du[i];
	ins(0, 0), q.push(0);
	while(!q.empty()){
		int u = q.front(); q.pop();
		ins(u, lca[u]); if(u) son[lca[u]].push_back(u);
		for(auto v : to[u]){
			if(lca[v] == -1) lca[v] = u;
			else lca[v] = LCA(lca[v], u);
			if(!(--du[v])) q.push(v);
		}
	}
	dfs(0);
	for(int i = 1; i <= n; ++i) printf("%d\n", siz[i] - 1);
	return 0;
}