[决策单调性] [dp] P1973 [NOI2011] NOI 嘉年华

posted on 2024-06-06 12:14:49 | under | source

一个浅显的性质：若选择了一段区间集合（中间没有空隙），那么被这段大区间覆盖的其它区间，也一定会被选。

也就是说，问题转化为划分若干大区间，凡是被大区间覆盖的小区间都应放在一个嘉年华里。

但是，还是按小区间来分析不太方便，所以可以将所有端点离散化（类似扫描线思想），那么 \(w(i,j)\) 表示离散化后处于 \([l,r]\) 的区间个数。

那么以端点为状态设计，\(f_{i,j}\) 表示考虑前 \(i\) 个端点，嘉年华 \(A\) 选了 \(j\) 个小区间时，嘉年华 \(B\) 最多选几个小区间。

转移是容易的，于是以 \(O(n^3)\) 解决第一问。

考虑必选 \([L_i,R_i]\)，那么枚举 \(l\le L_i\le R_i\le r\)，令答案是 \(ans_{l,r}\)，问题是怎么求它？

最简单的，再预处理 \(g_{i,j}\) 表示考虑 \([i,n]\)，\(A\) 选了 \(j\) 个，\(B\) 最多选几个。

枚举 \([1,l-1],[r+1,n]\) 中某一方（因为是对称的）分别选了 \(i,j\) 个小区间，那么 \(ans_{l,r}=\max(i+j+w(l,r),f_{l-1,i}+g_{r+1,j})\)。

复杂度 \(O(n^4)\)，通过此题轻轻松松~

但是，精彩的部分在优化上，显然瓶颈在 \(ans\) 上。

令 \(\min\) 的前半部分为 \(c_1\)，后边是 \(c_2\)。观察其性质：

1. 固定 \(l,r,i\)，那么随着 \(j\) 增加，\(c_1\) 增长、\(c_2\) 减少。考虑关于 \(j\) 的函数 \(H(x)=\min(c_1,c_2)\)，呈现出前半段取 \(c_1\) 不断上升，到达某个时刻恰好 \(c_1\ge c_2\) 取到单峰，然后取 \(c_2\) 不断递减。故 \(H(x)\) 呈单峰形式。

2. 固定 \(l,r,j\)，那么随着 \(i\) 增加，\(c_1\) 增加、\(c_2\) 减少。相较于原来的 \(H\)，前半段上升、后半段下降、单峰提前出现。换句话说，一定满足 \(i+1\) 的单峰出现在 \(i\) 的单峰左边。

于是，可以用 \(j\) 从 \(H\) 的右边开始“攀爬”，更优就继续爬。

正确性：对于同一个 \(H(x)\)，是个单峰，显然是对的；若从 \(x\) 到 \(x+1\)，必然是从 \(H(x)\) 的单峰转移到 \(H(x+1)\)，不会跳到 \(H(x+1)\) 的单峰的左边。画图方便理解。

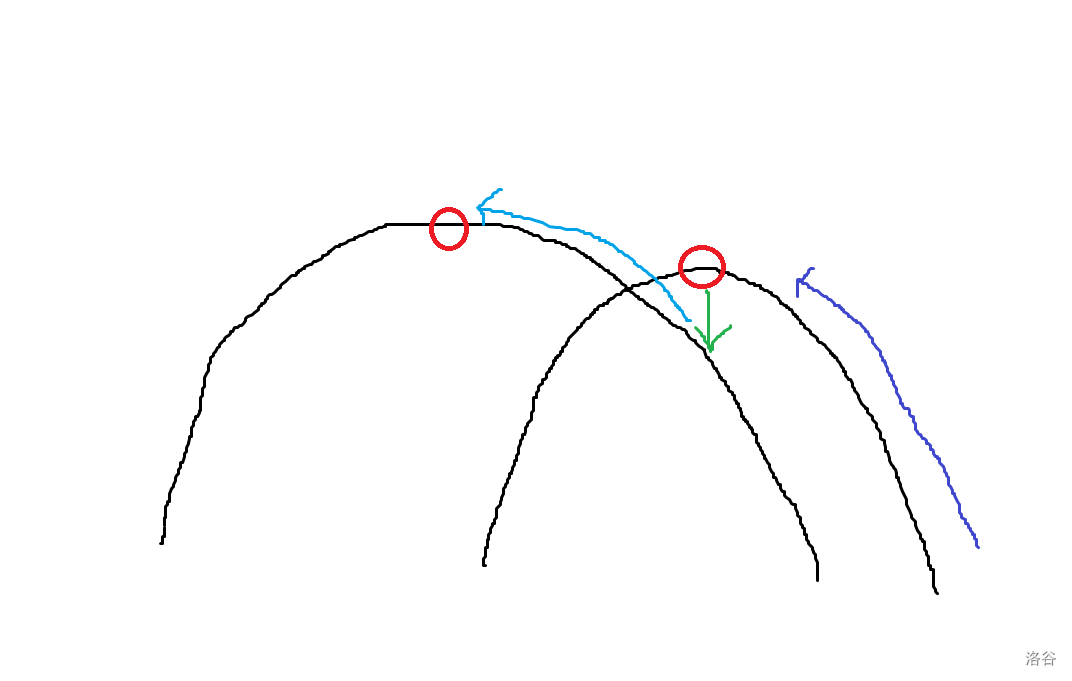
于是就优化为 \(O(n^3)\) 了。

细节：

1. 函数非严格递增、递减，所以最好用 \(\ge\) 判断是否要移动 \(y\) 指针。

2. 若两个区间重合，则会忽略只取其一的方案，\(f\) 算错，对应到 \(H(x)\) 中就是单峰突然下陷，这是致命的。怎么解决？新增转移 \(f_{i,j}=f_{i,j+1}\) 即可。

代码

#include<bits/stdc++.h>
using namespace std;

#define int long long
const int N = 2e2 + 5;
int n, b[N << 1], _n, w[N << 1][N << 1];
int f[N << 1][N], ans[N << 1][N << 1], ans1, ans2;
int g[N << 1][N], g2[N << 1][N];
struct node{int l, r;} a[N];

inline bool cmp(node A, node B) {return A.l == B.l ? A.r < B.r : A.l < B.l;}
inline int idw(int k) {return lower_bound(b + 1, b + 1 + _n, k) - b;}
inline void init(){
	sort(b + 1, b + 1 + _n);
	_n = unique(b + 1, b + 1 + _n) - b - 1;
	for(int i = 1; i <= n; ++i) a[i].l = idw(a[i].l), a[i].r = idw(a[i].r);
	for(int i = 1; i <= _n; ++i)
		for(int j = i; j <= _n; ++j)
			for(int p = 1; p <= n; ++p)
				w[i][j] += (i <= a[p].l && a[p].r <= j);
				
	memset(f, -0x3f, sizeof f), f[0][0] = 0;
	for(int i = 1; i <= _n; ++i) 
		for(int j = w[1][i]; ~j; --j){
			f[i][j] = f[i][j + 1];
			for(int p = 1; p <= i; ++p){
				if(j >= w[p][i]) f[i][j] = max(f[i][j], f[p - 1][j - w[p][i]]);
				f[i][j] = max(f[i][j], f[p - 1][j] + w[p][i]);
			}
			ans1 = max(ans1, min(j, f[i][j]));
		}
	for(int l = 1; l <= _n; ++l)
		for(int j = 0; j <= n; ++j) g[l][j] = f[l - 1][j];
		
	memset(f, -0x3f, sizeof f), f[_n + 1][0] = 0;
	for(int i = _n; i; --i) 
		for(int j = w[i][_n]; ~j; --j){
			f[i][j] = f[i][j + 1];
			for(int p = i; p <= _n; ++p){
				if(j >= w[i][p]) f[i][j] = max(f[i][j], f[p + 1][j - w[i][p]]);
				f[i][j] = max(f[i][j], f[p + 1][j] + w[i][p]);
			}
		}
	for(int r = 1; r <= _n; ++r)
		for(int j = 0; j <= n; ++j) g2[r][j] = f[r + 1][j];
		
	memset(ans, -1, sizeof ans);
}
inline void init2(){
	for(int l = 1; l <= _n; ++l)
		for(int r = l; r <= _n; ++r)
			for(int j1 = 0, j2 = n; j1 <= w[1][l - 1]; ++j1){
				while(j2 && (g2[r][j2] < 0 || min(j1 + j2 + w[l][r], g[l][j1] + g2[r][j2]) <= min(j1 + j2 - 1 + w[l][r], g[l][j1] + g2[r][j2 - 1]))) --j2;
				ans[l][r] = max(ans[l][r], min(j1 + j2 + w[l][r], g[l][j1] + g2[r][j2]));
			}
}
inline void sub2(){
	for(int i = 1; i <= n; ++i){
		ans2 = 0;
		for(int l = 1; l <= a[i].l; ++l)
			for(int r = a[i].r; r <= _n; ++r)
				ans2 = max(ans2, ans[l][r]);
		printf("%lld\n", ans2);
	}
}
signed main(){
	cin >> n;
	for(int i = 1; i <= n; ++i) scanf("%lld%lld", &a[i].l, &a[i].r), a[i].r += a[i].l - 1, b[++_n] = a[i].l, b[++_n] = a[i].r;
	init(), init2(); cout << ans1 << endl; sub2();
	return 0;
}