[广义串并联图方法] P8426 [JOI Open 2022] 放学路 _ School Road

posted on 2025-05-08 08:10:28 | under | source

题意：给一张带权无向图，判断所有 \(1\to n\) 的简单路径权值和是否相同。\(n\le 10^5,m\le 2\times 10^5\)。

考虑怎么做点双的特殊性质。因为是点双，所以可以把图看成 \(1\) 为源点、\(n\) 为汇点，然后中间夹着若干路径的图。你又看到了 \(m-n\le 13\) 的部分分，尝试用广义串并联图方法：

• 删一度点：只要不是 \(1,n\) 就删了。
• 缩二度点：显然缩成一条边没有影响。
• 叠重边：边权相等就保留一条边；反之，因为点双内必然存在经过这条边的路径，所以就输出不同。

对于最终的图，假如只有 \(1,n\) 就输出相同；反之，设权值都相同，由于该图满足 \(1\to n\) 的每条路径上的点都向外连一条边，也就是存在同胚于“杏仁图”的子图（\(1,n\) 为两端），那么简单代数推导发现横叉边权值为 \(0\)，非法。可结合下图理解：

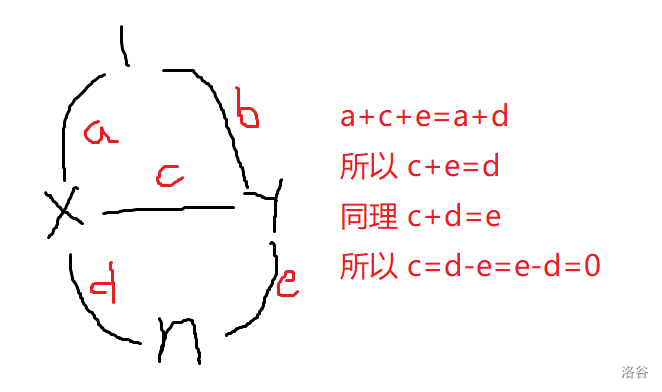
对于非点双的情况，发现对于圆方树 \(1\to n\) 路径以外的点，一走进去就不是简单路径了，所以它们都没用。剩下的点虽然不是点双，但上面用到的性质都满足了，所以套用做法即可。

\(O(m\log m)\)。

代码

#include<bits/stdc++.h>
using namespace std;

#define int long long
const int N = 2e5 + 5;
int n, m, u[N], v[N], w[N];
int dfn[N], low[N], df, vccnt, col[N], stk[N], st;
bool vis[N];
vector<int> to[N];

inline void form(int x, int u){
    int tp; bool fl = false, fl2 = false; vector<int> vc;
    do{
        tp = stk[st--];
        vc.push_back(tp);
        fl |= (tp == 1), fl2 |= (tp == n);
    }while(tp ^ x);
    vc.push_back(u);
    fl |= (u == 1), fl2 |= (u == n); 
    if(fl && fl2) for(auto i : vc) vis[i] = true; 
}
inline void dfs(int u){
    dfn[u] = low[u] = ++df, stk[++st] = u;
    for(auto v : to[u])
        if(!dfn[v]){
            dfs(v);
            low[u] = min(low[u], low[v]);
            if(low[v] >= dfn[u]) form(v, u);
        }
        else low[u] = min(low[u], dfn[v]);
}

#define id(u, v) (u * n + v)
int tot = 1, head[N], du[N], cnt;
bool used[N << 2];
struct edge{int u, v, nxt;} e[N << 2];
unordered_map<int, int> ew; 

inline void add(int u, int v) {e[++tot] = {u, v, head[u]}, head[u] = tot;}
inline int get(int u){
    while(used[head[u]]) head[u] = e[head[u]].nxt;
    return head[u];
}
inline void del(int id){
    used[id] = used[id ^ 1] = true;
    ew.erase(id(e[id].u, e[id].v)), ew.erase(id(e[id].v, e[id].u));
}
signed main(){
    cin >> n >> m;
    for(int i = 1; i <= m; ++i) scanf("%lld%lld%lld", &u[i], &v[i], &w[i]), to[u[i]].push_back(v[i]), to[v[i]].push_back(u[i]);
    to[1].push_back(n), to[n].push_back(1);
    dfs(1);
    for(int i = 1; i <= m; ++i)
        if(vis[u[i]] && vis[v[i]]){
            int bef = ew[id(u[i], v[i])];
            if(bef){
                if(w[i] ^ bef){
                    puts("1");
                    return 0;
                }
            }
            else{
                add(u[i], v[i]), add(v[i], u[i]);
                ++du[u[i]], ++du[v[i]];
                ew[id(u[i], v[i])] = ew[id(v[i], u[i])] = w[i];
            }
        }
    queue<int> q;
    for(int i = 1; i <= n; ++i){
        cnt += vis[i];
        if(i > 1 && i < n && vis[i] && du[i] == 2) q.push(i);
    }
    while(!q.empty()){
        int u = q.front(), w = 0; --cnt, q.pop();
        int ls = get(u), x = e[ls].v; w += ew[id(x, u)]; del(ls);
        int rs = get(u), y = e[rs].v; w += ew[id(u, y)]; del(rs);
        int bef = ew[id(x, y)];
        if(bef){
            if(w ^ bef){
                puts("1");
                return 0;
            }
            if(x > 1 && x < n && --du[x] == 2) q.push(x);
            if(y > 1 && y < n && --du[y] == 2) q.push(y);
            
        }    
        else{
            add(x, y), add(y, x);
            ew[id(x, y)] = ew[id(y, x)] = w;
        }    
    }
    if(cnt > 2) puts("1");
    else puts("0");
    return 0;
}