[概率] [dp] AT_abc333_f [ABC333F] Bomb Game 2

posted on 2025-04-29 10:13:03 | under | source

题意：有 \(n\) 个人，每次 \(\frac 12\) 的概率刀了最左边的人，还活着就移到最右边。重复下去直到只剩一人，对每个 \(i\) 求 \(i\) 最终存活的概率。\(n\le 3\times 10^3\)。

显然有 dp，设 \(f_{i,j}\) 为有 \(i\) 个人时第 \(j\) 个人存活的概率，转移分讨第一个人存活：

• \(f_{i,j}\gets \frac 12f_{i-1,j-1}\)。
• \(f_{i,j}\gets \frac 12f_{i,(j-1)\bmod i}\)。

把转移画出来，形如一个金字塔，答案就是最下层的点走到塔顶的乘积和（边权都是 \(\frac 12\)）：

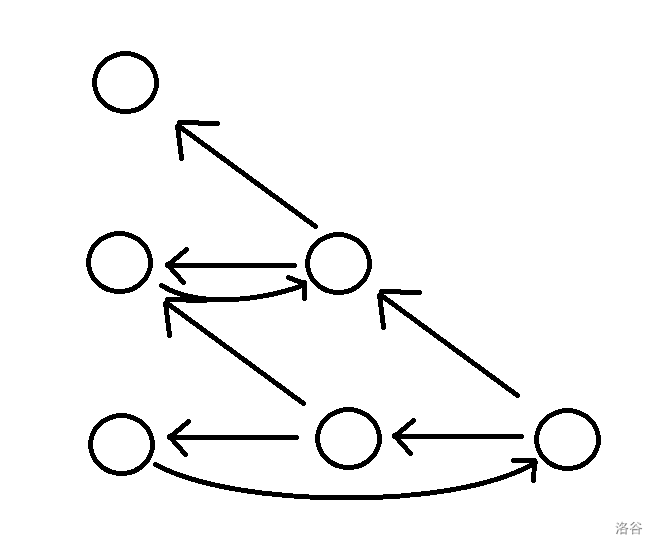
考虑路径形如：从最底层起点开始绕若干圈、在某个点停下来、走到上面一层，以此类推。所以把答案拆成两部分：不能走重复点的路径、在每一层原地转圈圈的路径。两者相乘即为答案。

对于前者，转移无环可以暴力转移做到 \(O(n^3)\)，做前后缀和状物优化一下就是 \(O(n^2)\) 了。对于后者，显然每一层可以独立算再乘起来，每一层答案用等比数列求和即可计算，\(O(n)\)。

转移比较简单，可以看代码。

代码

#include<bits/stdc++.h>
using namespace std;

#define int long long
#define ADD(a, b) a = (a + b) % mod
const int N = 3e3 + 5, mod = 998244353, inv2 = 499122177;
int n, f[N][N], pw[N], h[N];

inline int qstp(int a, int k) {int res = 1; for(; k; a = a * a % mod, k >>= 1) if(k & 1) res = res * a % mod; return res;}
signed main(){
    pw[0] = 1;
    for(int i = 1; i < N; ++i) pw[i] = pw[i - 1] * inv2 % mod;
    cin >> n;
    f[1][1] = h[1] = 1;
    for(int i = 2; i <= n; ++i){
        for(int j = 1, ps = 0; j <= i; ++j){
            ps = (ps * inv2 % mod + f[i - 1][j - 1]) % mod;
            ADD(f[i][j], inv2 * ps % mod);
        }
        for(int j = i, ns = 0; j; --j){
            ns = (ns * 2ll % mod) % mod;
            ADD(f[i][j], pw[1 + i] * ns % mod);
            ADD(ns, f[i - 1][j - 1]);
        }
        h[i] = qstp(1 - pw[i] + mod, mod - 2) % mod * h[i - 1] % mod; 
    }
    for(int i = 1; i <= n; ++i) printf("%lld ", f[n][i] * h[n] % mod);
    return 0;
}