[博弈论] [转化] [AGC002E] Candy Piles

posted on 2024-05-21 05:18:30 | under | source

无敌牛子题。

令 \(a_1\dots a_n\) 降序排序。

然后转化问题，构建出一个矩阵，第 \(i\) 行是一个高为 \(a_i\) 的矩形。

于是操作 \(1\) 对应 \((x,y)\to (x+1,y)\)，操作 \(2\) 对应 \((x,y)\to (x,y+1)\)。

容易有递推：\(s_{x,y}=[\min(s_{x,y+1},s_{x+1,y})=0]\)。

走出矩阵获胜，即轮廓为 \(1\)。因为面临的局面是空，对手已经取完输了。

然后尝试打表找个规律，发现朝右的对角线上的 \(s\) 相等，即 \(s_{x,y}=s_{x+1,y+1}\)，当然不包括轮廓。应该可证？

于是直接找到 \((1,1)\) 对应的对角线上最后一个点 \((x,y)\)，计算 \(s_{x,y}\)。

令 \(h,l\) 分别为 \((x,y)\) 向右、向上走多少步才能出去，则有 \(s_{x,y}=[\min(h\bmod 2, l\bmod 2)=1]。\)

证明

补充下重要结论 \(s_{x,y}=s_{x+1,y+1}\) 的证明。

其实就是反推 \(s\)。施反证法，如下图所示：

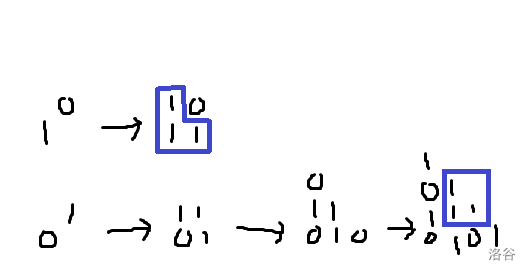
显然都矛盾了，故结论成立。

代码

#include<bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;
int n, a[N], x, y, H, L;

inline bool cmp(int a, int b) {return a > b;}
signed main(){
	cin >> n;
	for(int i = 1; i <= n; ++i) scanf("%d", &a[i]);
	sort(a + 1, a + 1 + n, cmp);
	for(int i = 1; i <= n; ++i)	if(a[i + 1] <= i || i == a[i]) {x = y = i; break;}
	H = a[x] + 1 - y;
	for(int i = x; i <= n + 1; ++i) if(y > a[i]) {L = i - x; break;}
    printf("%s", (min(H % 2, L % 2) == 0) ? "First" : "Second");
	return 0;
}