[trie] [贪心] P3294 [SCOI2016] 背单词

posted on 2024-06-13 04:39:21 | under | source

傻逼出题人，表达能力差的要死，就这题意谁看了不迷糊。

整理后的题意：

对于第 \(x\) 个学习的单词：

• 若存在单词是其后缀，但尚未被学习，花费 \(n^2\)。

• 若不存在单词是其后缀，花费 \(x\)。

• 若其所有后缀都被学习，记其中最后一个学习的标号为 \(y\)，花费 \(x-y\)。

求最小花费？

首先反转一下变成前缀，就能用 \(\rm trie\) 了。

我们将一串连续前缀看成一组，如 \(\{a,abc,abcde\}\)。

显然一组内的位置必须递增，这样最多也就 \(\frac {n(n+1)}2\)，否则会至少产生 \(n^2\) 的代价必然不优。

然后缩一下建好的 \(\rm trie\)，让所有点相邻。

于是变成了树上问题，假如已经计算好了子树 \(v_i\) 的答案，那么容易发现，不会在不同子树内反复横跳，即同一子树的位置要连续一段。容易调整法证明：

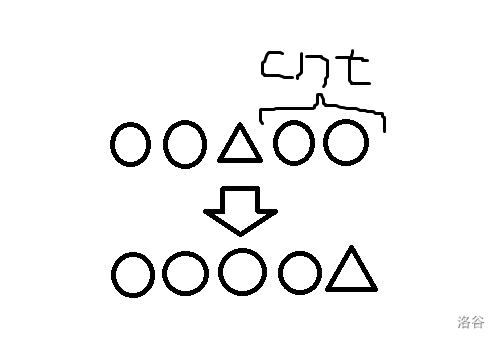
不同形状代表不同子树。调整后三角形代价 \(+cnt\)，但是后面的那串圆形代价 \(-cnt\)，所以不劣。其余情况同理。

然后从子树 \(v_1\) 后面接子树 \(v_2\) 的额外代价是 \(siz_{v_1}\)，那么容易有贪心：按照子树大小从小到大排。

注意：以上的分析都基于压缩后的 \(\rm trie\)，如果不压缩直接做会错（无端出现了 \(\rm lca\)），例子：\(\{aa,baa,cba,dba,eba\}\)，答案应该为 \(11\)。

代码

#include<bits/stdc++.h>
using namespace std;

#define int long long
const int N = 1e5 + 5, M = 510005, C = 26;
int n, t[M][C], tot = 1, siz[N], f[N], a[M];
string s[N];
vector<int> to[N]; 

inline int ins(string s, int pos){
	int len = s.size(), u = 1, lst = n + 1;
	for(int i = 0; i < len; ++i){
		int c = s[i] - 'a';
		if(a[u]) lst = a[u];
		if(!t[u][c]) t[u][c] = ++tot; 
		u = t[u][c];
	}
	a[u] = pos;
	return lst;
}
inline bool cmp(int A, int B) {return siz[A] < siz[B];}
inline bool cmpp(string A, string B) {return A.size() < B.size();}
inline void dfs(int u){
	vector<int> son; 
	for(auto v : to[u]) dfs(v), son.push_back(v);
	sort(son.begin(), son.end(), cmp);
	for(auto v : son){
		f[u] += siz[u] + f[v];
		siz[u] += siz[v];
	}
	++f[u], ++siz[u];
}
signed main(){
	cin >> n, a[1] = n + 1;
	for(int i = 1; i <= n; ++i) cin >> s[i], reverse(s[i].begin(), s[i].end());
	sort(s + 1, s + 1 + n, cmpp);
	for(int i = 1; i <= n; ++i) to[ins(s[i], i)].push_back(i);  
	dfs(n + 1);	
	cout << f[n + 1] - 1;
	return 0;
}