[dp优化] [矩阵加速递推] CF506E Mr- Kitayuta's Gift

posted on 2025-04-02 07:49:49 | under | source

题意：求在字符串 \(S\) 中插入 \(n\) 个字符使得 \(S\) 回文的方案数。一种方案不同当且仅当最终串不同。\(|S|\le 2\times 10^2,n\le 10^9\)。

记最终串是 \(T\)。条件为 \(S\) 是 \(T\) 的子序列。

\(T\) 长度是固定为 \(K=|S|+n\)，那么我们考虑从两端开始向中心填写字符，并实时维护匹配情况。有朴素 dp，记 \(f_{i,j,k}\) 为填到第 \(k\) 轮，还剩 \([i,j]\) 未匹配的方案数。转移如下：

• \(S_i=S_j\)：\(f_{i,j,k}\to f_{i+1,j-1,k+1}\)，\(f_{i,j,k}\times 25 \to f_{i,j,k+1}\)。
• \(S_i\ne S_j\)：\(f_{i,j,k}\to f_{i+1,j,k+1}\)，\(f_{i,j,k}\to f_{i,j-1,k+1}\)，\(f_{i,j,k}\times 24\to f_{i,j,k+1}\)。
• 此外，若 \(i>j\) 即匹配完毕：\(f_{i,j,k}\times 26\to f_{i,j,k+1}\)。

注意，若 \(2\nmid K\) 则在最后一步转移有特判。接下来先讨论 \(2\mid K\)。

即使矩阵加速还是过不去。注意到绝大多数转移都是自己转移到自己，考虑将转移放在自动机上，观察其特征。贺一张图：

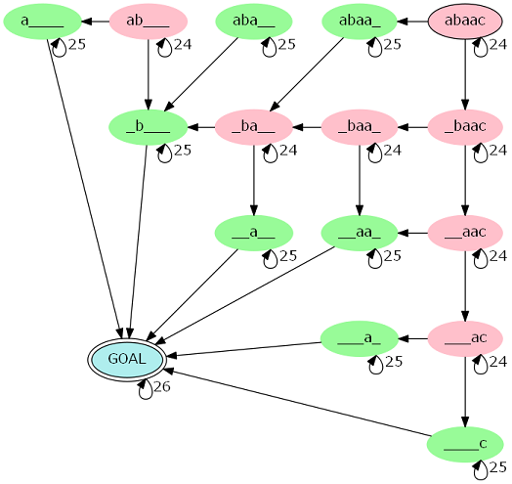
这样计算方案：先拎起一条路径（无自环），然后插入自环，最后相乘即可。自环只有三种，\(S_i\ne S_j\)（红点）、\(S_i= S_j\)（绿点）以及终点。

发现插入自环的方案数仅和红点绿点个数有关，记为 \((a,b)\)。那么答案即为 \(\sum f_{a,b}\times g_{a,b}\)，\(f_{a,b}\) 为 \((a,b)\) 路径个数，\(g_{a,b}\) 为在 \((a,b)\) 路径上插入自环的方案数的。

对于在状态 \([i,j]\) 截止的路径，有 \(b=\lceil \frac {K-(j-i+1)-a}{2}\rceil\)，所以 \((a,b)\) 实际上有 \(O(K)\) 种。那么 \(f\) 容易 dp 计算，\(O(K^3)\)。

对于 \(g\)，也许可以用多项式科技做，但是不优。朴素想法是再建一个自动机，然后矩阵加速。每个 \((a,b)\) 都要重新建，\(O(K^4\log n)\) 过不去。

矩阵加速可以计算出任意起终点走限定步的方案。那么实际上可以把它们压缩起来：

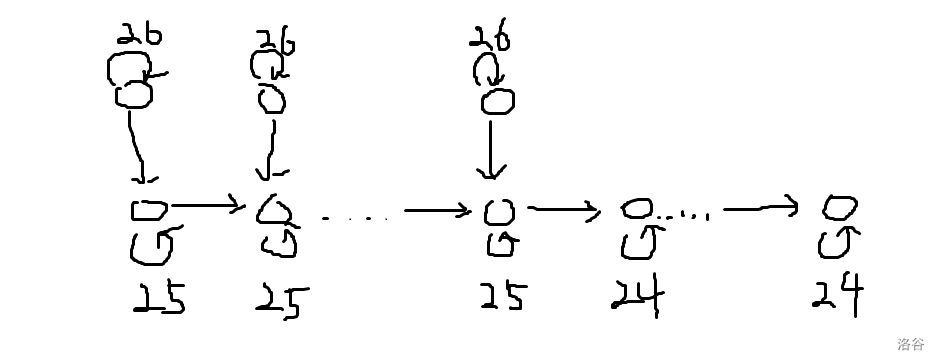
这样适当选取起终点即可得到 \((a,b)\)。只用算一次矩乘，\(O(K^3\log n)\)。

最后是 \(2\nmid K\)，那么就是不能最后一步从 \([i,i+1]\) 转移到终态。减去不合法的即可。此时 \(g_{a,b}\) 唯一的区别是不能走 \(26\) 自环，那我从 \(25\) 自环开始即可，相应的也要少走一步。

卡常：矩阵钦定从小的转移到大的，那么上三角矩阵 \(\frac 16\) 常数。

代码

#include<bits/stdc++.h>
using namespace std;

#define ADD(a, b) a = (a + b) % mod
#define val(x, y) (((x) <= (y)) && (c[x] ^ c[y]))
const int N = 2e2 + 5, M = 4e2, mod = 1e4 + 7;
int len, n, f[N][N][N], g[N], ans;
char c[N];

struct Matrix{
	int x, a[M][M];
	inline Matrix () {memset(a, 0, sizeof a);}
	inline Matrix operator * (const Matrix &A) const{
		Matrix C;
		for(int i = 1; i < M; ++i)
			for(int j = i; j < M; ++j)
				for(int k = i; k <= j; ++k)
					ADD(C.a[i][j], a[i][k] * A.a[k][j] % mod);
		return C;
	}
} I, P, Q;
inline Matrix qstp(Matrix A, int k) {Matrix res = I; for(; k; k >>= 1, A = A * A) if(k & 1) res = res * A; return res;}
inline int get(int x, int y) {return Q.a[101 - y][x + 200];}
inline int get2(int x, int y) {return Q.a[201 - y][x + 200];}
signed main(){
	for(int i = 1; i < M; ++i) I.a[i][i] = 1;
	for(int i = 1; i <= 100; ++i) P.a[i][i] = 26, P.a[i + 100][i + 100] = 25, P.a[i][i + 100] = 1;
	for(int i = 201; i < 400; ++i) P.a[i][i] = 24;
	for(int i = 101; i < 399; ++i) P.a[i][i + 1] = 1;
	
	scanf("%s%d", c + 1, &n), len = strlen(c + 1), n += len;
	f[1][len][0] = 1;
	for(int siz = len, j; siz; --siz)
		for(int i = 1; i + siz - 1 <= len; ++i){
			j = i + siz - 1;
			for(int a = 0, b; a <= len; ++a){	
				if(!f[i][j][a]) continue;
				b = (len - siz - a) / 2;
				if(c[i] == c[j]) ADD(f[i + 1][j - 1][a + val(i, j)], f[i][j][a]);
				else{
					ADD(f[i + 1][j][a + val(i, j)], f[i][j][a]);
					ADD(f[i][j - 1][a + val(i, j)], f[i][j][a]);
				}
			}
		}
	for(int i = 1; i <= len + 1; ++i)
		for(int j = 0; j < i; ++j)
			for(int a = 0; a <= len; ++a) ADD(g[a], f[i][j][a]);
	Q = qstp(P, (n + 1) / 2 - 1); 
	if(n & 1){
		for(int i = 1; i < len; ++i)
			if(c[i] == c[i + 1])
				for(int a = 0; a <= len; ++a)
					if(f[i][i + 1][a]) 
						ADD(ans, (mod - 1) * f[i][i + 1][a] % mod * get2(a, (len - 2 - a) / 2 + 1) % mod);
	}
	Q = Q * P;
	for(int a = 0; a <= len; ++a) ADD(ans, g[a] * get(a, (len - a + 1) / 2) % mod);
	cout << ans;
	return 0;
}