[CSPS 2019] [重心] [树形数据结构] [容斥] 树的重心

posted on 2023-08-25 09:02:09 | under 题集 | source

题意

给定一棵 \(n\) 个点的树 \(T\)。将该树的任意一条边断开后，可得到两棵新的分裂子树，求分别断开每条边后所得子树的重心编号之和。

思路

在此之前，大家应知道重心的判断式：对于任意 \(u\in T\)，都满足 \(siz_u\le \frac {|T|}2\)。

直观做法：遍历所有边，累加断开后两部分的重心编号。

显然复杂度为 \(O(n^2)\) 不可过，那不妨换个角度从点出发，计算有多少条边断开后使得该点为重心，定义 \(i\) 的合法断边的数量为 \(cnt_i\)，答案即为 \(\sum cnt_i*i\)。

但是我们还是没有头绪，如何快速计算出 \(cnt_i\) 呢？按照 CCF 的出题风格可知，不知道咋做时不妨挖掘性质。

• 一个性质

  令该树的一个重心 \(rt\) 为根（这样可以有较好的性质），则：对于 \(u\ne rt\)，\(u\) 的合法断边一定不在 \(u\) 的子树中。

  证明：

  如果断边在 \(u\) 的子树中，那么将 \(u\) 定为新根后，\(u\) 一定存在一棵子树 \(P\)，如下图所示：

  

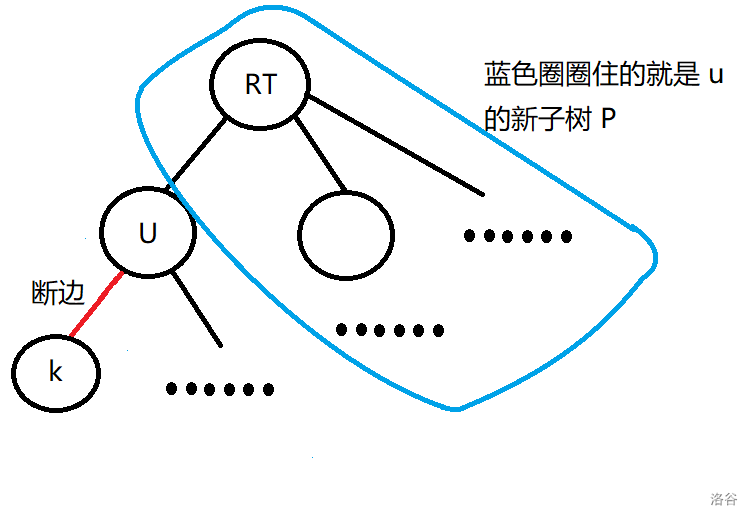
  又因为 \(rt\) 为重心，所以定义除 \(u\) 外 \(rt\) 的所有子节点为 \(v_i\)，则有 \(|P|=\sum siz_{v_i}\ge \frac n2 > \frac {n-siz_k}2\)，显然不满足重心的定义，证毕。

• \(x=rt\) 时的情况

  对于 \(x=rt\)，我们无论怎么割我们都只关注其最大子树 \(ma_1\) 和次大子树 \(ma_2\)，所以对割边的位置进行分类讨论：

  1. 割边 \((x,y)\) 在 \(ma1\) 中：

     同时满足 \(2*(siz_{ma1}-siz_y)\le n-siz_y\) 和 \(2*siz_{ma2}\le n-siz_y\)，取最大即可。

  2. 割边 \((x,y)\) 在 \(ma2\) 中：

     满足 \(2*siz_{ma1}\le n-siz_y\) 即可。

  \(\rm DFS\) 时顺便处理即可，这不是难点，接下来讨论 \(u\ne rt\) 的情况。

• \(x\ne rt\) 时的情况

  首先约定另一棵分裂子树的大小为 \(S\)，\(g_u\) 为 \(\max siz_v|v\in u,v\ne u\)。

  \(u\) 所在分裂子树被 \(u\) 分为两部分，若令 \(S\) 为另外一棵分裂子树，则这两部分为 \(n-S-siz_u\)、\(g_u\)。

  因为 \(u\) 为重心，所以有：

  \[\begin{cases} n-S-siz_u\le \frac {n-S}2 \\ g_u\le \frac {n-S}2 \end{cases}\]

  化简得： \(n-2*g_u\le S\le n-2*siz_u\)

• 算法实现

  于是目标就很明确了，对于 \(u\) 而言的合法割边需满足：

  1. \(n-2*g_u\le S\le n-2*siz_u\)。
  2. 割边不在 \(u\) 的子树中。

  只有 \(1\) 的话在 \(\rm DFS\) 过程中维护一个权值线段树 \(t\) 即可，求 \(cnt_u\) 就相当于一次区间查询。

  对于 \(2\)，线段树合并肯定能做但没必要。考虑容斥，再定义一个权值线段树 \(t2\)，由于 \(\rm DFS\) 过程中一定是先访问 \(u\) 再访问其子树，所以在访问其子树前 \(t2\) 中并没有 \(u\) 子树的贡献，而访问后就有了，利用这一点做差即可。

  （不用线段树合并的话，就可以用权值树状数组代替权值线段树）

  值得注意的是，同一条边 \((x,y)\) 对于不同的点而言会产生不同的 \(S\)，在边上方的点的 \(S\) 是 \(siz_y\)，而在下方的点的 \(S\) 是 \(n-siz_y\)。

  那么需要一个初始化：for(int i=1; i<=n;i++) t1.upd(siz[i],1);

  意思就是先默认所有边的贡献都是点在其上方时产生的，于是 \(S\) 就是 \(siz_i\)。

  这样做显然不对，会漏掉点在边下方的情况，因此在 \(\rm DFS\) 时还要加上 \(S=n-siz_u\) 的情况，代码长这样：t1.upd(n-siz[u],1);

  接着就是容斥数组 \(t2\) 了。事实上，我们并不在意 \(t2\) 的具体值，我们只关注遍历子树前后 \(t2\) 的变化值，变化值就是不满足 \(2\) 的割边数。于是在遍历前、计算贡献前（不然做不了容斥）加上 t2.upd(siz[u],1); 就可达到我们想要的效果了。

  不过这样做还是会算进不合法情况的，因为对于 \((x,y)\) 在 \(u\) 上方、且对应 \(S=siz_y\) 时的情况没有被去掉（容斥只能去掉 \((x,y)\) 在 \(u\) 下方的情况），想不算它也很简单，加上 t1.upd(siz[u],-1); 即可。

  还有一点：遍历完 \(u\) 的子树后，我们将处理与 \(u\) 同深的其它点 \(v_i\)，而在对于 \(u\) 子树的不合法方案放在 \(v_i\) 中可能就合法了（因为对于边的相对位置改变），也就是 t1.upd(siz[u],-1); 所删去的方案；同理对于 \(u\) 子树的合法方案放在 \(v_i\) 中可能不合法，也就是 t1.upd(n-siz[u],1); 所加上的方案。（直接听我讲很模糊，但在纸上模拟就比较清晰了）

  所以做完容斥后还需补上 t1.upd(siz[u],1),t1.upd(n-siz[u],-1);

代码实现

所以步骤就是：找重心定根 \(\to\) 建新树并预处理 \(\to\) 在做一次 \(\rm DFS\) 算贡献。

还有血的教训：

1. \(S\) 可能为 \(0\)，树状数组部分需要向右偏移 \(1\)。

2. 不要忘了初始化。

已经讲得差不多了，就不加注释咯。

#include<bits/stdc++.h>
using namespace std;

#define int long long
const int N=3e5+5;
int t,n,u,v,tot,head[N];
int rt,siz[N],g[N],p[N],ans,ma1,ma2,f[N];
struct qxx{
	int v,nxt;
}e[N<<1];
struct tree{
	int t[N];
	inline void clr() {for(int i=0;i<=N-5;i++){t[i]=0;}}
	inline int lowbit(int a) {return a&-a;}
	inline void upd(int a,int k) {a++;while(a<=n+1){t[a]+=k;a+=lowbit(a);}}
	inline int qry(int a) {a++;int res=0;while(a){res+=t[a];a-=lowbit(a);}return res;}
	inline int get(int l,int r) {return qry(max(r,0LL))-qry(max(l-1,0LL));}
}t1,t2;

inline void add(int u,int v){
	e[++tot]={v,head[u]};
	head[u]=tot;
}
inline void find_rt(int u,int fa){
	bool flag=1;
	siz[u]=1;
	for(int i=head[u]; i;i=e[i].nxt){
		if(e[i].v^fa){
			find_rt(e[i].v,u);
			siz[u]+=siz[e[i].v];
			if(siz[e[i].v]>n/2) flag=0;
		}
	}
	if(n-siz[u]<=n/2&&flag) rt=u;
} 
inline void dfs(int u,int fa){
	siz[u]=1; g[u]=0;
	for(int i=head[u]; i;i=e[i].nxt){
		if(e[i].v^fa){
			dfs(e[i].v,u);
			g[u]=max(g[u],siz[e[i].v]);
			siz[u]+=siz[e[i].v];
		}
	}
} 
inline void find_fir_sec(){
	ma1=-1; ma2=-1;
	for(int i=head[rt]; i;i=e[i].nxt){
		if(siz[e[i].v]>=siz[ma1]){
			ma2=ma1; 
			ma1=e[i].v; 
		} 
		else{ 
			if(siz[e[i].v]>=siz[ma2]){ 
				ma2=e[i].v;
			} 
		} 
	} 
} 
inline void dfs2(int u,int fa){ 
	t1.upd(siz[u],-1); t1.upd(n-siz[u],1); t2.upd(siz[u],1); 
	if(fa==ma1||f[fa]==1){
		f[u]=1;
	}
	if(u^rt){ 
		ans+=u*t1.get(n-siz[u]*2,n-g[u]*2); 
		ans+=u*t2.get(n-siz[u]*2,n-g[u]*2); 
		if(f[u]==1){
			if(2*max(siz[ma1]-siz[u],siz[ma2])<=n-siz[u]) ans+=rt;
		}
		else{
			if(u^ma1&&2*siz[ma1]<=n-siz[u]) ans+=rt;
			if(u==ma1&&2*siz[ma2]<=n-siz[ma1]) ans+=rt;
		}
	} 
	for(int i=head[u]; i;i=e[i].nxt){ 
		if(e[i].v^fa){ 
			dfs2(e[i].v,u);	
		}	
	}
	if(u^rt){
		ans-=u*t2.get(n-siz[u]*2,n-g[u]*2);
	}
	t1.upd(siz[u],1); t1.upd(n-siz[u],-1);
}
signed main(){
	cin>>t;
	while(t--){
		memset(head,0,sizeof head);
		memset(f,0,sizeof f);
		rt=0; ans=0; tot=0;
		t1.clr(); t2.clr();
		
		cin>>n;
		for(int i=1; i<n;i++){
			scanf("%lld%lld",&u,&v);
			add(u,v); add(v,u);
		}
		find_rt(1,0);
		dfs(rt,0);
		find_fir_sec();
		
		for(int i=1; i<=n;i++) t1.upd(siz[i],1);
		dfs2(rt,0);
		printf("%lld\n",ans);
	}
	return 0;
}