Treap笔记(随笔)
今天来写一下 \(treap\) 笔记,本文章大部分内容来自OI Wiki
二叉搜索树(简称BST)
定义:
对于一棵树里的所有根,它的左子树上所有点的附加值小于根节点,右子树上所有点的附加值大于根节点
空树也是二叉搜索树
性质:
1.二叉树的中序遍历的权值序列是不降的
2.一颗有 \(n\) 个节点的二叉搜索树,它的最大深度为 \(n\),最小深度为 \(logn\) 构造一颗二叉搜索树的期望高度是 \(logn\)(为什么?)
功能:
以下 root 指以 root 为根的二叉搜索树,树指二叉搜索树
1.查找最大/最小值:最大值是右链顶点,最小值是左链顶点
2.搜索元素:若值大于 root 去左搜,反之去右,直到找到相等的值
3.插入元素:
若 root 为空,直接返回一个值为 value 的新节点
等于,该节点的附加域该值出现的次数自增 1
大于去左插入,小于去右
4.删除元素:
先搜索该节点,若附加域不为 1 减 1 即可,如果为 1
若 root 为叶子节点,则直接删除即可
若为链节点,返回儿子
若有两个儿子,依树而定
5.求元素排名:
排名定义为将数组元素升序排序后第一个相同元素之前的数的个数加一
查找一个元素的排名,先查找元素,查找过程中若向右跳,答案加上左儿子节点个数加当前节点重复的数个数,最后答案加上终点的左儿子子树大小加一
6.找排名第 k 的元素:
若其左子树的大小大于等于 k ,则该元素在左子树中;
若其左子树的大小在区间[k-count,k-1]为当前结点的值的出现次数)中,则该元素为子树的根节点;
若其左子树的大小小于k-count,则该元素在右子树中。
以上操作的时间均为 \(O(h)\),具体插入与删除依据树的种类为定
平衡树
前面说过,二叉搜索树在某种情况下高度会退化为O(n),时间就也会退化为O(n),这是我们不能接受的,所以我们需要平衡树来进行平衡操作
定义:通过平衡操作优化二叉搜索树的深度以优化操作时间的二叉搜索树
平衡树有很多种比如$ Treap,Splay,AVL$ 还有机房神犇独爱的替罪羊树
所以我们着重讲一下 \(Treap\)
Treap
\(treap\) 通过给每个节点赋予两个节点 \(key\) 和 \(val\) 来使BST尽量随机在每一个点插入的时候(其中\(key\)是给定的)都赋一个随机\(val\)值,使树同时满足堆与BST的性质,给出一幅图来阐明堆如何优化BST的深度(以大根堆为例)
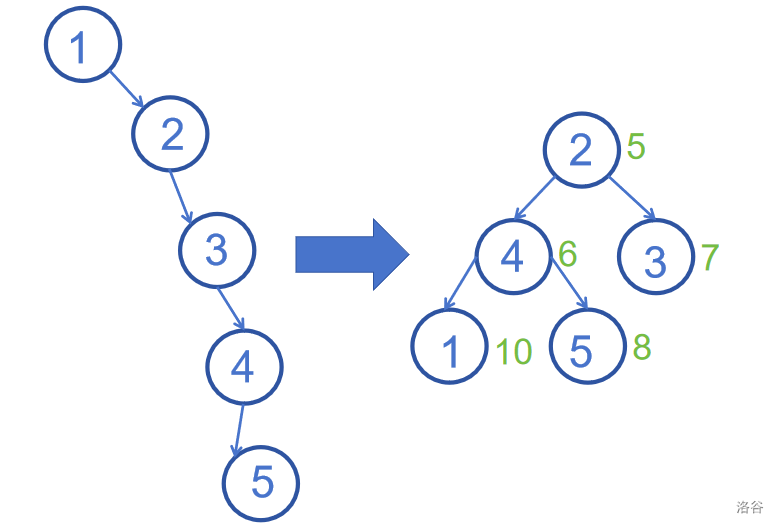
如图所示,若我们将键值为\(1,2,3,4,5\) 的序列依次加入BST,则是左边的链,右边则是一种可能的随机堆优化
时间复杂度
不会证
直接给结论:设树高为 \(n\) 那么每个节点的期望高度都是 \(log n\),所以 Treap 的操作的期望复杂度也都是 \(O(log n)\)
有旋Treap
给 treap 插入新节点时,需要同时维护树和堆的性质。其中,二叉搜索树的性质可以在插入时维护,而堆性质的维护则有两种处理方法,分别是旋转和分裂、合并。使用这两种方法的 treap 被分别称为 旋转 treap 和 无旋 treap,这篇文章主要讲有旋Treap
create操作:
首先我们需要建树,对于一棵 Treap 它要存储的元素有:
struct Tree{
int l,r;//左右儿子
int key;//键值
int val;//堆值
int idx;//计数器
int siz;//子树大小
}
接下来建树,为了处理边界,我们需要两个“哨兵”节点,权值 \(key\) 分别为正无穷和负无穷,添加节点操作是
int cnt;
int create(int key){
tr[++cnt].key=key;
tr[cnt].val=rand();//随机赋值
tr[cnt].idx=1;
tr[cnt].siz=1;//现在我们默认的是创建叶节点
return cnt;
}
以及为了上传子树大小等信息,我们要像线段树一样 pushup
void pushup(int u){
tr[u].siz=tr[tr[u].l].siz+tr[tr[u].r].siz+tr[u].idx;
......
}
那么初始操作建树就是
void build(){
create(-INF),create(INF);
root=1;
tr[1].r=2;
pushup(root);
//要是随机值不符合堆的性质后面进行调整
}
旋转操作:
通过前面可以知道,我们要维护一棵二叉搜索树的平衡有很多操作,比如现在讲的旋转操作
旋转分左旋和右旋,先看旋转后树会发生什么改变:
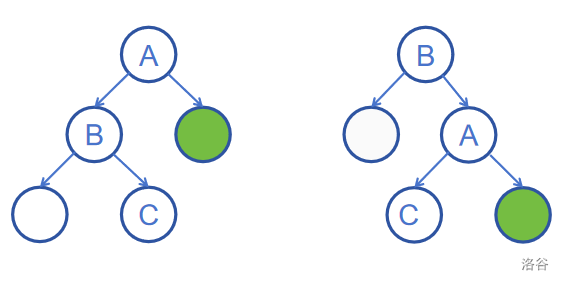
我们可以看到,从左往右,在旋转后,进行的操作是:
1.将A的左儿子向右上旋转,替代A成为根节点
2.A向右下旋转,成为B的右子树
3.B的右子树成为A的左子树
从左向右就是右旋,从右向左就是左旋,具体怎么旋转需要进行判断
void zig(int &u){//右旋
int kl=tr[u].l;//开变量暂存
tr[u].l=tr[kl].r;//第三步
tr[kl].r=u;//第二步
u=kl;//第一步,要最后执行,因为前面要用到 u
pushup(tr[u].r),pushup(u);
}
void zag(int &u){//左旋
//和右旋完全镜像
int kr=tr[u].r;
tr[u].r=tr[kr].l;
tr[kr].l=u;
u=kr;
pushup(tr[u].l),pushup(u);
}
插入操作:
我们锚定通过一些左右旋操作使该节点一定成为叶子节点,然后从根节点出发,按照BST的性质,大了往左,小了往右,若与当前节点值相同,\(idx\) 计数器加一,每往下搜一层,若进入左子树,左子树的左儿子的 val 比该节点的值大,就右旋,进入右子树,其右儿子的 val 比该节点大,那么就左旋,代码如下:
void insert(int &u,int key){
if(!u) u=create(key);
else{
if(tr[u].key==key) tr[u].idx++;
else if(tr[u].key>key){//向左
insert(tr[u].l,key);
if(tr[tr[u].l].val > tr[u].val) zig(u);//右旋
}
else{//右
insert(tr[u].r, key);
if(tr[tr[u].r].val > tr[u].val) zag(u);//左旋
}
}
pushup(u);
}
删除操作:
叶子节点显而易见可以直接删除,若节点的计数器 idx 不为 1 也可以直接减 1,若为 1 ,
就要分情况判断,具体看代码
void del(int &u,int key){
if(!u) return ;//不存在;
else{
if(tr[u].key==key){
if(tr[u].idx>1) tr[u].idx--;
else{
if(tr[u].l||tr[u].r){
if(!tr[u].r||tr[tr[u].l].val>tr[tr[u].r].val){
zig(u);//右旋
del(tr[u].r,key);//右旋使 u 成为根的右子树
}
else{
zag(u);//左旋
del(tr[u].l,key);
}
}
else{
u=0;
}
}
}
else{
if(tr[u].key>key) del(tr[u].l,key);
else del(tr[u].r,key);
}
}
//最后别忘了pushup
pushup(u);
}
接下来就是一些Treap具体的作用,P3369 模板 普通平衡树
懒得讲了可以看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
const int INF=1e8;
struct Tree{
int l,r;//左右儿子
int key;//键值
int val;//堆值
int idx;//计数器
int siz;//子树大小
}tr[N];
int cnt;
int create(int key){
tr[++cnt].key=key;
tr[cnt].val=rand();//随机赋值
tr[cnt].idx=1;
tr[cnt].siz=1;//现在我们默认的是创建叶节点
return cnt;
}
void pushup(int u){
tr[u].siz=tr[tr[u].l].siz+tr[tr[u].r].siz+tr[u].idx;
}
int root;
void build(){
create(-INF),create(INF);
root=1;
tr[1].r=2;
pushup(root);
//要是随机值不符合堆的性质后面进行调整
}
void zig(int &u){//右旋
int kl=tr[u].l;//开变量暂存
tr[u].l=tr[kl].r;//第三步
tr[kl].r=u;//第二步
u=kl;//第一步,要最后执行,因为前面要用到 u
pushup(tr[u].r),pushup(u);
}
void zag(int &u){//左旋
//和右旋完全镜像
int kr=tr[u].r;
tr[u].r=tr[kr].l;
tr[kr].l=u;
u=kr;
pushup(tr[u].l),pushup(u);
}
void insert(int &u,int key){
if(!u) u=create(key);
else{
if(tr[u].key==key) tr[u].idx++;
else if(tr[u].key>key){//向左
insert(tr[u].l,key);
if(tr[tr[u].l].val>tr[u].val) zig(u);//右旋
}
else{//右
insert(tr[u].r, key);
if(tr[tr[u].r].val>tr[u].val) zag(u);//左旋
}
}
pushup(u);
}
void del(int &u,int key){
if(!u) return ;//不存在;
else{
if(tr[u].key==key){
if(tr[u].idx>1) tr[u].idx--;
else{
if(tr[u].l||tr[u].r){
if(!tr[u].r||tr[tr[u].l].val>tr[tr[u].r].val){
zig(u);//右旋
del(tr[u].r,key);//右旋使 u 成为根的右子树
}
else{
zag(u);//左旋
del(tr[u].l,key);
}
}
else{
u=0;
}
}
}
else{
if(tr[u].key>key) del(tr[u].l,key);
else del(tr[u].r,key);
}
}
//最后别忘了pushup
pushup(u);
}
int qrank(int u,int x){
if(!u) return 1;
else{
if(tr[u].key==x) return tr[tr[u].l].siz+1;
else if(tr[u].key>x) return qrank(tr[u].l,x);
else return tr[tr[u].l].siz+tr[u].idx+qrank(tr[u].r,x);
}
}
int qkey(int u,int x){
if(!u) return INF;
else{
if(tr[tr[u].l].siz>=x) return qkey(tr[u].l,x);
else if(tr[tr[u].l].siz+tr[u].idx>=x) return tr[u].key;
else return qkey(tr[u].r,x-tr[tr[u].l].siz-tr[u].idx);//减去左子树和根节点的权值
}
}
int qpre(int u,int x){
if(!u) return -INF;
else{
if(tr[u].key>=x) return qpre(tr[u].l,x);//被左子树包含
return max(tr[u].key,qpre(tr[u].r,x));
}
}
int qnxt(int u,int x){//与前驱同理
if(!u) return INF;
else{
if(tr[u].key<=x) return qnxt(tr[u].r,x);
return min(tr[u].key,qnxt(tr[u].l,x));
}
}
int T;
int main(){
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
build();
cin>>T;
while(T--){
int op,x;
cin>>op>>x;
if(op==1) insert(root,x);
if(op==2) del(root,x);
if(op==3) cout<<qrank(root,x)-1<<endl;//由于有哨兵,所以要减一
if(op==4) cout<<qkey(root,x+1)<<endl;//和上面同理
if(op==5) cout<<qpre(root,x)<<endl;
if(op==6) cout<<qnxt(root,x)<<endl;
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号