树链剖分随笔

声明：本题解仅供个人参考，具有不严谨，不全面等问题

本文大多数内容来自OI Wiki

树链剖分有多种，比如重链剖分，长链剖分，这两者的区别在于对重儿子的定义不同。

树链剖分，顾名思义，就是把树剖成链来解决问题。

以什么方式把树剖成链？接下来我们看一些定义：

重链剖分

重子节点： 表示其子节点中子树最大的子结点。如果有多个，取其一。如果没有子节点，就无重子节点。

轻子节点： 表示剩余的所有子结点。

重边： 从一个结点到重子节点的边。

轻边： 其他的边。

重链：若干条首尾衔接的重边以及重边所连的点构成的链，单独的点也为重链。

引用OI Wiki 的图

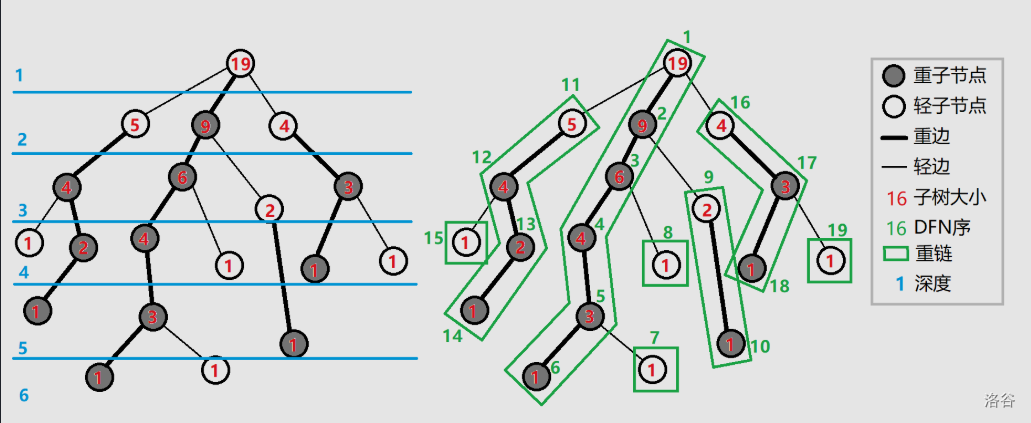
性质：

1.每一个节点必定属于且仅属于一条重链

2.重链开头的结点不一定是重子节点（图中所示）

3.重链完全剖分整棵树

4.一条链中的DFS序是连续的（重点！！！这是为什么线段树能维护的原因）

了解了这些，我们来看看具体运用

P3178 树上操作 - 洛谷

树上修改问题，完完全全可以只看代码读懂这道题。

在这道题中，我们的线段树完全是按最常规的方式所建(维护连续区间和)，只在查询操作中产生了改变，以链为单位进行答案的累加，由于链中的编号是连续的，所以线段树可以直接一次查出链中所有节点和，代码注释很全，有问题看代码。

#include<bits/stdc++.h>
#define int long long  
using namespace std;
const int N=1e6+10;
int n,m;
int a[N],w[N];
struct Edge{
	int to;
	int next;
}e[N<<1];
int h[N];
int cnt;
void add(int a,int b){
	e[cnt].to=b;
	e[cnt].next=h[a];
	h[a]=cnt++;
	return ;
}
int dep[N];
int siz[N];
int fa[N];
int son[N];//该节点的重儿子 
void dfs1(int u){
	son[u]=-1;//初始先赋值为 -1 后面覆盖，没有的也不用特判 
	siz[u]=1; //自己的大小 
	for(int i=h[u];~i;i=e[i].next){
		int v=e[i].to;
		if(v==fa[u]) continue;
		if(!dep[v]){//使用 dep 代替 vis  
			dep[v]=dep[u]+1;
			fa[v]=u;
			dfs1(v);
			siz[u]+=siz[v];//遍历完后再从子树加到父亲 
			 if(son[u]==-1||siz[v]>siz[son[u]]){
			 	son[u]=v;//筛选重儿子 
			 }
		}
	} 
}
int idx;
int top[N];//该节点所在重链顶部 
int dfn[N];//dfs序 
int id[N];//dfs序的节点编号 
void dfs2(int u,int t){
	top[u]=t;//初始是dfs2(1,1)：根所在的重链顶部一定是它本身 
	idx++;//累加 dfs 序
	dfn[u]=idx;
	id[idx]=u;
	a[idx]=w[u];
	if(son[u]==-1){//没有重儿子说明没有儿子 
		return ;
	}
	dfs2(son[u],t); //一条重链里的点都是以 t 为顶部 
	for(int i=h[u];~i;i=e[i].next){
		int v=e[i].to;
		if(v!=son[u]&&v!=fa[u]){
			dfs2(v,v);//由一条链进入另一条链一定从顶部进入 
		}
	} 
}
struct SG{
	int l,r;
	int sum;
	int lazy;
}tr[N<<2];
void pushup(int u){
	tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
} 
void pushdown(int u){
	int l=(u<<1);
	int r=(u<<1|1);
	tr[l].sum+=tr[u].lazy*(tr[l].r-tr[l].l+1);
	tr[r].sum+=tr[u].lazy*(tr[r].r-tr[r].l+1);
	tr[l].lazy+=tr[u].lazy;
	tr[r].lazy+=tr[u].lazy;
	tr[u].lazy=0;
}
void build(int u,int l,int r){
	tr[u].l=l;
	tr[u].r=r;
	if(l==r){
		tr[u].sum=a[l];
		return ;
	}
	int mid=l+r>>1;
	build(u<<1,l,mid);
	build(u<<1|1,mid+1,r);
	pushup(u);
}
void modify1(int u,int x,int val){
	if(tr[u].l==tr[u].r){
		tr[u].sum+=val;
		return ;
	}
	pushdown(u);
	int mid=tr[u].l+tr[u].r>>1;
	if(x<=mid){
		modify1(u<<1,x,val);
	}
	else{
		modify1(u<<1|1,x,val);
	}
	pushup(u);
}
void modify2(int u,int l,int r,int val){
	if(l<=tr[u].l&&r>=tr[u].r){
		tr[u].sum+=val*(tr[u].r-tr[u].l+1);
		tr[u].lazy+=val;
		return ;
	}
	//改到两个链之间/不连续的点的情况不会被 query() 访问  
	pushdown(u);
	int mid=tr[u].l+tr[u].r>>1;
	if(l<=mid) modify2(u<<1,l,r,val);
	if(r>mid) modify2(u<<1|1,l,r,val);
	pushup(u);
}
int sumup(int u,int l,int r){
	int res=0;
	if(l<=tr[u].l&&r>=tr[u].r){
		return tr[u].sum;
	}
	pushdown(u);
	int mid=tr[u].l+tr[u].r>>1;
	if(l<=mid){
		res+=sumup(u<<1,l,r);
	}
	if(r>mid){
		res+=sumup(u<<1|1,l,r);
	}
	return res;
} 
int query(int x,int y){
	int fx=top[x];
	int fy=top[y];
	int ans=0;
	//和跳LCA的过程是很像的
	while(fx!=fy){//不在同一条链中 
		//谁深谁往上跳 
		if(dep[fx]>=dep[fy]){
			ans+=sumup(1,dfn[fx],dfn[x]);//跳的过程中累加贡献 
			x=fa[fx];//链顶的父亲必定是属于新的链 
			fx=top[x];//新的链的链顶 
		}
		else{
			ans+=sumup(1,dfn[fy],dfn[y]);
			y=fa[fy];
			fy=top[y];
		}
	}
	if(dfn[x]<=dfn[y]){//同一条链中 
		ans+=sumup(1,dfn[x],dfn[y]);
	}
	else{
		ans+=sumup(1,dfn[y],dfn[x]);
	}
	return ans;
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);   cout.tie(0); 
	memset(h,-1,sizeof h);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>w[i];
	}
	for(int i=1;i<n;i++){
		int u,v;
		cin>>u>>v;
		add(u,v);
		add(v,u);
	}
	dfs1(1);
	dfs2(1,1);
	build(1,1,n);
	while(m--){
		int k;
		int x,y;
		cin>>k>>x;
		if(k==1){
			cin>>y;
			modify1(1,dfn[x],y);
		}
		else if(k==2){
			cin>>y;
			modify2(1,dfn[x],dfn[x]+siz[x]-1,y);
			//以根的dfs序加上子树大小就是dfs序最大的儿子 
		}
		else{
			cout<<query(1,x)<<endl;
		}
	}
	return 0;
}

在线段树合并模板中

P4556 雨天的尾巴 /(模板)_线段树合并 - 洛谷

也是树上问题，可以用树链剖分解决，AC完模板推荐写一下这道题（用树剖比线段树合并简单）