DP随笔
本蒟蒻动态规划实在是太蒻了,特此写一篇学习笔记
update:2024/11/26 :本来这个帖子所有的代码都是可展开的,本蒟蒻为了一己私欲,为了让帖子看起来更长,删除了这个功能
update:2025/1/20:腥的一年,DP太难了,排列组合也好难,遂AFO,于是缓缓,来 被迫 更新


简介
动态规划是一种将一个复杂问题分解为多个简单的子问题求解的方法。将子问题的答案存储在记忆数据结构中,当子问题再次需要解决时,只需查表查看结果,而不需要再次重复计算,因此节约了计算时间(good)
dp三条件 :
最优子结构,无后效性和子问题重叠
最优子结构:
1.证明问题最优解的第一的组分是做出选择
2.给定可获得的最优解的选择后,确定这次选择会产生哪些子问题,以及如何最好地刻画子问题空间
3.证明作为构成原问题最优解的组成部分,每个子问题的解就是它本身的最优解(应该就是无后效性的意思吧)
无后效性:
已经求解的子问题,不会再受到后续决策的影响
子问题重叠:
如果有大量的重叠子问题,我们可以用空间将这些子问题的解存储下来,避免重复求解相同的子问题,从而提升效率
dp三要素 :
状态定义,状态转移方程,初始状态
状态定义:
将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来,最简单的就是用数组来保存当前的每一个状态,这个状态就是每个子问题的决策
状态转移方程
当前状态与上一个状态之间的关系
初始状态
给出的状态转移方程是一个递推式,需要一个递推的终止条件或边界条件
基本思路
1.将原问题分成若干个阶段,每个阶段对应若干个子问题,提取这些子问题的特征(称为阶段)
2.寻找每个阶段可能的决策,或者说是各状态间的相互转移方式(用数学的语言描述就是 状态转移方程)
3.按一定顺序求解每一个阶段的问题
分类
dp大致可分为11种:记忆化搜索,线性DP,区间DP,背包DP,树形DP,状态压缩DP,数位DP,计数型DP,递推型DP,概率型DP,博弈型DP
记忆化搜索作为最先接触到的DP实现方式,让它成为讲解的开始吧
记忆化搜索
记忆化搜索是动态规划的一种实现方式,本质上就是DP,当算法需要计算某个子问题的结果时,它首先检查是否已经计算过该问题。如果已经计算过,则直接返回已经存储的结果;否则,计算该问题
例题
P1002 [NOIP2002 普及组] 过河卒
相信这道题大家很熟悉了(你谷门面)题意自己看,我们初学DP,对这到题使用了递推的思路,即这一个格子的步数为上面的格子加左边的格子的步数,现在看来二维数组\(i,j\)就是状态的表示,而递推的过程也就相当于状态转移,边界问题也就是初始状态,这就是最纯粹的DP啊(感叹),还是吧代码贴出来水长度吧,但我好像没用搜索?反正这道题可以记忆化搜索(根本没用)就是啦(╬▔皿▔)╯
#include<bits/stdc++.h>
using namespace std;
long long a[30][30];
int x[8]={2,1,-1,-2,-2,-1,1,2};
int y[8]={1,2,2,1,-1,-2,-2,-1};
int main(){
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
int n,m,p,q;
cin>>n>>m>>p>>q;
n+=2,m+=2,p+=2,q+=2;
for(int i=2;i<=n;i++){
for(int j=2;j<=m;j++){
a[i][j]=1;
}
}
a[p][q]=0;
for(int i=0;i<8;i++){
int x1=p+x[i];
int y1=q+y[i];
a[x1][y1]=0;
}
for(int i=2;i<=n;i++){
for(int j=2;j<=m;j++){
if(i==2&&j==2){
continue;
}
else if(a[i][j]==0){
continue;
}
else if(i==2){
a[i][j]=a[i][j-1];
}
else if(j==2){
a[i][j]=a[i-1][j];
}
else{
a[i][j]=a[i-1][j]+a[i][j-1];
}
}
}
cout<<a[n][m];
return 0;
}
再贴一道例题easy~
线性DP
线性动态规划是一种在线性结构上进行状态转移的动态规划方法。它的目标函数为特定变量的线性函数,约束是这些变量的线性不等式或等式,目的是求目标函数的最大值或最小值,如果状态包含多个维度,但是每个维度上都是线性划分的阶段,也属于线性 DP。比如背包问题、区间 DP、数位 DP 等都属于线性 DP。听上去不太拟人,会写就行
such as:B3637 最长上升子序列
这下知道是啥了吧
背包DP
线性DP的一种,嘛也是十分亲民拟人的DP,讲真有一段时间没写过了,种类有点多(写一半才发现怎么这么多QAQ),细讲一下,这一类题的定义应该不重要吧
0-1背包
最最最无脑背包
题意概要:有\(n\)个物品和一个容量为\(W\)的背包,每个物品有重量\(w_{i}\)和价值\(v_{i}\)两种属性,要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量
设DP状态\(f_{i,j}\)为在只能放前\(i\)个物品的情况下,容量为\(j\)的背包所能达到的最大总价值,最基础的转移就是
\(dp[i][j]=max(dp[i][j],dp[i][j-w[i]]+v[i])\)相信不用过多解释了————还是附个图吧
假设背包容量为\(8\),物品有\(4\)件
物品重量和价值如下

操作完后是这个样子
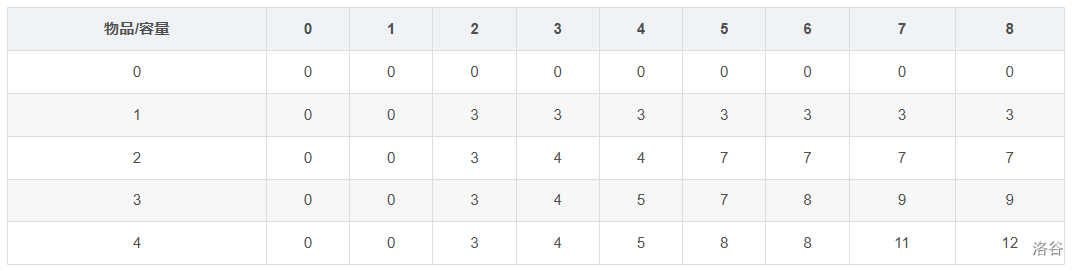
就这样了刚学OI都会了吧
二维还是太消耗脑细胞了直接压至一维\(f_{i}\)表示容量为\(i\)时的最大价值,\(f[j]=max(f[j],f[j-w[i]]+w[i])\)与上main的没什么区别
但不管是一维还是二维都要注意一个问题,那就是\(i,j\)的枚举顺序,先和OI Wiki一样贴份错误代码
for (int i = 1; i <= n; i++)
for (int j = 0; j <= W - w[i]; j++)
f[j + w[i]] = max(f[j] + v[i], f[j + v[i]]);
相信大家都知道\(j\)要逆序枚举,but why?(至少我忘了),很显然,如果这么去处理,枚举\(i\)时只要还有空间就可以放\(i\)(完全背包)
而我们只要逆序枚举\(j\)就不会出现\(i\)被选多次的情况,如果不太明白就自己画图手推一下
正确代码
for (int i = 1; i <= n; i++)
for (int j = W; j >= w[i]; j--) f[j] = max(f[j], f[j - w[i]] + v[i]);
update:2024/11/27:今天做了一个很新(我没写过这种)的\(0-1\)背包Knapsack 2
乍一看和模板背包没有any区别,但是我们一看数据范围,\(w=1e9\),如果拿重量当状态,很明显会爆掉,那么我们可以换一个思考方向,看到物品数和价值都很小,那么问题显而易见了,物品是我们压掉无人在意的状态。那么就只能用价值当状态了,所以我们设\(f_i\)为当前总价值为\(i\)时的最小重量,那么有转移方程\(f[j]=min\left (f[j],f[j-v[i]]+w[i] \right )\) 那么代码很好写啦(^-^)
#include<bits/stdc++.h>
#define int long long//记得开 long long 哦( •̀ω•́)
using namespace std;
const int N=1e5+10;
int n,m;
int v[N];
int w[N];
int sum;
int f[N];
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>w[i]>>v[i];
sum+=v[i];
}
memset(f,0x3f,sizeof f);
f[0]=0;
for(int i=1;i<=n;i++){
for(int j=sum;j>=v[i];j--){
f[j]=min(f[j],f[j-v[i]]+w[i]);
}
}
for(int j=sum;j;j--){
if(f[j]<=m){
cout<<j;
break;
}
}
return 0;
}
完全背包
完全背包模型与\(0-1\)背包类似,与\(0-1\)背包的区别仅在于一个物品可以选取无限次,而非仅能选取一次。
手推一下,刚刚已经说过\(j\)顺推就是完全背包的写法,那么与\(0-1\)背包相同,我们可以写出代码
for (int i = 1; i <= n; i++)
for (int j = w[i]; j <= W; j++)
if (f[j - w[i]] + v[i] > f[j]) f[j] = f[j - w[i]] + v[i]; // 核心状态方程
反正就一个样
懒的找例题P1616 疯狂的采药
多重背包
多重背包也是\(0-1\)背包的一个变式。与\(0-1\)背包的区别在于每种物品有\(k_i\)个,而非一个。不通过任何力气手段,暴力思考的话直接多加一层循环就可以了
for (int i = 1; i <= n; i++) {
for (int j = W; j >= w[i]; j--) {
//第i个物品选几个
for (int k = 1; k * w[i] <= j && k <= cnt[i]; k++) {
dp[j] = max(dp[j], dp[j - k * w[i]] + k * v[i]);
}
}
}
但这样时间复杂度有一点巨\(O\left (nm\sum_{n}^{i=1}\right)\),我们可以用倍增优化
for(int i=1;i<=n;i++){
int v,w,m;
cin>>v>>w>>m;//体积,价值和个数
int k=1;
while(k<=m){///将物品的1,2,4.....倍存进去
t[++cnt].v=v*k;
t[cnt].w=w*k;
m-=k;
k<<=1;
}
if(m){
t[++cnt].v=v*m;
t[cnt].w=w*m;
}
}
详见这篇帖子 A J 的学习笔记
例题:P1776 宝物筛选
混合背包
呐就是把上面三种背包结合了啦,我们只要写三个判断再把代码copy一下就行了,代码都不想写P1833 樱花
二维费用背包
就是有两维代价的背包,与相应的一维费用背包唯一的区别就是多了一维(废话)直接看代码就是了(以0-1背包为例)P1855 榨取kkksc03
for (int k = 1; k <= n; k++)
for (int i = m; i >= mi; i--) // 对经费进行一层枚举
for (int j = t; j >= ti; j--) // 对时间进行一层枚举
dp[i][j] = max(dp[i][j], dp[i - mi][j - ti] + 1);
依赖背包
将选父节点和选父节点和子节点的情况列为一组,抽象为分组背包(一组中最多选一个)就可以求解
其他
还有各种能抽象成背包的问题,读者可以自己研究
类似于拔河问题P1537 弹珠
区间DP
是线性DP的拓展,它在分阶段地划分问题时,与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系,具有三个特点
合并:即将两个或多个部分进行整合,当然也可以反过来
特征:能将问题分解为能两两合并的形式
求解:对整个问题设最优值,枚举合并点,将问题分解为左右两个部分,最后合并两个部分的最优值得到原问题的最优值
还是先贴一道题就知道是什么东东了P1880 [NOI1995] 石子合并 有没有想到果子合并呢,好像有关系又没关系,在写合并果子的时候我们有的是力气手段来维护最小的果子堆,但这里石子构成了环失去了力气手段,但是都把区间两个字拍你脸上了就考虑一下区间DP嘛
思路
我们先来考虑不构成环的情况:令\(f_{i,j}\)为将\(i,j\)区间内所有石子合并的最大值,那么有转移方程: \(f(i,j) = \max_{i \le k < j} \left\{ f(i,k) + f(k+1,j) + \sum_{t=i}^{j} a_t \right\}\) 求和可以用前缀和优化,我们以\(len=j-i+1\)作为 DP 的阶段。首先从小到大依次枚举\(len,i,j\)进行转移
至于最小值同理
环的处理
方法一:由于石子围成一个环,我们可以枚举分开的位置,将这个环转化成一个链,由于要枚举n次,,最终的时间复杂度为 \(O(n^4)\)
方法二:将链延长一倍,第\(i\)的位置与\(n+i\)相同最后取\(f(1,n),f(2,n+1),...,f(n,2n-1)\)的最优解时间复杂度\(O(n^3)\)
美丽代码:
for (len = 2; len <= n; len++)
for (i = 1; i <= 2 * n - len; i++) {
int j = len + i - 1;
for (k = i; k < j; k++)
f[i][j] = max(f[i][j], f[i][k] + f[k + 1][j] + sum[j] - sum[i - 1]);
}
关于环的处理,还可以看看这些题
update:2024/11/26 再也不说区间DP识别度高了P9119 [春季测试 2023] 圣诞树
这道题贪心竟然可以得\(75pts\)赞美西西弗~,那么我们来想想正解,首先需要知道一个性质:在连边时,不交叉始终比交叉优,至于证明,显然相信大家都会了,既然贪心不行我们就来设计DP状态吧,由于路径不交叉,所以我们遍历点时每次一定会落在顶点左边或右边最上面没有被遍历的点,否则就会漏点,后面再到它就会交叉路径,所以我们可以设$f_{i,j,k} \(表示从\)i+1\(到\)j-1$还没有遍历,在顶点的左边(k=0)或右边(k=1)时的距离,那么这就是一道区间DP,存每个点的时候,我们有
for(int i=k;i<=n;i++){
p[i-k]=i;
}
for(int i=1;i<=k;i++){
p[i+n-k]=i;
}
举例设\(n=12\),以\(6\)为顶点,\(p_{1,n}\)即为{\(7,8,9,10,11,12,1,2,3,4,5,6\)},倒序从\(6\)到\(1\)就是从右往下,正序从\(7\)到\(12\)是从左往下,如图:
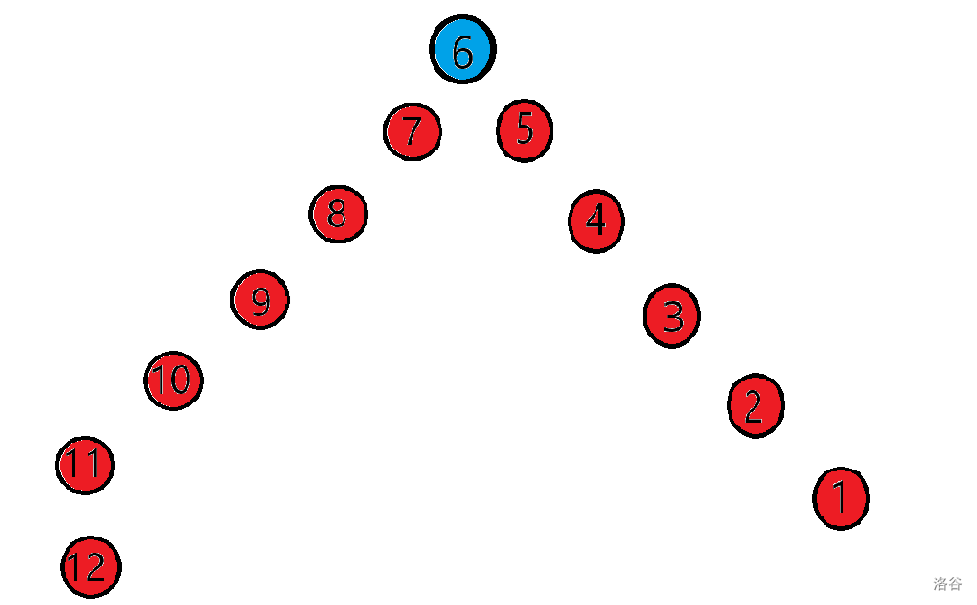
补药相信题的图片啊,被欺骗了,逆时针就该是这样没问题
转移的时候,我们以在左边的时候为例,转移方程就是\(f_{l,r,0} =min(f_{l−1,r,0} +dis(l−1,l),f _{l−1,r,1}+dis(l,r))\)那么右边同理
所以我们可以写出美丽代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e3+10;
const int INF=1e18;
int n;
double x[N],y[N];
int dp[N][N][2];
int g[N][N][2];
int p[2*N];
double q(int a,int b){
return sqrt(((x[a]-x[b])*(x[a]-x[b]))+((y[a]-y[b])*(y[a]-y[b])));
}
void as(int l,int r,int k){
if(l<0||r>n) return ;
if(k==0){
if(g[l][r][0]) as(l-1,r,1);
else as(l-1,r,0);
}
else{
if(g[l][r][1]) as(l,r+1,1);
else as(l,r+1,0);
}
cout<<(k?p[r]:p[l])<<" ";
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n;
int k;
int maxk=-INF;
for(int i=1;i<=n;i++){
cin>>x[i]>>y[i];
if(y[i]>maxk){
maxk=y[i];
k=i;
}
}
for(int i=k;i<=n;i++){
p[i-k]=i;
}
for(int i=1;i<=k;i++){
p[i+n-k]=i;
}
/*for(int i=1;i<=2*n;i++){
cout<<"i=="<<p[i]<<endl;
}*/
for(int l=0;l<=n;l++){
for(int r=l;r>l+1;r--){
long double L=dp[l][r][0]+q(l,l+1);
long double R=dp[l][r][1]+q(r,l+1);
if(L<R) dp[l+1][r][0]=L;
else{
dp[l+1][r][0]=R;
g[l+1][r][0]=1;
}
L=dp[l][r][0]+q(l,r-1);
R=dp[l][r][1]+q(r,r-1);
if(L<R) dp[l][r-1][1]=L;
else{
dp[l][r-1][1]=R;
g[l][r-1][1]=1;
}
}
}
double ans=-INF;
int s=0;
int lr=0;
for(int i=0;i<n;i++){
for(int j=0;j<=1;j++){
if(dp[i][i+1][j]<ans){
ans=dp[i][i+1][j];
s=i;
lr=j;
}
}
}
as(s,s+1,lr);
return 0;
}
代码有点问题啊,不过意会就行了,我懒得改
图论+DP
DAG上的DP与树形DP(抽象与抽象的结合)
既然与图论有关那么第一步当然是建图啦,不过这里是DP专题,所以我们跳过这部分内容,感兴趣的可以看
nature的简单图论
那我们现在来讲讲这么在图上DP,有些问题很明显我们可以记忆化搜索所以不再赘述
e,有点不知道讲什么,干脆分析几道例题吧
硬币问题:
题意:有\(n\)种硬币,面值分别为\(V1, V2······Vn\),每种都有无限多给定非负整数\(S\),可以选用多少个硬币,使得面值之和恰好为\(S\)?输出硬币数目的最小值和最大值
分析:看起来和图论集贸关系没有,但是我们是可以把这道题抽象成图的,这也是图论抽象的原因,每种面值只有一个,那么我们可以把每一个面值当作一个点,进而在图上进行转移,使用一点小巧思,把初始状态设为S,目标状态为0,这样就避免了很多问题,那么我们遍历点的时就要以0为目标统计最多与最少经过的点,那么代码就不难写了:
int dp(int S)
{
if(vis[S]) return d[S];
vis[S] = -1;
int& ans = d[S];
ans = -(1<<30);
for(int i=1;i<=n;i++){
if(S >= V[i]) ans = max(ans,dp(S-V[i])+1);
}
return ans;
}
那么DAG的DP没什么好讲的,个人觉得树形DP是重难点
树形DP
树形DP太男了蒟蒻太蒻了讲错了要指出QAQ,树形DP,顾名思义就是在树上做DP,这类问题的难点在于如何从子节点向父节点转移以及图论本身的难度
P1352 没有上司的舞会这道题就是一道"典"题,我们直接设\(f_{i,j}\)第一维状态为以\(i\)为根的最大价值,那么第二维状态就可以是\(i\)是否参加舞会,当\(j==0\)时,我们有\(f[i][0]=\sum max(f[x][0],f[x][1])\),\(x\)是\(i\)的儿子,当\(j==1\)时,\(f[i][1]=\sum f[i][0]+v_i\)那么代码还不会写嘛?= ̄ω ̄=
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
int n;
int happy[N];
int f[N];
int h[N];
int cnt;
struct Edge{
int to;
int next;
}e[N];
void add(int a,int b){
e[cnt].to=b;
e[cnt].next=h[a];
h[a]=cnt++;
}
int dp[N][2];
void dfs(int u){
dp[u][1]=happy[u];
dp[u][0]=0;
for(int i=h[u];~i;i=e[i].next){
int j=e[i].to;
dfs(e[i].to);//先去搜叶节点
dp[u][1]+=dp[j][0];
dp[u][0]+=max(dp[j][1],dp[j][0]);
}
}
int main(){
cin>>n;
memset(h,-1,sizeof h);
for(int i=1;i<=n;i++){
cin>>happy[i];
}
for(int i=1;i<=n-1;i++){
int l,k;
cin>>l>>k;
f[l]=k;
add(k,l);
}
int root=0;
for(int i=1;i<=n;i++){
if(!f[i]){
root=i;
break;
}
}
dfs(root);//电风扇从根节点开始
cout<<max(dp[root][1],dp[root][0]);
return 0;
}
相似的题有P3574 [POI2014] FAR-FarmCraft
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int t[N];
int h[N*2];
struct Edge{
int to;
int next;
}e[N];
int f[N];//以X为根的子树所有人安装的最大时间
int g[N];//从X遍历回到X的时间
int cnt;
void add(int a,int b){
e[cnt].to=b;
e[cnt].next=h[a];
h[a]=cnt++;
}
void dfs(int u,int fa){
vector<int> time;
for(int i=h[u];~i;i=e[i].next){
int j=e[i].to;
if(j!=fa){
dfs(j,u);//先搜叶节点保证f,g向上传递
time.push_back(j);
}
}
sort(time.begin(),time.end(),[](const int& a,const int& b){return f[a]-g[a]>f[b]-g[b];});
//排序,让f[]-g[]时间最长即需最先送到的房子在前
for(int i=0;i<time.size();i++){
f[u]=max(f[u],g[u]+1+f[time[i]]);//根:u的安装时间==max(f[u],{g[u]+到wait[i](下一层子节点)的时间==1}+子节点的安装时间);
g[u]+=g[time[i]]+2;//一个一个子节点遍历则每次回到u的时间加上g[wait]+1(去)+1(回)的时间
}
if(t[u]>g[u]&&u!=1){
f[u]=max(f[u],t[u]);
//特殊判断自己(u)安装时长是否可以更新
//且u!=1因为1要所有点遍历完后才可安装
}
}
int main(){
memset(h,-1,sizeof h);
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>t[i];
}
for(int i=2;i<=n;i++){
int a,b;
cin>>a>>b;
add(a,b);
add(b,a);
}
dfs(1,0);
cout<<max(f[1],g[1]+t[1]);//最后再更新根的状态
return 0;
}
再来分析下一道例题P2014 [CTSC1997] 选课,这是一道bagDP,呐前面讲了那么多背包DP那这个就不讲了叭~



 浙公网安备 33010602011771号
浙公网安备 33010602011771号