可持久化线段树2(随笔)

我们来写一下区间第k小啊：P3834 【模板】可持久化线段树 2

才学了主席树发现根本不会用啊QAQ
想到了0种办法将这个题和主席树联系啊，看看题解来梳理一下思路

先将原数组排序并且离散化：4 3 2 2 1 5 6

​ 1 2 3 4 5 6

令原数组长度为\(n\) ，对于原数组，统计\([0,i] (0<=i<=n)\)中的数，在离散数组（长度记为\(m\)）以线段树区间形式出现的次数，如图展示了\([0,0],[0,1],[0,2]\)三个版本的线段树所对应的值。需要注意的是，重复的数也要累入统计，如\([0,4]\)版本的线段树对应区间\((2,2)\)的值为\(2\)，即有两个\(2\)

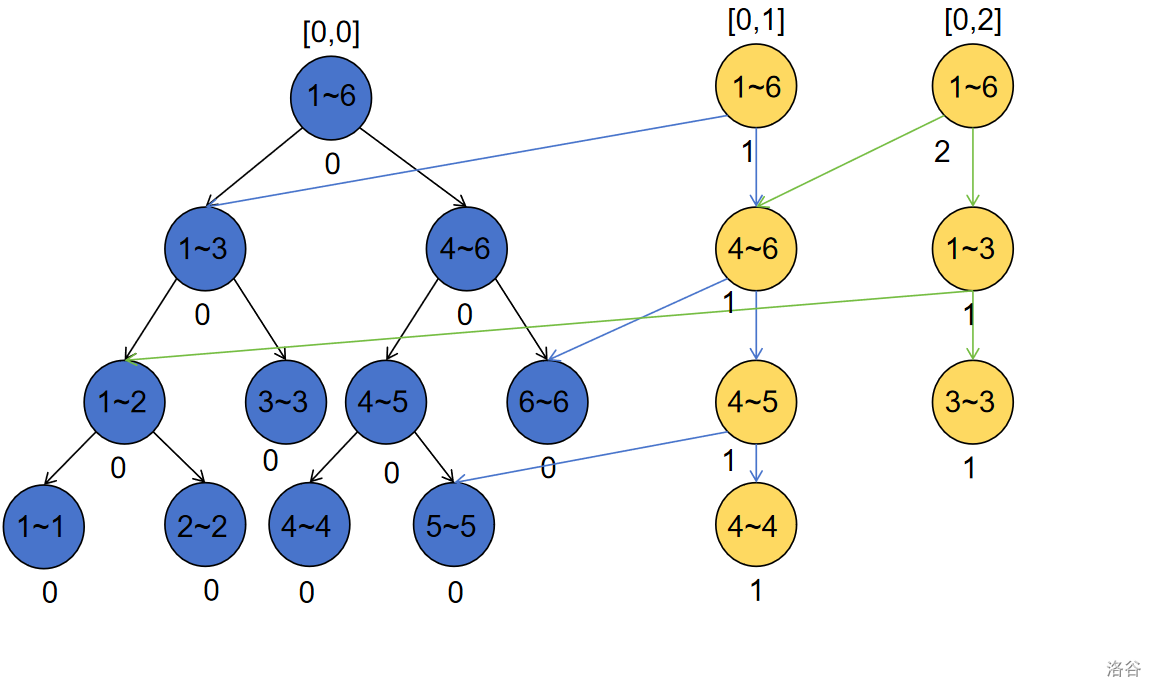
现在有两个问题：

1.怎么实现线段树版本的继承与修改？
2.这样做有什么用？

1.

我们可以先建一棵空树，空树里值全为 0 ，对应 \([0,0]\)区间 ，然后在修改操作里面将\(1-n\)的版本加入，找出这个值在离散数组中的下标，带入线段树中判断区间，包含区间加 1

2.

若询问左区间为 0，我们比较容易想到怎么去找对于\([0,i]\)的第 k 小,对于\([0,i]\)，它存储了这个区间里数的个数，而对于它的左右子树，左边所包含的数是一定比右边所包含的数小的，那么我们比较 \(k\) 与根节点左右子树的值 \(x\)，若 \(k<=x\) 那么第 \(k\) 小的数就被包含在左区间，反之为右区间，而对于包含于左区间的情况，k可以传递下去继续判断，右区间则 \(k\) 要减去左区间的 \(x\) 再继续判断，为什么呢？

（证明有点乱，理解因人而异，建议自己想为什么）

其实很好理解，\(x\) 包含于左，此时 \(k\) 值完全与右区间无关，则父节点与左子树对于 \(k\) 的询问是等价的，二者在 \(k\) 相等时的询问是包含关系。

而从属于右区间的 \(k\) 值是在累计了左区间贡献的情况下而不属于左区间的，所以此时右区间在 \(k-x\)时于父节点等价。

考虑了 \([0,i]\) 的情况，我们来考虑 \([l,r]\)的情况，其实我们只要用 \([1,r]\) 减去 \([1,l-1]\) 就行了，原因很简单，我们要找的是 \([l,r]\) 的中的数在线段树结构下出现次数，而\([1,l-1]\)与\([1,r]\)是包含的，其树形结构也完全相同，不同的只有值，所以具有可减性，由于我不想画图了所以发挥一下自己的想象力吧

代码就很简单了

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
struct SG{
	int lson;
	int rson;
	int sum;
}tr[N<<5];
int a[N];
int b[N];
int root[N<<5];
int p;
int cnt;
void build(int &u,int l,int r){
	u=++cnt;
	if(l==r){
		return ;
	}
	int mid=(l+r)>>1;
	build(tr[u].lson,l,mid);
	build(tr[u].rson,mid+1,r);
}
int add(int u){
	cnt++;
	tr[cnt]=tr[u];
	tr[cnt].sum++; 
	return cnt;
}
int modify(int u,int l,int r){
	u=add(u);//动态开点 
	if(l==r){
		return cnt;
	}
	int mid=l+r>>1;
	if(p<=mid){
		tr[u].lson=modify(tr[u].lson,l,mid);
	}
	else{
		tr[u].rson=modify(tr[u].rson,mid+1,r);
	}
	return u;
}
int query(int u,int v,int l,int r,int k){
	int ans=0;
	int mid=l+r>>1;
	int x=tr[tr[v].lson].sum-tr[tr[u].lson].sum;//线段树相减 
	if(l==r){
		return l;
	}	
	if(x>=k){
		ans=query(tr[u].lson,tr[v].lson,l,mid,k);
	}
	else{
		ans=query(tr[u].rson,tr[v].rson,mid+1,r,k-x);
	}
	return ans;
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0); 
	int n,m;
	cin>>n>>m; 
    for(int i=1;i<=n;i++){
    	cin>>a[i];
		b[i]=a[i];
	}        
    sort(b+1,b+n+1);
    int q;
    q=unique(b+1, b+n+1)-b-1;//表示去重后区间长度 
    build(root[0], 1, q);
	for(int i=1;i<=n;i++){
		p=lower_bound(b+1,b+q+1,a[i])-b;//找到当前值在离散数组中的位置 
		root[i]=modify(root[i-1],1,q);
	}
	while(m--){
		int l,r,k;
		int ans;
		cin>>l>>r>>k;
		ans=query(root[l-1],root[r],1,q,k);
		cout<<b[ans]<<endl;
	}
	return 0;
}