题解：P8047 [COCI 2015/2016 #4] GALAKSIJA

观察题意，首先删边这个操作本身就不好做，在删边的过程中，连通块也会越来越多，并不见得删边是好做的。
所以考虑正难则反，在加边的过程中统计新增的行星对。

由于加到最后是一棵树，所以不会出现加边加到同一个连通块里，即每次加边统计两个连通块之间的点是否合法即可,考虑如何去统计方案数。

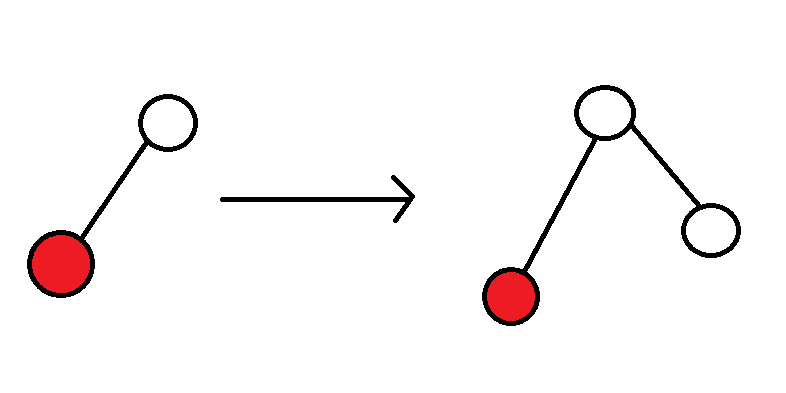
对于每个联通块，钦定一个点作为根，统计与它相连的点的距离记为数组 \(dis\)，不难发现，对于此刻与根相连的连通块，内部的点可以被递推出来。
这样做对统计方案有什么帮助吗？

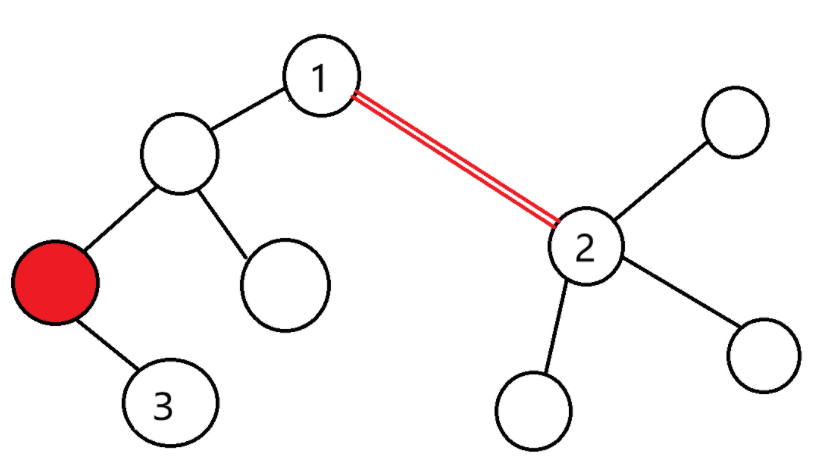
对于两个即将相连的联通块（红色边为新连的边），设红边的权值为 \(w\)。

若判断点 \(3\) 与点 \(2\) 是否合法，那么就看是否满足 \(dis_3⊕dis_1⊕w=0\) 由于我们之前预处理过，所以判断的时间复杂度是 \(O(1)\)。

稍微转换一下，我们可以求出使 \(dis_1⊕w=0\) 的值 \(x\) 并判断在集合中有哪些 \(dis\) 符合要求，这可以用 map 在 \(O(1)\) 的时间内处理整个集合，扩充到整个连通块就只需要遍历一遍。

遍历的时候遍历点更少的连通块,这样最劣情况时间为 \(O(n\log n)\) 算上 map 和并查集的时间复杂度是足以通过此题的，将求出新的 \(x\) 然后再次判断即可，在遍历集合的时候顺便统计新的 \(dis\)，将点归为同一个根，就这样处理完整个连通块，一些细节问题就见代码了。

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+10;
int h[N];
int cnt;
struct Edge{
	int to;
	int next;
	int w;
}e[N<<1];
void add(int a,int b,int w){
	e[cnt].to=b;
	e[cnt].next=h[a];
	e[cnt].w=w;
	h[a]=cnt++;
	return ;
}
struct Edge1{
	int u,v,w;
}q[N];
int w[N];
int del[N];
int ans[N];  
int n;
int dis[N];
int size[N]; 
int f[N];
unordered_map<int,int> Xor[N];
void init(){
	cin>>n;
	for(int i=1;i<=n-1;i++){
		cin>>q[i].u>>q[i].v>>q[i].w;
	}
	for(int i=1;i<=n-1;i++){
		cin>>del[i];
	}
	for(int i=1;i<=n;i++){
		Xor[i][0]++;//初始每个点为自己的根,到自己的距离为0
		dis[i]=0;
		f[i]=i;
		size[i]=1;
	}
	memset(h,-1,sizeof h);
}
int find(int a){
	if(f[a]==a) return a;
	return f[a]=find(f[a]);
}
int now;
void dfs(int u,int fa,int x)
{
	ans[now]+=Xor[find(fa)][x];//联通块内满足要求的点的数量 
	dis[u]=x;
	f[u]=f[find(fa)];
	for(int i=h[u];~i;i=e[i].next){
		int v=e[i].to;
		if(v==fa){
			continue;
		}
		dfs(v,u,x^e[i].w);
	}
}
void dfs1(int u,int fa){
	//将新的点加入
	Xor[find(u)][dis[u]]++; 
	size[find(u)]++;
	for(int i=h[u];~i;i=e[i].next){
		int v=e[i].to;
		if(v==fa){
			continue;
		}
		dfs1(v,u);
	}
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);     cout.tie(0);
	init();
	for(int i=n-1;i>=1;i--){
		now=i;
		ans[i]=ans[i+1];
		int u=q[del[i]].u;
		int v=q[del[i]].v;
		add(u,v,q[del[i]].w);
		add(v,u,q[del[i]].w);
		if(size[find(u)]>size[find(v)]){
			dfs(v,u,dis[u]^q[del[i]].w);
			dfs1(v,u); 
		}
		else{
			dfs(u,v,dis[v]^q[del[i]].w);
			dfs1(u,v); 
		}
	}
	for(int i=1;i<=n-1;i++){
		cout<<ans[i]<<endl;
	}
	cout<<"0"<<endl;
	return 0;
}