线段树学习笔记
线段树的基础知识
什么是线段树
线段树是一种分治思想的二叉树结构,用于在区间上进行信息维护与统计,与按照二进制进行区间划分的树状数组相比,线段树是一种更为通用的数据结构:
- 线段树的每一个节点都代表一个区间。
- 线段树有唯一的根节点,代表的区间是整个统计的范围。
- 线段树的每一个叶子节点都代表一个长度为 \(1\) 的元区间 \([x,x]\)。
- 定义对于每个内部节点 \([l,r]\) ,定义 \(mid = \lfloor (l + r)/2\rfloor\),它的左子节点为 \([l,mid]\),右子节点为 \([mid+1,r]\)。
除去线段树的最后一层,整棵线段树一定是一棵完全二叉树,深度为 \(O(\log N)\)。因此,可以按照与二叉堆类似的“父子二倍”节点编号方法:
- 根节点编号为 \(1\)。
- 编号为 \(x\) 的节点的左子节点编号为 \(x\times2\),右子节点编号为 \(x\times2+1\)。
在理想情况下,\(N\) 个叶节点的满二叉树有 \(2\times N-1\) 个节点。应为在上述储存方式下,最后还有一层产生了空余,所以保存线段树的数组长度不应少于 \(4\times N\)。
线段树的基本操作
线段树的建树
给定一个长度为 \(N\) 的序列 \(A\),我们可以在区间 \([1,N]\) 上建立一棵线段树,每个叶节点 \([i,i]\) 储存 \(A[i]\) 的值。以区间最大值为例,代码如下:
int a[100005];
struct node{
int l,r,date;
#define l(x) t[x].l;
#define r(x) t[x].r;
#define date(x) t[x].date;
}t[100005*4];
void build(int p,int l,int r){
l(p)=l;
r(p)=r;
if(l==r){
date(p)=a[l];
return;
}
int mid=(l+r)/2;
build(p*2,l,mid);
build(p*2+!,mid+1,r);
date(p)=max(date(p*2),date(p*2+1));
}
线段树的单点修改
将 \(A[x]\) 的值修改为 \(v\)。在线段树中,根节点是执行各种操作的入口。我们需要从根节点开始,递归找到代表区间 \([x,x]\) 的叶节点,然后从下往上更新 \([x,x]\) 以及它所有的祖先节点上保留的信息。时间复杂度为 \(O(\log n)\)。
void change(int p,int x,int v){
if(l(p)==r(p)){
date(p)=v;
return;
}
int mid=(l(p)+r(p))/2;
if(x<=mid) change(p*2,x,v);
else change(p*2+1,x,v);
date(p)=max(date(p*2),date(p*2+1));
}
线段树的区间查询
查询序列 \(A\) 在区间 \([l,r]\) 上的最大值。从根节点开始,递归执行下列过程:
- 若 \([l,r]\) 完全覆盖了当前节点代表的区间,立即回溯,并且该节点的 \(date\) 值为候选项。
- 若左子节点与 \([l,r]\) 有重叠部分,递归访问左子节点。
- 若右子节点与 \([l,r]\) 有重叠部分,递归访问右子节点。
int ask(int p,int l,int r){
if(l<=l(p) && r>=r(p)) return date(p);
int mid=(l(p)+r(p))/2,v=-(1<<30);//负无穷大
if(l<=mid) v=max(v,ask(p*2,l,r));
if(r>mid) v=max(v,ask(p*2+1,l,r));
return v;
}
线段树的区间修改
在区间修改操作中,如果某个节点被修改区间 \([l,r]\) 完全覆盖,那么以该节点为根的整棵子树都将发生变化,如果逐一进行更新,那么将使一次区间修改的时间复杂度增加至 \(O(n)\),效率不高。
假设我们逐一修改了被查询区间完全覆盖的节点 \(P\) 所代表的区间 \([l,r]\),但是在之后的查询操作中没有用到该区间的子区间作为答案,那么我们对以 \(P\) 为根的子树的修改都是没有意义的。
这启发我们在后续修改操作中,同样也可以在修改区间完全覆盖当前节点代表的区间时立即返回,但是在回溯之前在 \(P\) 上打上标记,表示“该节点曾经被修改,但它的子节点没有被更新”。
在后续的指令中,需要从节点 \(P\) 向下递归,我们再检查 \(P\) 是否被标记。如果有标记,则根据信息更新它的两个子节点并在子节点上打标记,然后清除 \(P\) 上的标记。
区间查询,区间修改的时间复杂度均为 \(O(\log n)\)。
模板
以【模板】线段树1为例
#include<bits/stdc++.h>
using namespace std;
struct node{
int l,r;
long long sum,add;
#define l(x) tree[x].l
#define r(x) tree[x].r
#define sum(x) tree[x].sum
#define add(x) tree[x].add
}tree[100005*4];
int n,m,t1,t2,t3,t4,a[100005];
void build(int p,int l,int r){
l(p)=l;
r(p)=r;
if(l==r){
sum(p)=a[l];
return;
}
int mid=(l+r)/2;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
sum(p)=sum(p*2)+sum(p*2+1);
}
void spread(int p){
if(add(p)){
sum(p*2)+=add(p)*(r(p*2)-l(p*2)+1);
sum(p*2+1)+=add(p)*(r(p*2+1)-l(p*2+1)+1);
add(p*2)+=add(p);
add(p*2+1)+=add(p);
add(p)=0;
}
}
void change(int p,int l,int r,int d){
if(l<=l(p) && r>=r(p)){
sum(p)+=(long long)d*(r(p)-l(p)+1);
add(p)+=d;
return;
}
spread(p);
int mid=(l(p)+r(p))/2;
if(l<=mid) change(p*2,l,r,d);
if(r>mid) change(p*2+1,l,r,d);
sum(p)=sum(p*2)+sum(p*2+1);
}
long long ask(int p,int l,int r){
if(l<=l(p) && r>=r(p)) return sum(p);
spread(p);
int mid=(l(p)+r(p))/2;
long long v=0;
if(l<=mid) v+=ask(p*2,l,r);
if(r>mid) v+=ask(p*2+1,l,r);
return v;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
while(m--){
cin>>t1>>t2>>t3;
if(t1==1){
cin>>t4;
change(1,t2,t3,t4);
}
else{
cout<<ask(1,t2,t3)<<endl;
}
}
return 0;
}
动态开点
普通的线段树需要开 \(4n\) 大小的数组来储存,为了节省空间,我们可以不一次性建好树,当需要用到某个节点但是该节点没有被建出时,再建出这个节点,可以用四个字来概括动态开点的核心思想——要用再建。
代码如下:
#include<bits/stdc++.h>
using namespace std;
struct node{
int son_l,son_r;
long long sum,tag;
#define son_l(x) t[x].son_l
#define son_r(x) t[x].son_r
#define sum(x) t[x].sum
#define tag(x) t[x].tag
}t[100005*2];
int tot=1,root=1,n,m;
void add(int &p,int l,int r,long long d){
if(!p) p=++tot;
sum(p)+=(r-l+1)*d;
tag(p)+=d;
}
void spread(int p,int l,int r){
if(l>=r) return;
int mid=(l+r)>>1;
add(son_l(p),l,mid,tag(p));
add(son_r(p),mid+1,r,tag(p));
tag(p)=0;
}
void change(int p,int l_now,int r_now,int l_to,int r_to,int d){
if(l_to<=l_now && r_to>=r_now){
add(p,l_now,r_now,d);
return;
}
spread(p,l_now,r_now);
int mid=(l_now+r_now)>>1;
if(l_to<=mid) change(son_l(p),l_now,mid,l_to,r_to,d);
if(r_to>mid) change(son_r(p),mid+1,r_now,l_to,r_to,d);
sum(p)=sum(son_l(p))+sum(son_r(p));
}
long long ask(int p,int l_now,int r_now,int l_to,int r_to){
if(l_to<=l_now && r_to>=r_now){
return sum(p);
}
spread(p,l_now,r_now);
int mid=(l_now+r_now)>>1;
long long val=0;
if(l_to<=mid) val+=ask(son_l(p),l_now,mid,l_to,r_to);
if(r_to>mid) val+=ask(son_r(p),mid+1,r_now,l_to,r_to);
return val;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
int t;
cin>>t;
change(root,1,n,i,i,t);
}
while(m--){
int t1,t2,t3,t4;
cin>>t1>>t2>>t3;
if(t1==1){
cin>>t4;
change(root,1,n,t2,t3,t4);
}
else{
cout<<ask(root,1,n,t2,t3)<<endl;
}
}
return 0;
}
可持久化线段树
以上,我们讨论的线段树都只能解决对当前数据进行操作的问题,如果想解决对任意时间下的数据进行操作的问题,我们就需要对线段树进行可持久化的改造。
以线段树的单点修改,区间查询最大值为例,单点修改操作只会使 \(O(n \log n)\) 个节需要修改,我们可以对这些节点 \(p\) 分别创建一个副本 \(p'\),若 \(p\) 不是线段树的叶子节点,则 \(p\) 的左子树或右子树必然被更新,以被更新的是左子树 \(l\) 为例,我们在 \(l\) 中递归,在返回时将 \(p'\) 的左子树改为 \(l'\),右子树仍与 \(p\) 的右子树相同,然后更新 \(p'\) 上保存的区间最大值即可。
需要注意的是,经过这样改造的线段树将不再是一颗完全二叉树,所以我们不能沿用父子二倍编号法。
模板题。
代码如下:
#include<bits/stdc++.h>
using namespace std;
inline int read(){register int t1=0,t2=0;register char x=getchar();while(x<'0' ||x>'9'){if(x=='-') t2|=1;x=getchar();}while(x>='0' && x<='9'){t1=(t1<<1)+(t1<<3)+(x^48),x=getchar();}return t2?-t1:t1;}
inline void write(int x){register int sta[35],top=0;if(x<0) putchar('-'),x=-x;do{sta[top++]=x%10,x/=10;}while(x);while(top) putchar(sta[--top]+48);}
int n,m,a[1000005],root[1000005],tot;
struct node{
int l,r,data;
}t[1000005<<5];
int build(int l,int r){
int p=++tot;
if(l==r){
t[p].data=a[l];
return p;
}
int mid=l+r>>1;
t[p].l=build(l,mid);
t[p].r=build(mid+1,r);
return p;
}
inline int change(int now,int l,int r,int x,int val){
int p=++tot;
t[p]=t[now];
if(l==r){
t[p].data=val;
return p;
}
int mid=l+r>>1;
if(x<=mid) t[p].l=change(t[now].l,l,mid,x,val);
else t[p].r=change(t[now].r,mid+1,r,x,val);
return p;
}
inline int ask(int now,int l,int r,int x){
if(l==r) return t[now].data;
int mid=l+r>>1;
if(x<=mid) return ask(t[now].l,l,mid,x);
else return ask(t[now].r,mid+1,r,x);
}
int main(){
n=read();
m=read();
for(int i=1;i<=n;i++){
a[i]=read();
}
root[0]=build(1,n);
for(int i=1;i<=m;i++){
int t1=read(),t2=read(),t3=read();
if(t2==1){
int t4=read();
root[i]=change(root[t1],1,n,t3,t4);
}
else{
write(ask(root[t1],1,n,t3));
putchar('\n');
root[i]=root[t1];
}
}
return 0;
}
一些例题
The Child and Sequence
题目链接。
解法分析
设模数为 \(mod\),当修改区间 \([l,r]\) 中的最大值小于 \(mod\) 时不应该继续尝试修改。这启示我们在遇到这类在区间上做运算的问题时,应挖掘该运算的特殊性质,减少不必要的递归和修改。
Code
#include<bits/stdc++.h>
using namespace std;
int n,m,a[100005];
struct node{
int l,r;
long long sum,mx;
#define l(x) t[x].l
#define r(x) t[x].r
#define sum(x) t[x].sum
#define mx(x) t[x].mx
}t[100005*4];
void build(int p,int l,int r){
l(p)=l;
r(p)=r;
if(l==r){
sum(p)=a[l];
mx(p)=a[l];
return;
}
int mid=(l+r)/2;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
sum(p)=sum(p*2)+sum(p*2+1);
mx(p)=max(mx(p*2),mx(p*2+1));
}
void change(int p,int x,long long v){
if(l(p)==r(p)){
sum(p)=v;
mx(p)=v;
return;
}
int mid=(l(p)+r(p))/2;
if(x<=mid) change(p*2,x,v);
else change(p*2+1,x,v);
mx(p)=max(mx(p*2),mx(p*2+1));
sum(p)=sum(p*2+1)+sum(p*2);
}
void change_mod(int p,int l,int r,long long d){
if(l<=l(p) && r>=r(p) && mx(p)<d) return;
if(l<=l(p) && r>=r(p) && l(p)==r(p)){
mx(p)%=d;
sum(p)%=d;
return;
}
int mid=(l(p)+r(p))/2;
if(l<=mid) change_mod(p*2,l,r,d);
if(r>mid) change_mod(p*2+1,l,r,d);
sum(p)=sum(p*2)+sum(p*2+1);
mx(p)=max(mx(p*2),mx(p*2+1));
}
long long ask(int p,int l,int r){
if(l<=l(p) && r>=r(p)) return sum(p);
int mid=(l(p)+r(p))/2;
long long v=0;
if(l<=mid) v+=ask(p*2,l,r);
if(r>mid) v+=ask(p*2+1,l,r);
return v;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
build(1,1,n);
while(m--){
int t1;
cin>>t1;
if(t1==1){
int t2,t3;
cin>>t2>>t3;
cout<<ask(1,t2,t3)<<endl;
}
else if(t1==2){
int t2,t3,t4;
cin>>t2>>t3>>t4;
change_mod(1,t2,t3,t4);
}
else if(t1==3){
int t2,t3;
cin>>t2>>t3;
change(1,t2,t3);
}
}
return 0;
}
Legacy
题目链接。
相关知识:线段树优化建图
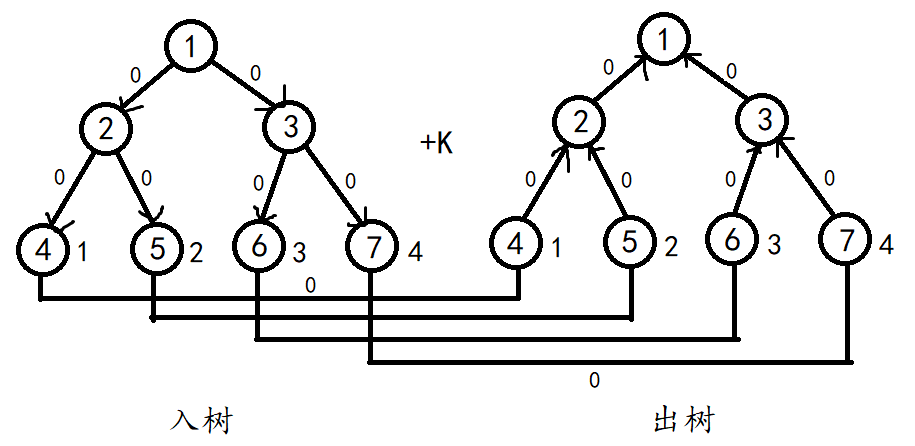
注:图片来自@123wwm。
建立两棵线段树,一棵为“入树”,一棵为“出树”,树中的叶子节点即为图中的节点。
在图中代表相同的节点的出树与入树上的点需要连接一条权值为 \(0\) 的无向边。在入树中,父节点与该节点的两个子节点之间需要从父节点分别向它的两个子节点连一条的权值为 \(0\) 的有向边。在出树中,父节点与该节点的两个子节点之间需要从两个子节点分别向它们的父节点连一条的权值为 \(0\) 的有向边。
在进行区间向点连边或点向区间连边的操作时,在代表这一区间的出树上的节点与需要连边的在入树上的叶子节点之间连一条有向边。
解法分析
使用线段树优化建图之后,跑一遍 dijkstra 算法求最短路即可。
Code
#include<bits/stdc++.h>
using namespace std;
int n,Q,s,a[100005],k;
long long dis[1000005];
struct tree{
int l,r;
#define l(x) t[x].l
#define r(x) t[x].r
}t[100005*4];
struct node{
int to;
long long l;
};
vector<node> v[1000005];
struct node1{
int now;
long long sum;
};
bool operator <(const node1 &x,const node1 &y){
return x.sum>y.sum;
}
priority_queue<node1> q;
bool vis[1000005];
void build(int p,int l,int r){
l(p)=l;
r(p)=r;
if(l==r){
a[l]=p;
return;
}
v[p].push_back((node){p<<1,0});
v[p].push_back((node){p<<1|1,0});
v[(p<<1)+k].push_back((node){p+k,0});
v[(p<<1|1)+k].push_back((node){p+k,0});
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
}
void change(int p,int l,int r,int to,int lo,int m){
if(l<=l(p) && r>=r(p)){
if(m==3) v[p+k].push_back((node){to,lo});
else v[to+k].push_back((node){p,lo});
return;
}
int mid=(l(p)+r(p))>>1;
if(l<=mid) change(p<<1,l,r,to,lo,m);
if(r>mid) change(p<<1|1,l,r,to,lo,m);
}
void dijkstra(){
memset(dis,0x3f,sizeof(dis));
dis[a[s]+k]=0;
q.push((node1){a[s]+k,0});
while(!q.empty()){
node1 x=q.top();
q.pop();
if(vis[x.now]) continue;
vis[x.now]=1;
for(int i=0;i<v[x.now].size();i++){
node net=v[x.now][i];
if(dis[net.to]>dis[x.now]+net.l){
dis[net.to]=dis[x.now]+net.l;
q.push((node1){net.to,dis[net.to]});
}
}
}
}
int main(){
cin>>n>>Q>>s;
k=5e5;
build(1,1,n);
for(int i=1;i<=n;i++){
v[a[i]].push_back((node){a[i]+k,0});
v[a[i]+k].push_back((node){a[i],0});
}
while(Q--){
int t1,t2,t3,t4,t5;
cin>>t1>>t2>>t3>>t4;
if(t1==1) v[a[t2]+k].push_back((node){a[t3],t4});
else{
cin>>t5;
change(1,t3,t4,a[t2],t5,t1);
}
}
dijkstra();
for(int i=1;i<=n;i++){
if(dis[a[i]]==0x3f3f3f3f3f3f3f3fll) cout<<-1<<" ";
else cout<<dis[a[i]]<<" ";
}
return 0;
}

 记录了线段树的基本知识以及一些例题,适合初学线段树的同学看awa。
记录了线段树的基本知识以及一些例题,适合初学线段树的同学看awa。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号