斜率优化

先言

\(ll\) ： “有空给你们讲讲 。 ”
\(nj\) ：“自己整理下学的。 ”

---

闲话不多说，只先谈一下斜率优化。
个人对于斜率优化浅显的理解就是以 \(DP\) 方程为基础，建立坐标系，同时通过以 \(DP\) 方程建立的函数，通过斜率以其单调性对这个状态进行精简，从而达到优化的目的

我们知道如果状态转移类似于这般 \(f_{j} = f_{i} + lots_j\) 状态转移方程，我们可以用单调队列进行优化，从而将 \(O(n^2)\) 的复杂度成功下调至 \(O(n)\) 的，优化幅度是很大的。但是如果 \(f_{j} = f_{i} + a_i \times b_j + c_i + d_j\) 很显然，由于 \(a_i \times b_j\) 的存在，我们是无法将 \(i,j\) 进行分离，也就是，我们无法用单调队列优化。但是这种我们是可以用斜率优化进行优化的 。

引入

状态转移方程

我不打算直接引入题目，我引入一个状态转移方程，我们来对其进行优化。

\[f_i = min( f_j + M + (sum_i - sum_j ) ^ 2 ) \]

显然，我们将其化开，我们是得不到能用单调队列优化的影子的。 我们不妨设 \(j,k\) 两个决策点，我们假设 \(j\) 决策要比 \(k\) 决策优一些，我们就有

\[\therefore f_j + M + (sum_i - sum_j)^2 < f_k + M + (sum_i - sum_k)^2 \]

继续推导

我们直接将其化开

\[\therefore f_j + M + sum_i ^2 - 2\times sum_i \times sum_j + sum_j^2 < f_k + M + sum_i^2- 2\times sum_i \times sum_k + sum_k^2 \]

合并一下同类项

\[f_j + sum_j^2 - 2\times sum_i \times sum_j <f_k + sum_k^2 - 2\times sum_i \times sum_k \]

我们选择进行一下化简

\[f_j + sum_j^2 - (f_k + sum_k ^ 2) < 2 \times sum_i \times (sum_j - sum_k) \]

如果 $j > k $

\[\frac{f_j + sum_j^2 - (f_k + sum_k^2)}{(sum_j - sum_k)} < 2\times sum_i \]

如果 $j < k $

\[\frac{f_j + sum_j^2 - (f_k + sum_k^2)}{ (sum_j - sum_k)} < 2\times sum_i \]

那么我们将 \(f_i + sum_i\) 看成 \(f(x)\) ,将 \(2\times i\) 看成 \(x\) ,那这个式子的左边也就发现 \(\frac{f(j) - f(k)}{j - k}\) , 那么我们就显然的可以看成，这个式子表示的是斜率呀。

那也就等价于

• \(j < k\) 并且 \(\frac{f(j) - f(k)}{j - k} < 2\times sum_i\) , 说明决策 \(j\) 更优一些 。
• \(j > k\) 并且 \(\frac{f(j) - f(k)}{j - k} <2\times sum_i\) ， 说明决策 \(j\) 更优一些 。

感性理解就是，如果两个决策点的斜率小于 \(sum_i\) 那么就是靠后的决策点更优，否则就是靠前的更优。

---

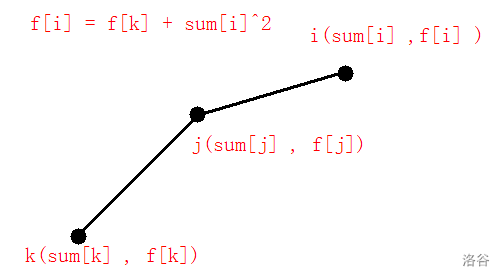
假设几个量 ：

• \(f_i\) 就是我们表示函数 \(f(i)\)
• \(sum_i\) (有时候可能手一抖写成 \(num_i\) ，还望见谅) 表示我们说的 \(x\)
• \(t\) 表示我们当前这个点 (也就是要求求解的点)
• \(i,j,k\) 表示 \(t\) 这个点转移的时候，可以从 \(i,j,k\) 这三个点进行转移 。

很显然我们是可以看得出， \(k < j < i\) 。
那么 他们与 \(s\times sum_t\) 有三种关系

• \[\frac{f_j - f_k}{sum_j - sum_k} > \frac{f_i - f_j}{sum_i - sum_j} > 2\times sum_t \]

显然，此时 \(k\) 比 \(j\) 优 ， \(j\) 比 \(i\) 优 。

• \[\frac{f_j - f_k}{sum_j - sum_k} > 2\times sum_t > \frac{f_i - f_j}{sum_i - sum_j} \]

显然，此时 \(k\) 比 \(j\) 优， \(i\) 比 \(j\) 优

同时

\[2\times sum_t > \frac{f_j - f_k}{sum_j - sum_k} > \frac{f_i - f_j}{sum_i - sum_j} \]

显然 \(j\) 比 \(k\) 优， \(i\) 比 \(j\) 优。

所以，当这个 \(\vec{ji}\) 的斜率 > $ \vec{jk}$ 的斜率 ，并且 \(k < j < i\) , 这个时候， \(j\) 是不做状态转移的，也就是说，我们可以将 \(j\) 从决策集合中删除 。

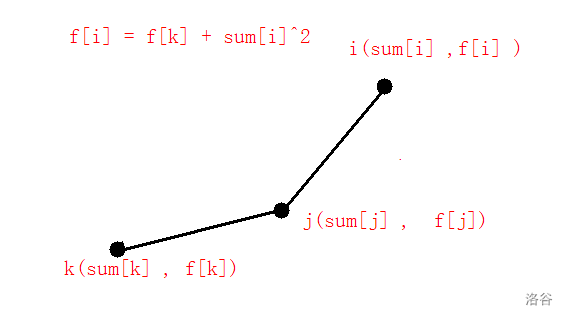
如果进行决策点是这样的，也就是一个下凸的，那么决策 \(j\) 是最优的。

可以得知 ， 决策之间，斜率是递增，我们可以二分 。

所以我们二分斜率比 \(2\times sum_t\) 小的编号最大的点就是最优决策 。

如果不是递增的怎么办 ？
也是可以做的，但是难且麻烦，需要用到 \(CDQ\) 分治，或用平衡树维护凸包，笔者不会。

最后我们单调队列维护凸包，从单调队列中弹出那些不可能再合法的元素

例题1 P3195 [HNOI2008]玩具装箱

【description】 :

见题面

【solution】:

相信大家是能够推出状态转移方程的。这里状态转移就直接说了

\[f_i = \min(f_j + (\sum_{k=j + 1}^{i} c_k + i - j - l - 1)^2) \]

对于 \(\sum_{k=j+1}^{i} c_k\) 我们是可以用 \(sum\) 数组进行一下预处理的，其实我们就得到了

\[f_i = \min(f_j + (sum_i - sum_j + i - j - l - 1) ^2) \]

我们将 \(sum_i + i\) 看做一个整体 \(t\) 那么我们同样可以化简得到式子

\[f_i = \min(f_J + (t_i - t_j - 1 - L) ^2) \]

这样我们去直接展开这个式子要简单的多了。

我们仿照上面的例子，我们假设 \(j\) 这个决策点比 \(k(j< k)\) 更优一些。我们就可以得到
\(f_j + (t_i - t_j - 1 - L)^2 < f_k + (t_i - t_k - L - 1) ^ 2\)
继续化简我们就得到 .

\[f_j + t_i^2 - 2\times t_i \times (t_j + 1 + L )^2 + (t_j + L + 1) ^ 2 < f_k + t_i ^2 - 2\times t_i \times(t_k + 1 + L) ^2 + (t_k + 1 +L )^2 \]

\(continue\) 化简 得到

\[2\times t_i \times(t_k + 1 + L) - 2\times t_i \times(t_j + 1 + L) \geq f_k + (t_k + 1 + L) ^2 - (f_j +(t_j + 1 +L) ^2 ) \]

所以我们就得到了，由于 $ (t_i + 1 + L )^2$ 写起来实在是麻烦，我们用 \(G_i\) 来表示
\(2\times t_i \geq \frac{f_k + G_k - (f_j + G_j)}{t_k - t_j}\)

结合上面的证明，我们同时可以知道斜率是递增的。然后就 \(OK\) 了。

【Code】

例题2 P5785 [SDOI2012]任务安排

【description】 :

见题面

【solution】:

这个状态是十分好设计的。 我们设 \(f_i\) 表示以 \(i\) 为结束任务的最小的费用。那么我们就有状态转移

\[f_i = \min (f_j + S\times \sum_{k = j + 1}^{n}c_k + T_i\times\sum_{k = j+1}^{i} c_k) \]

来解释一下该状态转移方程 。

\(S\times\sum_{k=j+1}^{n}c_k\) 表示的是开机一次 \(S\) 的给出的贡献。
\(T_i \times \sum_{k=j+1}^{i}c_k\) 表示完成任务 \(k\) 的贡献。

我们定义以下变量 ：

• \(sumc\) 表示钱数的前缀和
• \(sumt\) 表示时间的前缀和

\[f_i = \min(f_j + s \times (sumc_n - sumc_j ) + sumt_i \times (sumc_i - sumc_j) ) \]

预计复杂度 \(O(n^2)\) ，很显然，这道题是过不了的，我们考虑直接展开，便于寻找性质

\[f_i = \min(f_j + s\times sumc_n - s\times sumc_j + sumt_i\times sumc_i - sumc_i \times sumc_j) \]

我们发现，这个状态转移出现了 \(sumt_i \times sumc_j\) 这个乘积的形式，我们考虑一下是否能进行斜率优化。我们设 \(j,k(j < k)\) 两个决策点，同时决策点 \(j\) 比决策点 \(k\) 要更优以一些，我们就有

\[f_j+ s\times sumc_n - s\times sumc_j + sumt_i \times sumc_i - sumt_i \times sumc_j <= f_k + s\times sumc_n - s\times sumc_k + sumt_i \times sumc_i - sumt_i \times sumc_k \]

我们继续化简

\[f_j - s\times sumc_j - sumt_i \times sumc_j \leq f_k - s\times sumc_k - sumt_i \times sumc_k \]

移项

\[(f_j - s\times sumc_j ) - (f_k - s\times sumc_k) \leq sumt_i \times (sumc_j - sumc_k) \]

然后我们就因为 \(j < k , \therefore sumc_j < sumc_k\)

\[\frac{ (f_j - s\times sumc_j ) - (f_k - s\times sumc_k) }{sumc_j - sumc_k}\geq sumt_i \]

然后我们就发现，可完全可以进行斜率优化了。又 \(\because |t_i| \leq 2^8\) 所以，不满足单调性了，也就是说，我们不能够用单调队列优化DP了，但是我们还是可以用单调队列储存一下决策点，同时我们直接二分找到我们的所需要转移的决策点。

【Code】

【CF311B Cats Transport】

【descriprion】:

见题面

【solution】:

对于每一只猫，如果想要接走他，我们发现，就是从 \(T_i - \sum_{j=1}^{H_i} d_j\) 的时刻出发，才能接到它，同时这个时候猫是不需要等待的。

以下是一些变量的解释 ：

• \(cat_i\) 表示的是接上第 \(i\) 只猫，我们需要从 \(cat_i\) 的时刻出发
• \(f_{i,j}\) 表示的前 \(i\) 个饲养员带走了 \(j\) 只猫，猫的最小等待和。

我们预处理出 \(cat\) 数组，根据贪心策略，我们可以知道铲屎官带走的猫必然是带走的是一段连续的区间的猫

我就是一开始并不知道这个结论，我 \(TM\) 就是打不出来状态转移
首先我们说明一下 \(cat\) 数组的意义，我们让 \(T_i - \sum_{k=1}^{i}d_i\) 我们让这只猫玩耍的结束时间减去到达该点路程(根据这个速度，我们知道这样也算是时间)，我们将相当于直接把这只猫平移到 \(1\) 号山丘上了，那么我们如果在 \(a_j\) 去接的话 , \(j\) 前面的必然已经玩耍完了(这里的 \(j\) 是根据 \(cat\) 数组排序得到的顺序) ，那么让猫多等一会必然会比猫少等一会更差，所以我们选择接上猫，显然答案会更优，所以，也就是说，接上的必然是一段连续区间的猫。

假设第 \(i\) 个铲屎官带走了 \(k + 1\to j\) 只猫，那么饲养员最早出发的时间就是 \(cat_j\) ，其他的猫，等待时间之和就是 \(\sum_{i=k}^{j} cat_j - cat_i\) ，也就是下边：

\[f_{i,j} = \min(f_{i-1,k} + cat_j \times (j-k) - (\sum_{l=1}^{j}cat_l - \sum_{l=1}^{k}cat_l)) \]

首先我们是可以用一个前缀和将两个 \(\sum\) 给优化掉的，那么我们式子就变成了。

\[f_{i,j} = \min(f_{i-1,k} + cat_j + cat_j \times (j-k) - (sum_j - sum_k)) \]

所以我们就得到一个 \(O(m^2p)\)的做法，很显然这样是过不了的。我们考虑能否将状态转移转成 \(O(1)\) 的。

我们发现决策 \(k\) 与当前 \(cat_j\) 相乘，那么我们就容易想到斜率优化搞一下。

我们先将 \(\min\) 删去，保留 \(k\) ，搞一下
我们就得到

\[f_{i,j} = f_{i-1,k} + cat_j \times j - cat_j \times k - sum_j + sum_k \]

然后就有

\[f_{i,j} = f_{i-1,k} + cat_j \times j - sum_j - (cat_j \times k - sum_k) \]

\[f_{i,j} + cat_j \times k - cat_j \times j + sum_j= f_{i-1,k} + sum_k \]

\[\frac{(f_{i,j} + sum_j)- (f_{i-1,k} + sum_k) }{j-k} = cat_j \]

我们以 \(k\) 这个决策作为自变量，将 \(f_{i-1,k} + sum_k\) 作为因变量，同样的，我们也是完全可以明白 \(cat_j\) 是作为斜率的吧。(不一定像上方一样，非要两个决策，这样也是可以的，毕竟这个式子不复杂，也就是不需要删去同类项，并且自带决策点)

使得截距最小，那就是维护一个下凸包。用单调队列维护即可。

因为我们已经将 \(cat\) 数组排好序了，也就是说，我们保证 \(cat\) 是单调递增的了，也就是斜率是单调递增的了，所以单调队列优化即可。

【Code】

小结

如果以后能碰上更有趣的斜率优化题目的话，会重新填坑，或者如果有机会学 \(CDQ\) 分治或者平衡树维护凸包的话，也会回来填坑的。毕竟笔者实在太菜 。

整体来说，斜率优化是比较套路化的，在推出状态转移方程的时候，我们得到决策点 \(k\) 与一个不知名的但是一个随着 \(i\) 变化而变化的量的时候，我们就选择用斜率优化进行优化，基本的模型已经在前面说了，这里还是再次赘述一下 \(f_{i} = \min(f_{j} + k_i \times a_i + c_i + d_j )\)

但是从上面做的三道题来说，最后一题，我反而认为状态转移是一个难点，我当时是没能够推导出来的。

题单

例题就不再赘述了

P4360 [CEOI2004]锯木厂选址
P3628 [APIO2010]特别行动队
P2120 [ZJOI2007]仓库建设
#10191. 「一本通 5.6 练习 4」打印文章
其他的题目后续加，这些都是类似于模板题的题目

鸣谢

玩具装箱题解
[算法]斜率优化
动态规划（DP）优化之斜率优化讲

告一段落了。