单调队列
1. 【板子】单调队列
【题目描述】：
有一个长为\(n\)的序列\(a\)，以及一个大小为\(k\)的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。
【分析】：
根据题意，我们分析可以得出，题目的要求也就是在一个长度为\(k\)的序列中维护一个最大值和最小值，只不过这个序列是动态的罢了。所以我们先画一个图，（感谢洛谷友情赞助）
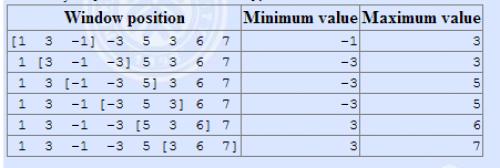,都快省下我说了，就来分析一下这个样例就好了
只分析，最大值，最小值类比即可（就是换个小于号的事）首先 我们先设出\(q\)这么一个序列，这个序列我们让他成为单调递增的（肯定先置零）首先会直接搞成\(1,3\)（因为是递增的，-1被略过去了），再去向后找，找到了\(-3\)，这个时候发现，区间里的最大值\(3\)比这个数大，略过这个数，向后找，找到了\(5\)，这时候序列只有两个数值，也就是\(1,3\),现在在加上5，形成了\(1,3,5\)，继续向后寻找，找到了\(6\)，又比最大值要大，我呢边想让他入这个序列，这个序列长度最大就是\(3\),所以，\(1\)就骂骂咧咧地退出了序列。继续向后寻找，找到了\(7\),同上，\(3\)骂骂咧咧地离开了序列，再进行寻找，没有了，然后就结束了，最后的序列成了\(5,6,7\)恰好也就是单调上升的，这不过这个题，每一次滑动都输出一下，序列第一个数就\(OK\)了。我的代码\(q\)存的是下标
【\(code\)】:
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <iostream>
#include <queue>
using namespace std;
const int maxn=1e6+120;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n,k;
int a[maxn];
int q[maxn];
void min_queue()
{
int head1=1,tail1=0;
for(int i=1;i<=n;i++)
{
while(a[q[tail1]]>=a[i]&& tail1>=head1)
{
tail1--;
}
q[++tail1]=i;
if(q[tail1]-q[head1]+1>k) head1++;
if(i>=k)
{
printf("%d ",a[q[head1]]);
}
}
}
void max_queue()
{
memset(q,0,sizeof(q));
int head2=1,tail2=0;
for(int i=1;i<=n;i++)
{
while(a[q[tail2]]<=a[i] &&tail2>=head2)
{
tail2--;
}
q[++tail2]=i;
if(q[tail2]-q[head2]+1>k) head2++;
if(i>=k)
{
printf("%d ",a[q[head2]]);
}
}
}
int main()
{
n=read(),k=read();
for(int i=1;i<=n;i++)
{
a[i]=read();
}
min_queue();
printf("\n");
max_queue();
return 0;
}
2.单调队列优化\(DP\)
题目
由于\(lhy\)同学提的建议，所以我选择去看了一下这道题，并学习单调队列；
首先这道题的状态转移还是很好推的，直接写上吧
【状态设计】：
\(f_{i,j}\)表示在\(j\)这个区域观看地\(i\)的烟花的最大\(happiness\)
【状态转移】：
\(f_{i,j}= \max \limits_{0<k \leq d} f_{i-1,j-k}+b_i - |a_i-j|\)
此时发现，对于\(b_i\)这个参数，我们好像可以提出来，毕竟就是个参数，我们对式子进行整改
设$$f_{i,j}=min_{i=1}^n f_{i-1,j-k}-|a_i-j|$$
那么 我们设 \(sum = \sum b_i\), \(QwQ=f_{m,n}\), 我们的\(ans = sum -QwQ\)了呀，这就比较显然了，
【解题】：
我们神奇的发现，我们设的是 $f_{i,j} $ 其中 \(i\in (0,300),j\in (0,150000)\),意味着我们即将要开 \(f_{300,150000}\)的数组，开不下怎么办？我们发现，对于\(DP\)嘛，这个状态和上一个状态有一定的关联，并且，这是个线性\(DP\)，\(So\)我们可以用滚动数组直接压掉第一维，因为只与它上一个状态有关。这样，空间就解决了
更神奇的是，时间木法保证了，炸时间了 \(TLE,TLE,TLE\),但是还能得点分，我考试抱铃。现在就考虑如何解决时间问题；
我们又一次神奇的发现（这么多神奇，我\(TM\)直接找小智去抓精灵了），我们的这一次的状态\(f_{i,j}\)，其中\(i\)就不能动了，再说，已经压缩到了\(2\)了,也动不了了，考虑一下怎么搞掉后面的\(j\),我们设上一次的状态是\(f_{i-1,k}\),那么我们这一次 \(f_{i,j}\)更新中，\(j\)就一定是属于 \((k,k+d)\)的，也就说，类似于上方的单调队列模板，每一次更新的时候我们都会取一个长度\(d\)的一个滑动窗口，寻找最小值，其中我们发现有的被寻找了很多次，还有的根本不可能用来更新答案，结果我们都去进行了枚举，这无疑是让本就很慢的程序更是雪上加霜。所以我们选择用单调队列来更新，省去那些其他的不需要的枚举。
【注】：
1.本人曾在\(q_{++head}\)和\(q_{head++}\)上死了3遍，直接样例死不过
2.网站炸了5次，\(Waiting\)
3.更新的时候取最小值不会取值，我都忘了我对头维护的是最小值，WA两次,\(QwQ\)
4.没有从大到小在更新一遍，WA了3次,
5.
没有了
【code】:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#define int long long
using namespace std;
const int maxn=150000+100;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){ if(ch == '-') f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0'; ch=getchar();}
return x*f;
}
int b[maxn],a[maxn],t[maxn],f[2][maxn];
int q[maxn];
int m,n,d,sum=0,ans=0x3f3f3f3f;
signed main()
{
n=read(),m=read(),d=read();
for(int i=1;i<=m;i++)
{
a[i]=read(),b[i]=read(),t[i]=read();
sum+=b[i];
}
for(int i=1;i<=n;i++) // 进行初始化
{
f[1][i] = abs(a[1]-i);
}
for(int i=2;i<=m;i++) // 枚举每一个烟花
{
int len = (t[i] -t[i-1])*d; //如果能够在这个时间内，移动len个单位，才能要，否则看不了烟花
int head = 1;
int tail = 0;
for(int j=1;j<=n;j++)
{
while(head<=tail && q[head]<j-len) ++head;
while(head<=tail && f[(i-1)&1][q[tail]]>f[(i-1)&1][j]) --tail; // 如果上一个的以tail结尾的地方不如j结尾的地方更优，那就没有存
//在的意义了，让其出对
q[++tail] = j;
f[i&1][j]= f[(i-1)&1][q[head]] +abs(j-a[i]); //取出最小值进行更新
if(i==m)
{
ans=min(ans,f[i&1][j]);
}
}
head=1,tail=0;
for(int j=n;j>=1;j--)//分别从左和从右进行一遍更新
{
while(head<=tail&&q[head]-len>j)++head;
while(head<=tail&&f[(i-1)&1][q[tail]]>f[(i-1)&1][j])--tail;
q[++tail]=j;
f[i&1][j]=min(f[i&1][j],f[(i-1)&1][q[head]]+abs(j-a[i]));
if(i==m)
{
ans=min(ans,f[i&1][j]);
}
}
}
cout<<sum-ans<<endl;
return 0;
}
3.单调队列优化多重背包，
至于为什么单独拿出来，并不是因为它有多难，而是一它很典型，二则是我前面有一篇文章，所以需要用到这一个；
【题目】：
有\(N\)种物品和一个容量是\(V\)的背包。第\(i\)种物品最多有\(s_i\)件，每件体积是\(v_i\)，价值是\(w_i\)。求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。输出最大价值。
【题目分析】：
按照常理我们仍然是讲其中的多个背包拆分拆成\(01\)背包来处理；
在进行单调队列优化的时候，我们需要上一层状态来对这一次的状态进行一个筛选，所以我们也就需要重新来一个数组，来记录上一个状态；设为\(pre\)数组，同时我们要求的是价值最大，那么单调队列\(q\)也就要维护最大值，这里维护的是下标，例如上面的题目就是下标，对于头和尾的处理稍微说一下吧，（凑个字数）
对于\(head\),其中这个是\(q_{head}\)维护的是这个区间的最大值的下标，但是如果我们超出了长度也就是总数\(s_i\)的限制，就需要弹出
对于\(tail\),如果这个的价值要小于上一层的价值，那么这个价值也不要了，弹出；
\(OK\)
【code】:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
using namespace std;
const int maxn=1e6;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){ if(ch == '-') f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0'; ch=getchar();}
return x*f;
}
int N,V;
int f[maxn],q[maxn],pre[maxn];
int main()
{
N=read(),V=read();
for(int i = 1;i <=N;i++)
{
memcpy(pre,f,sizeof(f));//存储上一层的状态
int w=read(),v=read(),s=read();
for(int j=0;j<v;j++) //背包枚举体积
{
int head=1,tail=0;
for(int k = j;k<=V;k+=v) //枚举可以加的体积
{
//q维护的是最大值的编号
while(head<=tail&&k-s*v>q[head]) head++;
while(head<=tail&&pre[q[tail]]+(k-q[tail])/v * w<=pre[k]) tail--;
q[++tail] =k;
f[k]=pre[q[head]] + (k-q[head])/v * w;
}
}
}
printf("%d",f[V]);
return 0;
}
4.【题目】围栏
【状态设计】：
\(f_{i,j}\)表示前\(i\)个工匠，粉刷了第\(j\)块木板的最大价值
【状态转移】：
1.很显然，有两个转移方程，分别对应着第\(i\)个工匠不刷，或者第\(j\)块木板不刷；
第\(i\)工匠不刷 $f_{i,j} =f_{i-1,j} \(
第\)j\(块木板不刷 ，\)f_{i,j}=f_{i,j-1}$
接下来就是刷的情况了，先列出状态转移方程，
首先，状态肯定是又上一个工匠转移而来，类比\(01\)背包，我想把第一维滚掉，没成功，然后继续看状态转移方程吧，状态之中 j 是一定会从\(s_i\)之后的，因为是要粉刷包含s_i的木板，然后在\(j\)中枚举 \(k\)，有点类似于背包问题，感性理解，很显然。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
using namespace std;
const int maxn=16010;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){ if(ch == '-') f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0'; ch=getchar();}
return x*f;
}
int n,m;
struct People
{
int l,s,p;
}ren[maxn];
int f[120][maxn];
pair<int,int> q[maxn];
bool cmp(People x,People y)
{
return x.s<y.s;
}
int main()
{
n=read(),m=read();
for(int i=1;i<=m;i++)
{
ren[i].l = read();
ren[i].p = read();
ren[i].s = read();
}
sort(ren+1,ren+m+1,cmp);
for(int i=1;i<=m;i++)
{
int head = 1,tail = 0;
for(int j = 0; j<=n; j++)
{
f[i][j] = max(f[i-1][j],f[i][j-1]);
if(j >= ren[i].s)
{
while(head<=tail && q[head].second< j - ren[i].l) ++head;
if(head<=tail)
{
f[i][j] = max(f[i][j],q[head].first + ren[i].p * j);
}
}
else
{
while(head<=tail && q[tail].first <= f[i-1][j] - ren[i].p * j) tail--;
q[++tail].second = j;
q[tail].first = f[i-1][j] - ren[i].p *j;
}
}
}
printf("%d\n",f[m][n]);
return 0;
}
浙公网安备 33010602011771号