基环树

引言：

众所周知，\(N\)个点的树有\(N-1\)条边，若在树上随便加上一条边，也就是\(n\)条边，其中也就必然会有一个环，基环树也就是基于这种的树上，除了环之外，那必然是子树，同时将环中的一条边溢裂开，就会发现，也就是\(N-1\)条边的树，所以，在解决基环树的问题，解决的办法就是：

1.先找到环，

2.在环上溢裂一条边，形成数据结构树，在树上进行一系列操作，

3.进行信息合并。

基环树的内容：

1. 根据数据给定的图的连通性，我们也就是可以分为普通基环树和基环树森林，下面的例题就是属于基环树森林，一般情况下，不直接给出根，大部分就是基环树森林了的啦

2. 上面的隶属于无向图，那根据有向图呢？，我们可以分为三种，基环树，外向树和内向树

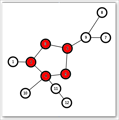
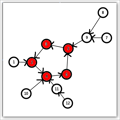
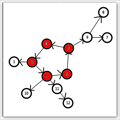
其中第一幅图就是基环树，无向图，第二幅就是内向树，每一个点有且只有一个出边。第三幅图就是外向树，有且只有一条入边。

求解的时候把环作为广义的“根节点”，把除了环之外的部分按照若干棵树处理

----------------------------------------我是分割线哇！------------------------------------------------------

【例题】：P2607[ZJOI2008]骑士

【题目分析】：

首先我真没看见有 \(n\)条边，然后发现，这就是个…… （没有上司的舞会），好，然后把没有上司的舞会改了改，交上去，好,RE。我发现题目不一样，然后发现，如果将一位骑士和他所憎恶的骑士连一条边，总共有\(n\)条边，然后应该意识到这是基环树了，毕竟基环树就是\(n\)条边嘛。

操作的话，就是先找到环，把环断开，形成一棵树，形成树之后我们的状态转移方程其实就是没有上司的舞会的状态转移方程，就很好办了。最后进行合并信息。然后找一遍环，跑一遍DP，唉，这不就\(OK\)了吗？想得挺美，这是个基环树森林，千看万看，没看出来。看了题解之后发现，想歪了。

【状态设计】：

\(f_{i,1}\)表示选择这位骑士最优解， \(f_{i,0}\)表示不选择这位骑士的最优解，状态设计类比一下没有上司的舞会就很好理解（需要理解？）

【状态转移】：

\(f_{now,1}=\sum\limits_{to \in son(i)}f_{to,0} + injury_{now}\)

\(f_{now,0}=\sum\limits_{to \in son(i)} max(f_{to,1},f_{to,0})\)

同样，对比一下，没有上司的舞会，算了，我直接把博客粘在这里,密码就是 123456789

【实现操作】：

我们在进行找环的时候进行DP,本来树是无向边的，但是我没过，类比我的没有上司的舞会， 我用了有向边，然后发现，用了有向边，再也不用担心会被卡无向二元环了（题解说的，反正我没有遇上）。傻人有傻福，，

【注意事项】（导致zzg裂开的罪魁祸首）：

1.在找环的时候，碰上 $ to == root$ 一定不能选，不选，不选

2.在输出的时候不要用 %d 用 long long 否则只有 70分，气死我了，交了5遍；

3.在建图的时候类比一下没有上司的舞会，别建反图

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <set>
#define int long long
using namespace std;
const int maxn=1000010;
struct Edge
{
	int nxt,to;
}edge[maxn<<1];
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
int number_edge,head[maxn<<1];
void add_edge(int from,int to)
{
	number_edge++;
	edge[number_edge].nxt=head[from];
	edge[number_edge].to=to;
	head[from]=number_edge;
}
int n;
int f[maxn][2];
int fight[maxn];//正经人都知道fight是干啥的； 
int vis[maxn],fa[maxn]; 
int ans,root;
void dp(int now)
{
	f[now][1]=fight[now];//这个点选择的话就是初始化本来的战斗力
	f[now][0]=0; // 不选择就是零，这个是森林，需要初始化
	vis[now]=1;
	for(int i=head[now];i;i=edge[i].nxt)
	{
		int to=edge[i].to;
		if(to == root) f[to][1]=-1; //由于这个地方没有管，导致zzg直接裂开， MLE,TLE,WA,RE 
		else 
		{
			dp(to);
			f[now][1]+=f[to][0];
			f[now][0]+=max(f[to][0],f[to][1]);
		}
		
	}
}
void find(int now)
{
	vis[now]=1;
	root=now;
	while(!vis[fa[root]])
	{
		root=fa[root];
		vis[root]=1;
	}
	dp(root);
	int ans1=f[root][0];
	root=fa[root];
	dp(root);
	ans1=max(ans1,f[root][0]);
	ans+=ans1;
}
signed main()
{ 
	n=read();
	for(int i=1;i<=n;i++)
	{
		fight[i]=read();
		int y=read();
		add_edge(y,i);
		fa[i]=y; // 一开始建反了图了 
	}
	for(int i=1;i<=n;i++)
	{
		if(!vis[i])
		{
			find(i);
		}
	}
	printf("%lld",ans);
	return 0;
}