2021.5.8-N皇后（回溯）

题目链接：https://leetcode-cn.com/problems/n-queens
题目描述：
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

题解：

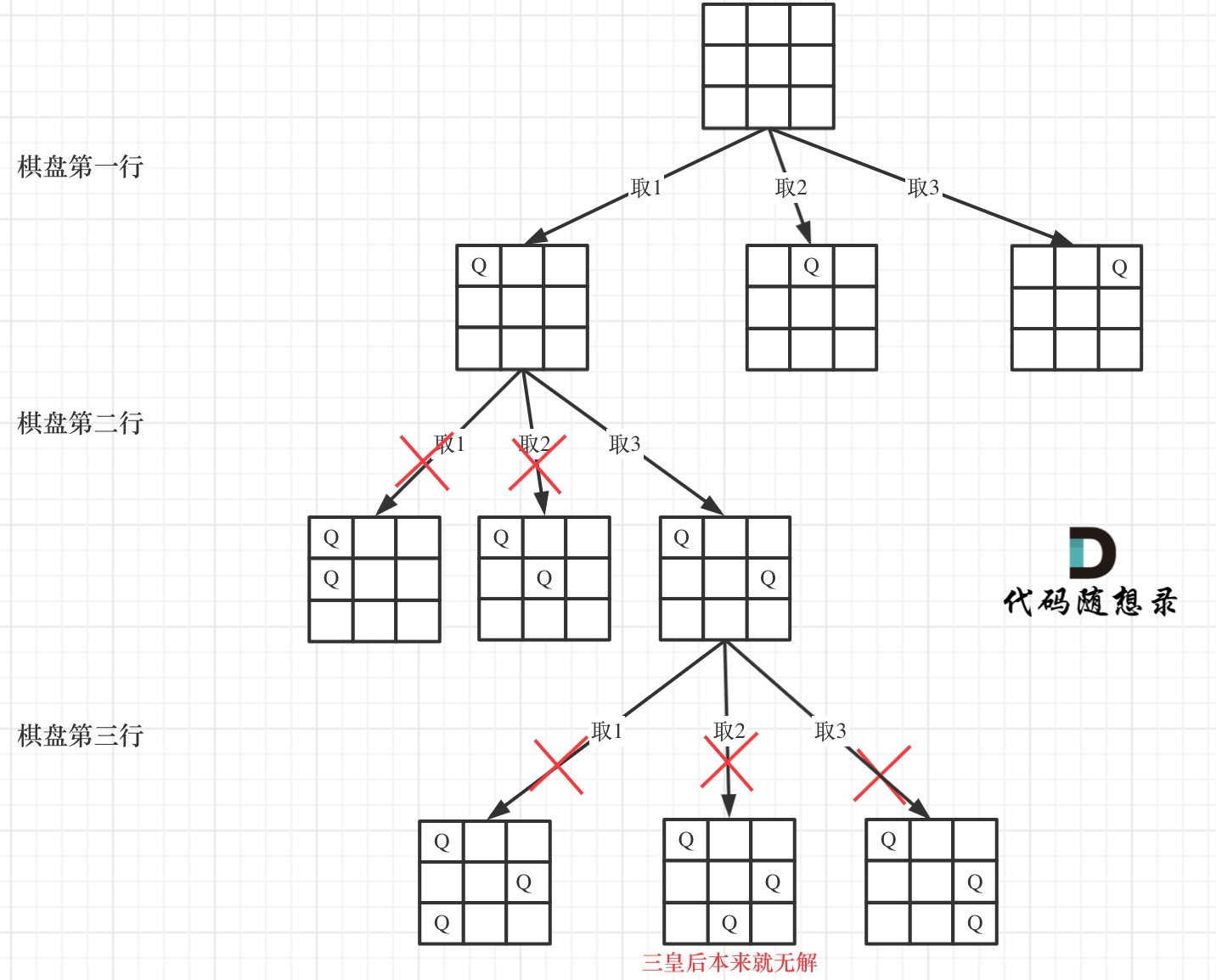
单层递归：
逐行放置[皇后]，只需检测新摆放[皇后]的列、左上对角、右上对角是否与已经摆放好的「皇后」有冲突。
递归深度就是row控制棋盘的行，每一层里for循环的col控制棋盘的列，一行一列，确定了放置皇后的位置。每次都是要从新的一行的起始位置开始搜，所以列都是从0开始。
如果发现有冲突，回溯皇后放置的位置。

class Solution {
private:
vector<vector<string>> result;
vector<string> chess;
public:
    bool isVaild(int row, int col, int n, vector<string>& chess)
    {
        //检查列
        for(int i = 0; i < row; i++)
        {
            if(chess[i][col] == 'Q')
                return false;
        }
        //检查135°方向
        for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++)
        {
            if(chess[i][j] == 'Q')
                return false;
        }
        //检查45°方向
        for(int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--)
        {
            if(chess[i][j] == 'Q')
                return false;
        }
        return true;
    }

    void backtracking(int n, int row, vector<string>& chess)
    {
        //最后一行已摆放完毕
        if(row == n)
        {
            result.push_back(chess);
            return;
        }
        //递归的宽度由col决定
        for(int col = 0; col < n; col++)
        {
            if(isVaild(row, col, n, chess))
            {
                chess[row][col] = 'Q';       //没有冲突，放置皇后
                backtracking(n, row + 1, chess);     //递归的深度由row决定
                chess[row][col] = '.';      //回溯
            }
        }
    }

    vector<vector<string>> solveNQueens(int n) {
        vector<string> chess(n, string(n, '.'));
        backtracking(n, 0, chess);
        return result;
       
    }
};