【MIT18.06·线性代数02】

线性方程组的矩阵形式

可以将线性方程组写成 \(Ax=b\) 的矩阵相乘形式：

比如线性方程组\(\left\{\begin{matrix} \begin{aligned} 2x-y&=0\\ -x+2y&=3 \end{aligned} \end{matrix}\right.\)可以写成矩阵形式\(\begin{bmatrix} 2 &-1 \\ -1 &2 \end{bmatrix} \begin{bmatrix}x \\y \end{bmatrix}= \begin{bmatrix}0 \\3 \end{bmatrix}\)

其中：

• \(A=\begin{bmatrix} 2 &-1 \\ -1 &2 \end{bmatrix}\)称为系数矩阵（Coefficients Matrix）
• \(x=\begin{bmatrix}x \\y \end{bmatrix}\)是未知数向量（Unknowns Vector）

线性方程组的几何解释

在线性方程组的矩阵形式的基础上，引入对线性方程组的两种几何解释：
1）Row Picture 行图像
2）Column Picture 列图像
这两种几何解释中所说的“行”和“列”实际上是指系数矩阵\(A\)中的行和列，在Row Picture中每次看\(A\)中的一行，在Column Picture中每次看\(A\)中的一列。

Row Picture 行图像

所谓行图像，就是每次看一行，比如\(\begin{bmatrix}2 &-1 \end{bmatrix} \begin{bmatrix}x \\y \end{bmatrix}=0\)；
一行对应一个线性方程，\(\begin{bmatrix}2 &-1 \end{bmatrix} \begin{bmatrix}x \\y \end{bmatrix}=0\)对应的就是线性方程组中的第一个方程\(2x-y=0\)；
在坐标轴中画出每一行对应的图像，含有2个未知量的线性方程在坐标轴中是一条直线，含有3个未知量的是一个平面...，比如画出\(\left\{\begin{matrix} \begin{aligned} 2x-y&=0\\ -x+2y&=3 \end{aligned} \end{matrix}\right.\)的每一行就得到下图所示的图像：

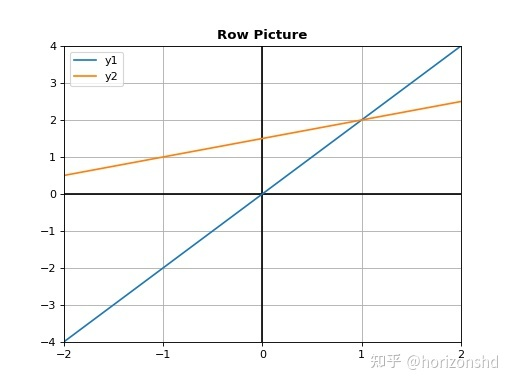
图中两条直线的交点\((2,1)\)对应于线性方程组的解。

Column Picture 列图像

所谓列图像就是每次看一列，比如在系数矩阵\(A=\begin{bmatrix} 2 &-1 \\ -1 &2 \end{bmatrix}\)包含两列\(\begin{bmatrix}2 \\-1 \end{bmatrix}\)和\(\begin{bmatrix}-1 \\2 \end{bmatrix}\)，它们分别对应于线性方程组中未知量\(x\)的系数和未知量\(y\)的系数，可以将每一个未知数的系数放在一起看作一个向量，那么求解线性方程组\(\left\{\begin{matrix} \begin{aligned} 2x-y&=0\\ -x+2y&=3 \end{aligned} \end{matrix}\right.\)的过程就可以看作是求解一个对于列向量\(\begin{bmatrix}2 \\-1 \end{bmatrix}\)和\(\begin{bmatrix}-1 \\2 \end{bmatrix}\)的“合适”的线性组合的过程，所谓“合适”是指可以刚好使得 \(x\begin{bmatrix}2\\-1\end{bmatrix}+y\begin{bmatrix}-1\\3\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}\)。

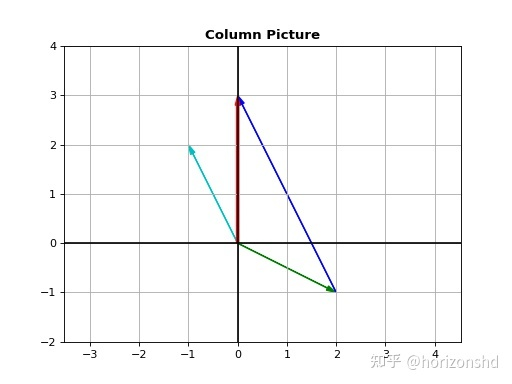
绘制列图像

1. 在坐标系中画出系数矩阵\(A\)的每一个列向量，比如下图中的青色\(\begin{bmatrix}2 \\-1 \end{bmatrix}\)和绿色\(\begin{bmatrix}-1 \\2 \end{bmatrix}\)两个向量；
2. 然后再画出目标向量\(b\)，比如图中的红色向量\(\begin{bmatrix}0 \\3\end{bmatrix}\)；
3. 此时，线性方程组的解\((2,1)\)对应于系数矩阵\(A\)的列向量的一个线性组合 \(2\begin{bmatrix}2\\-1\end{bmatrix}+1\begin{bmatrix}-1\\3\end{bmatrix}\)，图中的紫色向量是\(2\begin{bmatrix}2\\-1\end{bmatrix}\)，绿色向量就是\(1\begin{bmatrix}-1\\3\end{bmatrix}\)，这两个向量矢量相加之后正好就是目标向量\(b\)（红色向量）。
   

矩阵与向量相乘

\(Ax\)正好是一个矩阵\(A\)右乘一个向量\(x\)，与行向量/列向量相对应的，有两种看待矩阵与向量相乘的方式：
1）一次看一行
2）一次看一列

【例】求矩阵与向量相乘的结果：\(\begin{bmatrix} 2 &5 \\ 1 &3 \end{bmatrix} \begin{bmatrix}1 \\2 \end{bmatrix}\)

一次看一行

以此引出向量点乘：

1. \(\begin{bmatrix} 2 &5 \end{bmatrix} \cdot \begin{bmatrix}1 \\2 \end{bmatrix}=2 \times1+5\times2=12 \)
2. \(\begin{bmatrix} 1 &3 \end{bmatrix} \cdot \begin{bmatrix}1 \\2 \end{bmatrix}=1 \times1+3\times2=7 \)

计算结果为\(\begin{bmatrix}2 \times1+5\times2 \\1 \times1+3\times2 \end{bmatrix}=\begin{bmatrix}12\\7 \end{bmatrix}\)

一次看一列

\(Ax\)可以看作矩阵\(A\)的列向量的线性组合，向量\(x\)中对应每一个列向量在线性组合中的系数：

\[\begin{bmatrix} 2 &5 \\ 1 &3 \end{bmatrix} \begin{bmatrix}1 \\2 \end{bmatrix}=1\begin{bmatrix}2\\1 \end{bmatrix}+2\begin{bmatrix}5\\3 \end{bmatrix}=\begin{bmatrix}2 \times1+5\times2 \\1 \times1+3\times2 \end{bmatrix}=\begin{bmatrix}12\\7 \end{bmatrix}\]