【机器学习的数学02】数列的极限
数列的极限
本文为基于 “《机器学习的数学》- 第1章 一元函数微积分 - 1.1 极限与连续 - 1.1.2 数列的极限” 的学习笔记
知识脉络梳理:
- 给出数列极限的定义:
- 直观理解
- \(\epsilon\)定义
- 数列极限的四则运算
- 证明数列极限存在:
- 用定义证明
- 单调收敛定理
- 夹逼定理
一、数列极限的定义
【定义1】对于数列\({a_n}\)以及某一实数\(a\),如果对于任意给定的\(\epsilon > 0\)都存在正整数\(N\),使得对于任意满足\(n>N\)的\(n\)都有下面的不等式成立
\[|a_n-a|<\epsilon \]则称此数列\({a_n}\)的极限为\(a\),或称其收敛于\(a\),记为
\[\lim\limits_{n\rightarrow+\infty} \quad a_n \]如果数列的极限不存在,则称该数列发散。
直观理解:当\(n\)增加时数列的值\(a_n\)无限接近于\(a\),可以接近到任意指定的程度(由\(\epsilon\)控制)。
如何理解数列极限的定义? - 知乎用户的回答 - 知乎 https://www.zhihu.com/question/347024216/answer/831202633
二、数列极限的四则运算

三、数列极限的证明
3.1 适用数列极限的定义证明
【例1】

3.2 单调收敛定理
3.2.1 数列上界与下界

3.2.2 单调收敛定理
单调收敛定理: 单调有界 -> 收敛。
- 单调递增有上界 -> 收敛
- 单调递减有下界 -> 收敛
在单调收敛定理中一共有三个组成因素:单调、有界和收敛,下面对这三个因素之间的关系作详细讨论:
- 单调 & 收敛:单调与收敛没有必然联系
- 有界 & 收敛:有界是收敛的必要不充分条件
- 有界不一定收敛,比如\(\{(-1)^n\}\)
- 收敛一定有界
- 如果一个数列的极限是a,那么下标很大的那些项,离a就很近,可以想象到,从某一项开始,之后的每一项都分布在a的某个很小的邻域内(由\(\epsilon\)指定),再加上前面的有限项,整体必然是有界的
- 有界+单调 & 收敛:单调有界是收敛的充分不必要条件
- 单调有界一定收敛
- 收敛不一定单调有界,比如\(\{ \ \frac{(-1)^n}{n} \ \}\)
重要极限:\(\lim\limits_{n\rightarrow\infty} \ (1+\frac{1}{n})^n = e\)
【例2】证明数列\(a_n=\{ (1+\frac{1}{n})^n \}\)的极限存在。

综上所述:数列\(a_n=\{ (1+\frac{1}{n})^n \}\)单调递增有上界,根据单调收敛定理,该数列的极限存在。
重要极限:\(\lim\limits_{n\rightarrow\infty} \ (1-\frac{1}{n})^n = \frac{1}{e}\)
该极限在概率论中的含义是:对n个样本进行n次有放回等概率抽样,当样本数趋于无穷大时,某个样本一次都没抽中的概率,该极限在随机森林算法中会用到。
或者理解为:有n个编号从1到n的小球,每次抽一个小球,抽完放回,一共进行n次试验;对于编号为\(i, 1\leq i \leq n\)的小球,在每一次抽取时抽到它的概率是\(\frac{1}{n}\),抽不到它的概率是\(1-\frac{1}{n}\);在n次抽样中每一次都抽不到编号为i的小球的概率是\((1-\frac{1}{n})^n\);当n趋向于无穷大时,每一次都抽不到编号为i的小球的概率是\(\frac{1}{e}\)。
【例3】计算数列\(\{ (1-\frac{1}{n})^n \}\)的极限

3.3 夹逼定理
夹逼定理:对于\(\forall n \in \mathbb{N}\)有\(b_n \leq a_n \leq c_n\)且\(\lim\limits_{n\rightarrow\infty}b_n = \lim\limits_{n\rightarrow\infty}c_n = c\),则\(\lim\limits_{n\rightarrow\infty}a_n = c\)。
重要极限:\(\lim\limits_{p\rightarrow\infty} \ (\sum_{i=1}^n \ |x_i|^p \ )^{\frac{1}{p}} = max|x_i|\)
该极限对应于向量的\(+\infty\)范数。
【例4】假设\(x_i\)不全为0,计算极限\(\lim\limits_{p\rightarrow\infty} \ (\sum_{i=1}^n \ |x_i|^p \ )^{\frac{1}{p}}\)

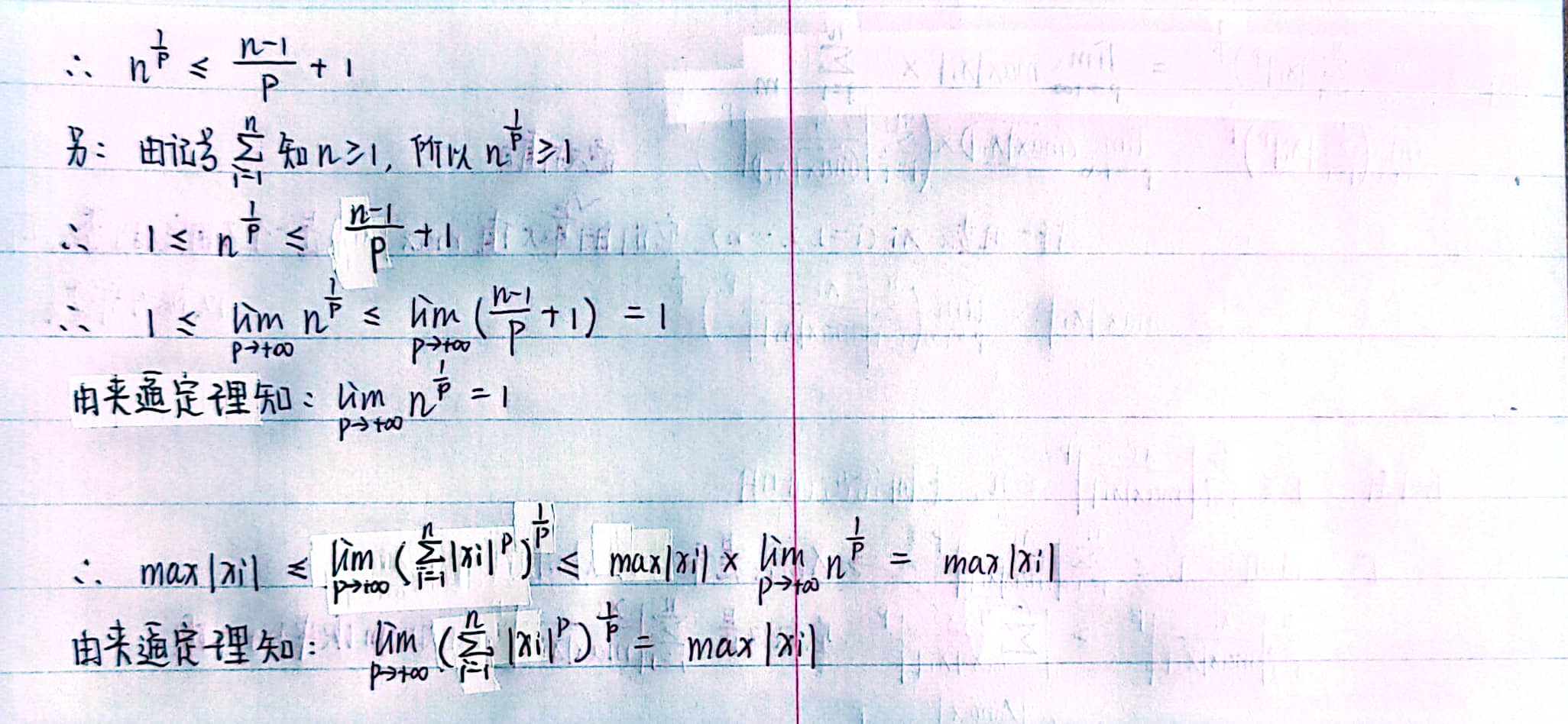



 浙公网安备 33010602011771号
浙公网安备 33010602011771号