10 二叉搜索树
1. 验证二叉搜索树

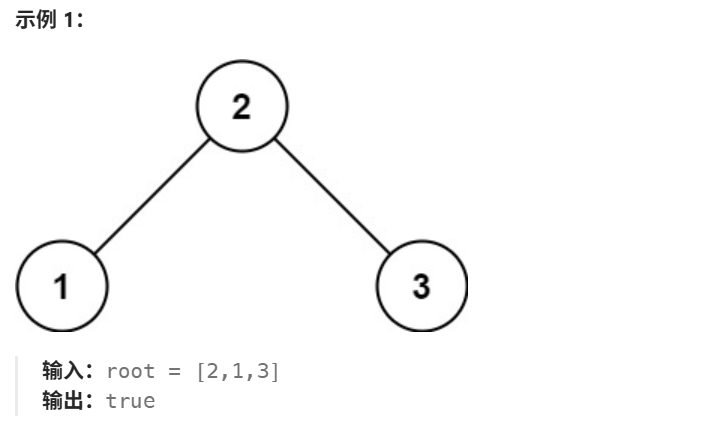
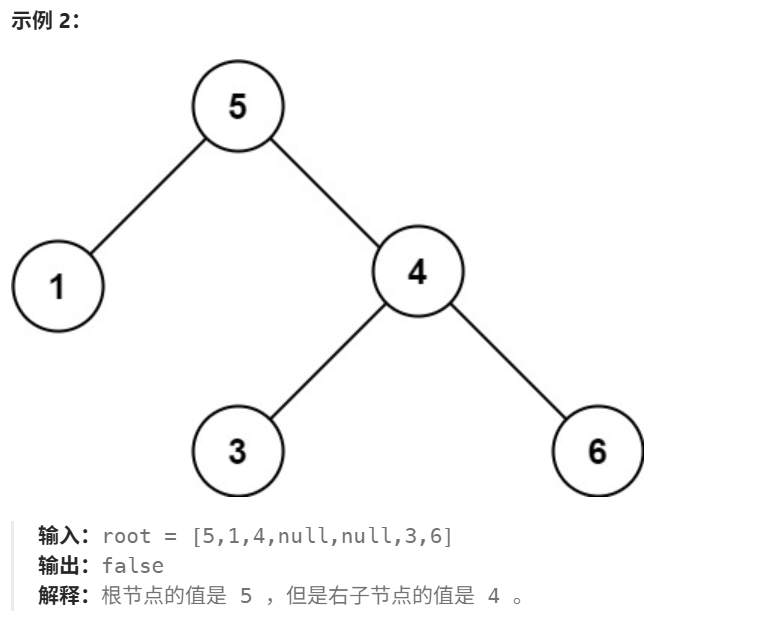
1.1 解题思路
1.1.1 方法一:前序遍历
根据定义,二叉树的左右子树一定也是二叉搜索树。
因此:
原问题:判断一棵树是否是二叉搜索树
子问题:判断一棵树的左子树/右子树是否是二叉搜索树
在递归时,除了传入节点,还需要传入该节点所处开区间的范围。
对于每个节点,先判断它的节点值是否在开区间内,然后再往下递归。
如果递归到左子结点,那就更新开区间的右边界为节点值;
如果递归到右子节点,就更新开区间的左边界为节点值;
像这种先访问节点值再递归左右子树的做法,叫做前序遍历。
1.1.2 方法二:中序遍历
如果按照“左根右”,递归左子树,访问根节点值,再递归右子树,这样的顺序遍历,将会得到一个递增的数组。
遍历完左子树,我们就可以看当前的值是否严格大于上一个节点的值,然后再记录下当前节点的值,用于递归时与下一个节点进行比较。
1.1.3 方法三:后序遍历
把节点值的范围往上传,先遍历左右子树。如果判断当前节点大于左子树的最大值而且小于右子树的最小值,那么认为这是合法的。
看上去左边只需要返回一个最大值,右边只需要返回最小值即可。(最小值和最大值都需要返回)
1.2 代码实现
1.2.1 方法一:前序遍历
点击查看代码
class Solution {
public:
bool isValidBST(TreeNode* root, long long left = LLONG_MIN, long long right = LLONG_MAX) {
if (root == nullptr) {
return true;
}
long long val = root->val;
return val > left && val < right &&
isValidBST(root->left, left, val) &&
isValidBST(root->right, val, right);
}
};
1.2.2 方法二:中序遍历
点击查看代码
class Solution {
long long pre = LLONG_MIN;
public:
bool isValidBST(TreeNode* root) {
if (root == nullptr) {
return true;
}
if (!isValidBST(root->left)) {
return false;
}
if (root->val <= pre) {
return false;
}
pre = root->val;
return isValidBST(root->right);
}
};
1.2.3 方法三:后序遍历
点击查看代码
class Solution {
public:
bool isValidBST(TreeNode* root) {
long long right = LLONG_MAX;
long long left = LLONG_MIN;
auto dfs = [&](this auto&&dfs, TreeNode* root) ->pair<long long, long long> {
if (root == nullptr) {
return {right, left};
}
auto [l_min, l_max] = dfs(root->left);
auto [r_min, r_max] = dfs(root->right);
long long val = root->val;
if (val <= l_max || val >= r_min) {
return {left, right};
} // 因为空节点时返回的是{inf, -inf}
return {min(l_min, val), max(r_max, val)};
};
return dfs(root).second != right;
}
};
- 时间复杂度:$$O(n)$$
- 空间复杂度:$$O(n)$$
2 二叉树的最近公共祖先
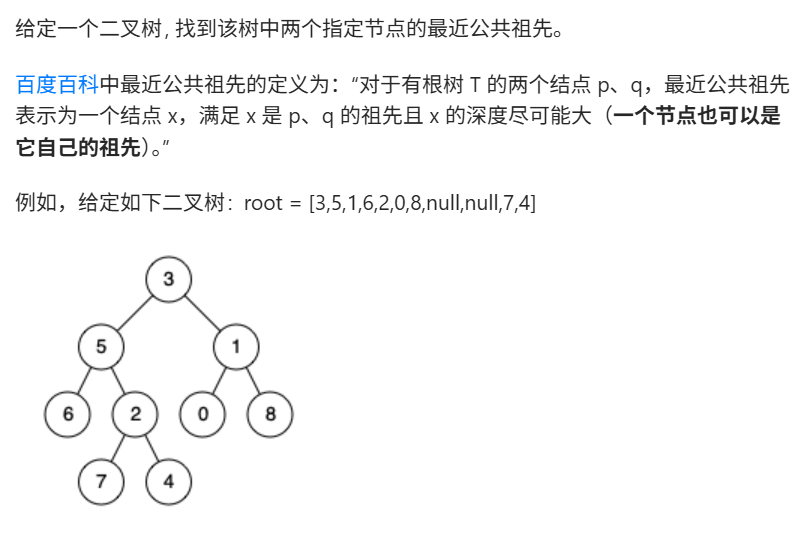

2.1. 解题思路
给你一棵二叉树,以及这棵树上的两个节点\(p\)和\(q\),要怎么找到\(p\)和\(q\)的最近公共祖先呢?
递归到当前节点,分类讨论
1.当前节点是空节点:直接返回空节点
2.当前节点是\(p\):不需要继续往下递归了,直接返回\(p\)。原因是:
- 无论\(q\)是\(p\)左子树中的一个节点还是\(p\)右子树中的一个节点,最近公共祖先都是\(p\)
- 或者说\(p\)在左子树,\(q\)在右子树,这种情况下也不需要继续往下递归
3.当前节点是\(q\):同2
4.其他情况:是否找到\(p\)和\(q\)
- \(p\)和\(q\)分别在左右子树中:最近公共祖先就是当前节点,因此返回当前节点
- \(p\)和\(q\)都在左子树中:最近公共祖先一定在左子树中,返回左子树的递归结果
- \(p\)和\(q\)都在右子树中:返回右子树的递归结果
- 没有找到\(p\)和\(q\):返回空
2.2. 代码实现
点击查看代码
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == nullptr || root == p || root == q) {
return root;
}
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if (left != nullptr && right != nullptr) {
return root;
}
if (left != nullptr)
return left;
if (right != nullptr)
return right;
return nullptr;
}
};
- 时间复杂度:$$O(n)$$
- 空间复杂度:$$O(n)$$
小结:一点也不简单
3. 二叉搜索树的最近公共祖先
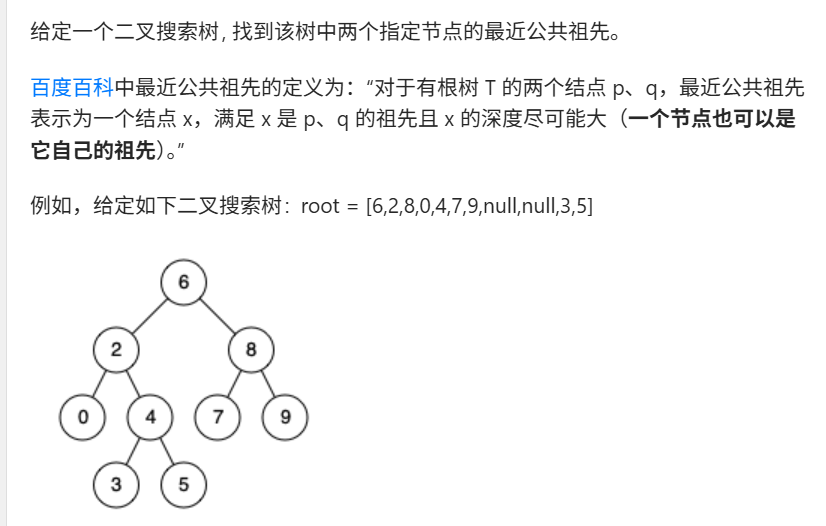

3.1. 解题思路
二叉搜索树的性质:左子树的节点值都比根节点值小,右子树的节点值都比根节点值大。
如果\(p\)和\(q\)的节点值都小于当前的节点值,那么\(p\)和\(q\)(如果有)一定在当前节点的左子树中;(\(p\)和\(q\)都在左子树,返回左子树的递归结果)
同理,如果\(p\)和\(q\)的节点值都大于当前的节点值,那么\(p\)和\(q\)(如果有)一定在当前节点的右子树中。(\(p\)和\(q\)都在右子树,返回右子树的递归结果)
其他情况:
- \(p\)和\(q\)分别在左右子树中,那么返回递归的当前节点。
- 当前节点是\(p\)或者\(q\),直接返回当前节点。
最后,由于题目保证\(p\)和\(q\)都在树中,那么根节点一定不是空节点。所以不需要判断空节点。
3.2. 代码实现
点击查看代码
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
int val = root->val;
if (p->val < val && q->val < val) {
return lowestCommonAncestor(root->left, p, q);
} else if (p->val > val && q->val > val) {
return lowestCommonAncestor(root->right, p, q);
}
return root;
}
};
- 时间复杂度:$$O(n)$$
- 空间复杂度:$$O(n)$$
4. 二叉树的层序遍历
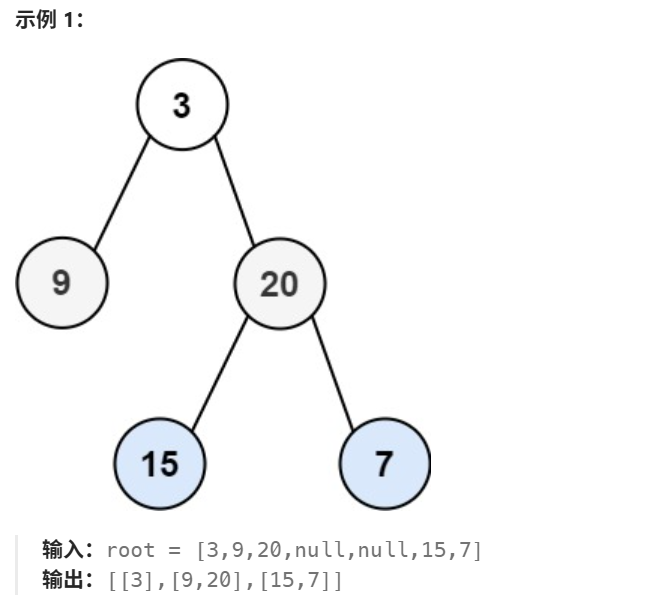
4.1 解题思路
4.1.1 法一(双数组):
创建一个初始数组current,把根节点放进去。进入循环,创建一个nxt数组。遍历current数组中的每个节点,将其左右孩子都放入nxt数组中。于是,遍历完current之后,我们就得到了下一层节点的值。
4.1.2 队列:
4.2 代码实现
4.2.1 法一(双数组):
点击查看代码
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if (root == nullptr) {
return {};
}
vector<vector<int>> ans;
vector<TreeNode*> cur;
vector<TreeNode*> nxt;
cur.push_back(root);
while (!cur.empty()) {
vector<int> temp;
int size = cur.size();
for (int i = 0; i < size; ++i) {
temp.push_back(cur[i]->val);
if (cur[i]->left != nullptr) {
nxt.push_back(cur[i]->left);
}
if (cur[i]->right != nullptr) {
nxt.push_back(cur[i]->right);
}
}
ans.push_back(std::move(temp));
cur = std::move(nxt);
}
return ans;
}
};
- 时间复杂度:$$O(n)$$
- 空间复杂度:在每一层都填满的情况下,也即满二叉树。第\(1\)层\(2^0,那么第\)h$层就有\(2^{h-1}\)个节点,总节点数为\(2^h-1=n\),得到第\(h\)大约最多有\(\frac{n+1}{2}\)个节点。所以空间复杂度为\(O(n)\)。
4.2.2 法二:优先队列
点击查看代码
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
// 队列
if (root == nullptr) {
return {};
}
vector<vector<int>> ans;
queue<TreeNode*> que;
que.push(root);
while (!que.empty()) {
vector<int> value;
int size = que.size();
for (int i = 0; i < size; ++i) {
auto node = que.front();
que.pop();
value.push_back(node->val);
if (node->left != nullptr) {
que.push(node->left);
}
if (node->right != nullptr) {
que.push(node->right);
}
}
ans.push_back(std::move(value));
}
return ans;
}
};
5 锯齿形层序遍历
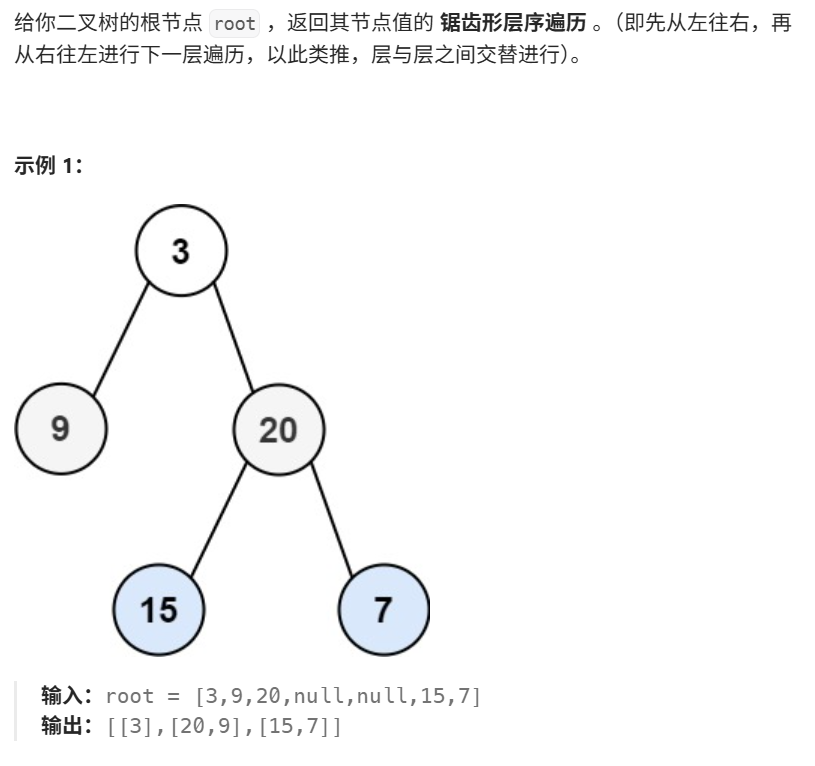
5.1. 代码实现
点击查看代码
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
// 队列
// 偶数层需要翻转一下数组。因为需要知道当前层是偶数层还是奇数层,所以用一个bool变量
if (root == nullptr) {
return {};
}
vector<vector<int>> ans;
queue<TreeNode*> que;
que.push(root);
bool even = false; // 一开始是奇数层
while (!que.empty()) {
vector<int> value;
int size = que.size();
for (int i = 0; i < size; ++i) {
auto node = que.front();
que.pop();
value.push_back(node->val);
if (node->left != nullptr) {
que.push(node->left);
}
if (node->right != nullptr) {
que.push(node->right);
}
}
if (even) {
reverse(value.begin(), value.end());
}
ans.push_back(std::move(value));
even = !even;
}
return ans;
}
};
6 找树左下角的值
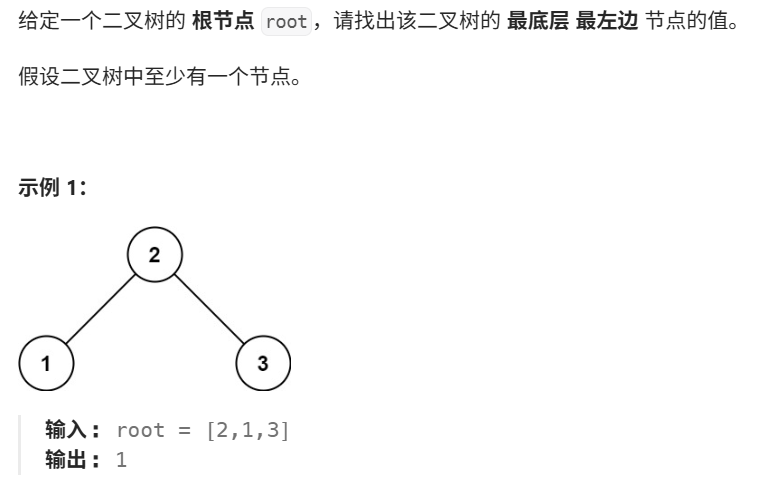
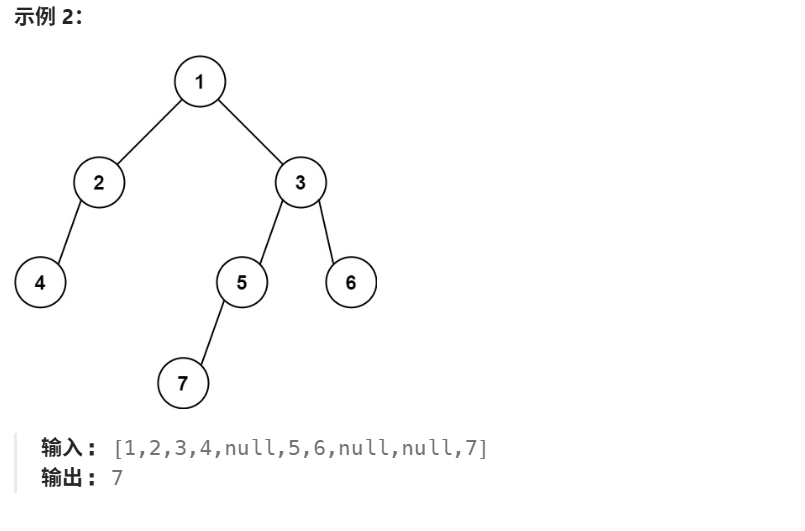
6.1 解题思路
依旧是层序遍历的思路。如果按照从左往右的顺序,那么就是记录每层遍历到的第1个节点。如果是从右往左的顺序,那么就是记录每层遍历到的最后1个节点。
6.2 代码实现
点击查看代码
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
// 队列
if (root == nullptr) {
return {};
}
int ans = 0;
queue<TreeNode*> que;
que.push(root);
while (!que.empty()) {
auto node = que.front();
que.pop();
ans = node->val;
if (node->right != nullptr) {
que.push(node->right);
}
if (node->left != nullptr) {
que.push(node->left);
}
}
return ans;
}
};
- 时间复杂度:$$O(n)$$
- 空间复杂度:$$O(n)$$


 浙公网安备 33010602011771号
浙公网安备 33010602011771号