09 二叉树 & 递归

1. 计算二叉树的最大深度

1.1. 解题思路

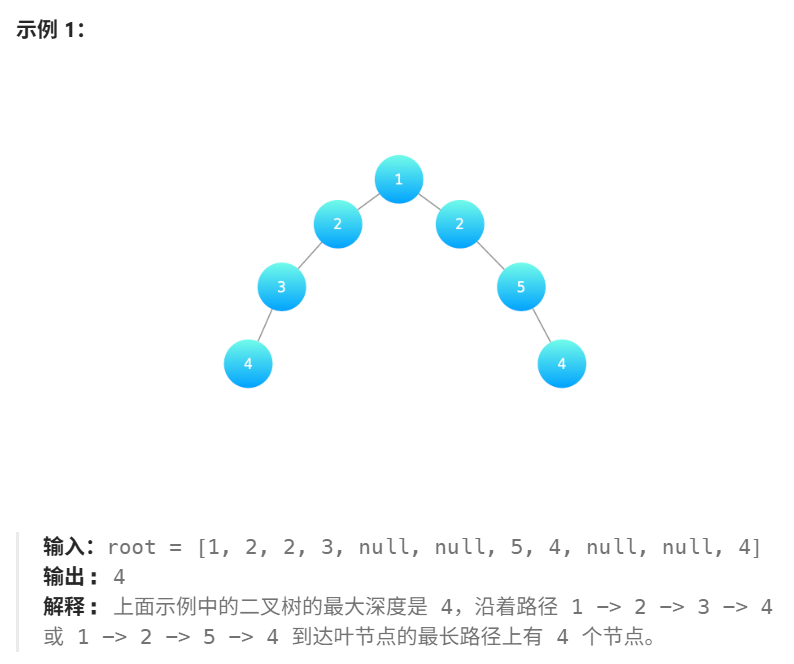
所谓二叉树的深度，指的是从根节点到最远叶子结点的最长路径上节点的个数。
思考整棵树与左右子树的关系。
整棵树的最大深度 = \(max\)(左子树的最大深度，右子树的最大深度) + 1

原问题：计算整棵树的最大深度
子问题：计算左/右子树的最大深度

程序执行循环的过程是在重复执行同样一份代码，因此这里计算子问题和原问题也应当使用同一份代码。
这里和循环的区别在于，如循环遍历数组，计算一个数组的元素和，做法是用一个循环外的变量，不断累加数组中的元素更新循环外的变量。而这里的问题存在嵌套关系：我们需要我们的计算结果返回给上一级。

递归的【递】，就是子问题的规模比原问题小，需要不断往下【递】，总会有个尽头：即递归的边界条件，此时直接返回它的答案【归】。

针对这个问题，当遇到空节点时，我们可以直接返回0，这个返回的过程就是【归】。

1.2. 代码实现

1.2.1. 第1种做法

点击查看代码

class Solution {
public:
    int calculateDepth(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        return max(calculateDepth(root->left), calculateDepth(root->right)) + 1;   
    }
};

• 时间复杂度：$$O(n)$$ 每个节点我们都遍历了一次
• 空间复杂度：$$O(n)$$ 最差情况下，二叉树退化成链表，需要$$O(n)$$的栈帧空间

1.2.2. 第2种做法

点击查看代码

class Solution {
public:
    int calculateDepth(TreeNode* root) {
        int ans = 0;
        // node 当前经过的节点
        // cnt 当前经过的节点个数
        auto dfs = [&](this auto&&dfs, TreeNode* node, int cnt) {
            if (node == nullptr) {
                return;
            }
            cnt += 1;
            ans = max(ans, cnt);
            dfs(node->left, cnt);
            dfs(node->right, cnt);
        };
        dfs(root, 0);  
        return ans;  
    }
};

• 时间复杂度：$$O(n)$$
• 空间复杂度：$$O(n)$$

注：第2种做法将路径上的节点个数也传下去

2. 相同的树

2.1. 解题思路

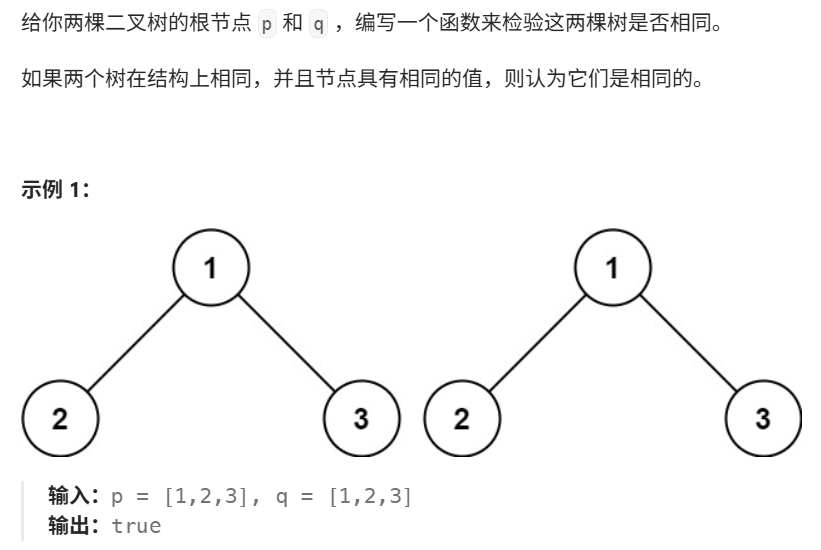
如何判断两棵树是相同的呢？
对于两棵树而言，如果它们的左右子树都相同，且根节点上的值也相同，那么这两棵树才被认为是相同的。

原问题：两棵树是否是相同的
子问题：两棵树的左子树/右子树是否是相同的

不断递归总会有个尽头，边界条件是什么呢？
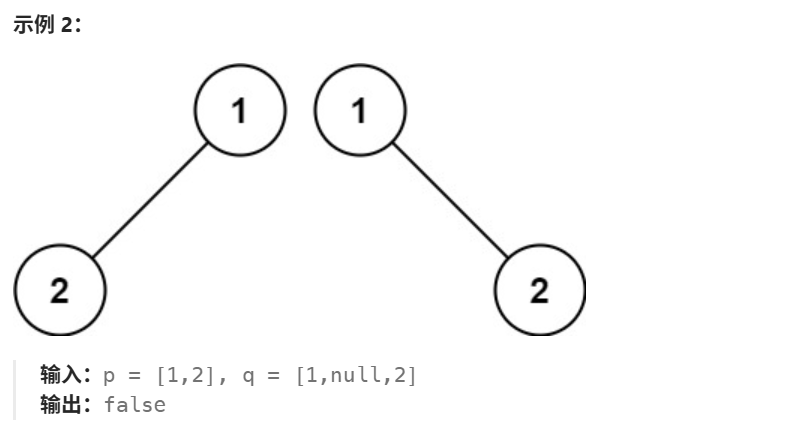
如果传进去的两个节点有一个是空的，那么就无法进行递归了，也即需要进行判断。

• 如果两个节点都是空，就返回true
• 否则就返回false

2.2. 代码实现

2.2.1. 灵神的做法

点击查看代码

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if (p == nullptr || q == nullptr) {
            return p == q; // 只要有一个节点为空，便不能往下【递】
        } // 只有 p和q同时为空才会返回 true
        return p->val == q->val && isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }
};

2.2.2. 我写的

点击查看代码

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if (p == nullptr && q == nullptr) {
            return true;
        } else if (p != nullptr && q == nullptr) {
            return false;
        } else if (p == nullptr && q != nullptr) {
            return false;
        } else if (p->val != q->val) {
            return false;
        }
        return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }
};

• 时间复杂度：$$O(n)$$
• 空间复杂度：$$O(n)$$

3. 对称二叉树

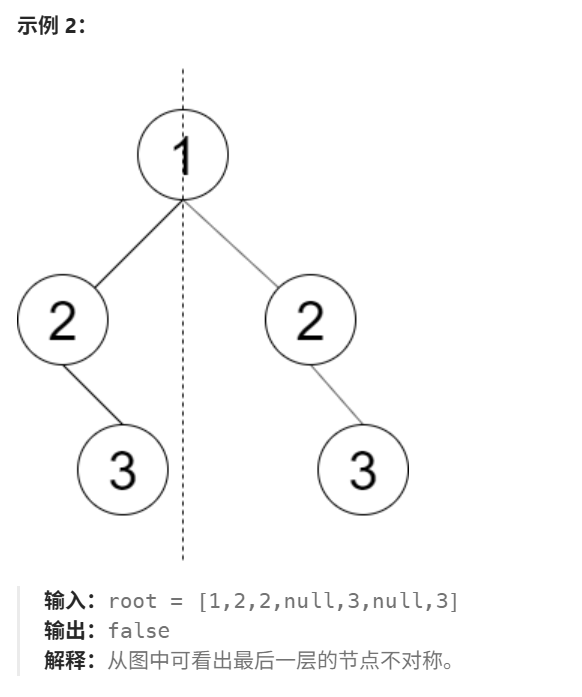
3.1. 解题思路

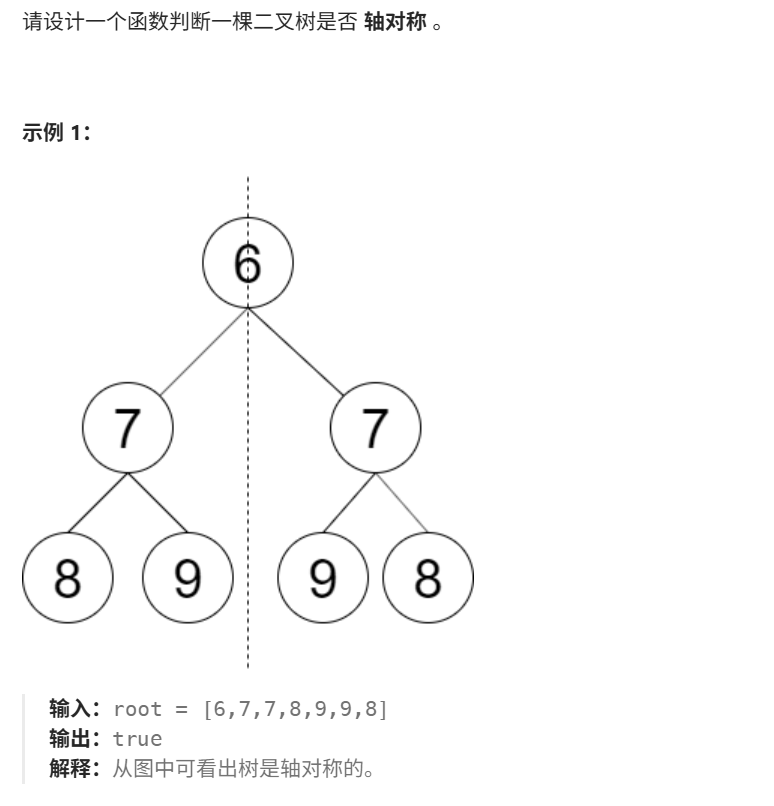
给你一棵二叉树，如何判断其是否轴对称？
沿用上一道题的思路，其中，根节点是一样的，那么同时递归左右两棵子树。

3.2. 代码实现

点击查看代码

class Solution {
public:
    bool checkSymmetricTree(TreeNode* root) {
        auto isSame = [&](this auto&& isSame, TreeNode* p, TreeNode* q) -> bool {
            if (p == nullptr || q == nullptr) {
                return p == q;
            }
            return p->val == q->val && isSame(p->left, q->right) && isSame(p->right, q->left);
        };
        if (root == nullptr) {
            return true;
        }
        return isSame(root->left, root->right);
    }
};

• 时间复杂度：$$O(n)$$
• 空间复杂度：$$O(n)$$

4 平衡二叉树

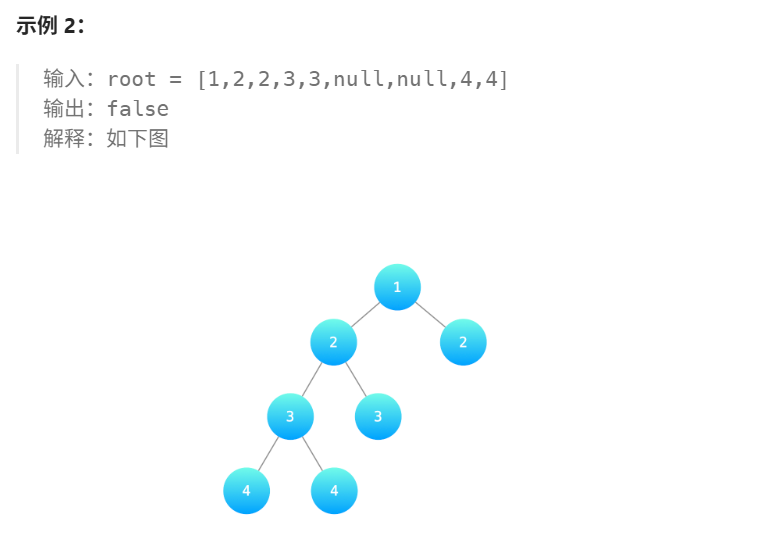
4.1. 解题思路

什么是深度？

• 从当前节点往下，到最远叶子结点的路径上的节点个数。例如示例\(1\)中根节点的左子树深度为1，右子树深度为2，所以返回true。

如何递归呢？
如果一个二叉树是高度平衡的，那么它的左右子树也是高度平衡的。这样原问题和子问题就有了。

【递】的过程，就是我们要不断判断左子树和右子树是不是满足平衡二叉树的性质。也即对一棵树，查询它的左子树高度和右子树高度。
如果递归半途中已经发现某颗左子树不满足性质了，那就返回-。原因是二叉树的高度都是正数，一旦返回负数就说明已经可以不用判断了，遂一路返回。

4.2. 代码实现

点击查看代码

class Solution {
public:
    bool isBalanced(TreeNode* root) {
        auto getHeight = [&](this auto&&getHeight, TreeNode* root) -> int {
            if (root == nullptr) {
                return 0;
            }
            int l_height = getHeight(root->left);
            if (l_height == -1) {
                return -1;
            }
            int r_height = getHeight(root->right);
            if (r_height == -1 || abs(l_height - r_height) > 1) {
                return -1;
            }
            return max(l_height, r_height) + 1;
        };
        if (root == nullptr) {
            return true;
        }
        return getHeight(root) == -1 ? false: true;
    }
};

• 时间复杂度：$$O(n)$$
• 空间复杂度：$$O(n)$$

5. 二叉树的右视图

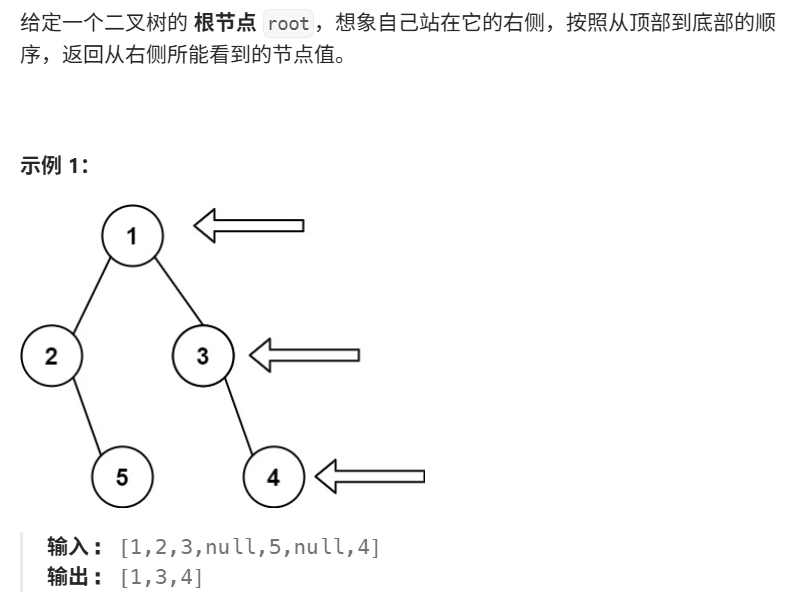
5.1. 解题思路

1. 这道题可以用层序遍历来做，将每层的最后一个节点存到返回的数组中。

2. 因为是找右视图，所以先递归右子树，再递归左子树。

问题1：如何把答案记下来？

• 传进去一个数组，或者将数组设为全局变量，需要的时候更新即可。

问题2：如何判断这个节点需要被记下来？

• 在递归的同时记录路径长的节点个数或是递归深度，如果说递归深度=答案的长度，比如刚开始数组长度为0，递归深度也为0，就把root记录下来。

5.2. 代码实现

点击查看代码

class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> ans;
        auto dfs = [&](this auto&&dfs, TreeNode* root, int depth) {
            if (root == nullptr) {
                return;
            }
            if (depth == ans.size()) {
                ans.push_back(root->val);
            }
            dfs(root->right, depth + 1);
            dfs(root->left, depth + 1);
        };
        dfs(root, 0);
        return ans;
    }
};

- 时间复杂度：$$O(n)$$
- 空间复杂度：$$O(n)$$