06 快慢指针

1 链表的中间结点

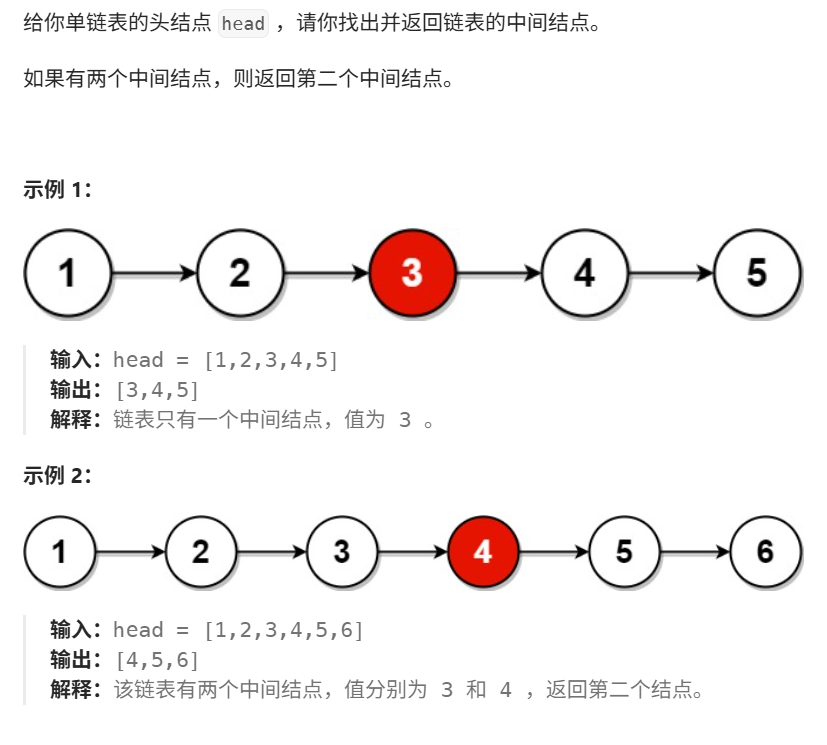
1.1 代码实现

点击查看代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        ListNode* slow = head, *fast = head;
        while (fast != nullptr && fast->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
        }
        return slow;    
    }
};

- 时间复杂度：$$O(n)$$ - 空间复杂度：$$O(1)$$

2 环形链表

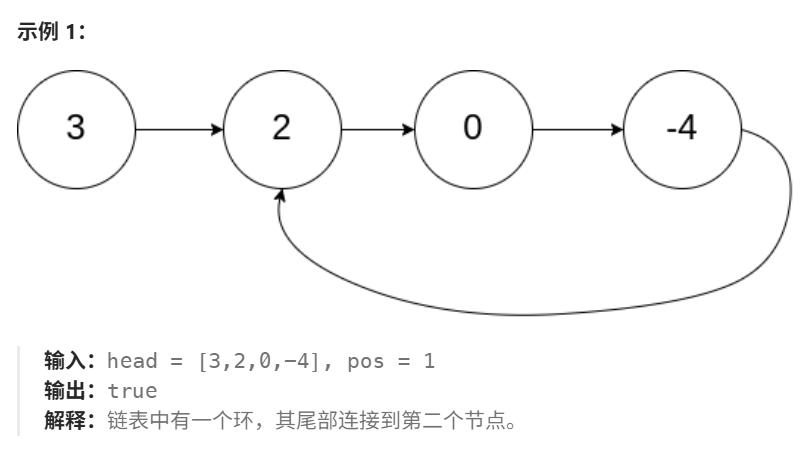
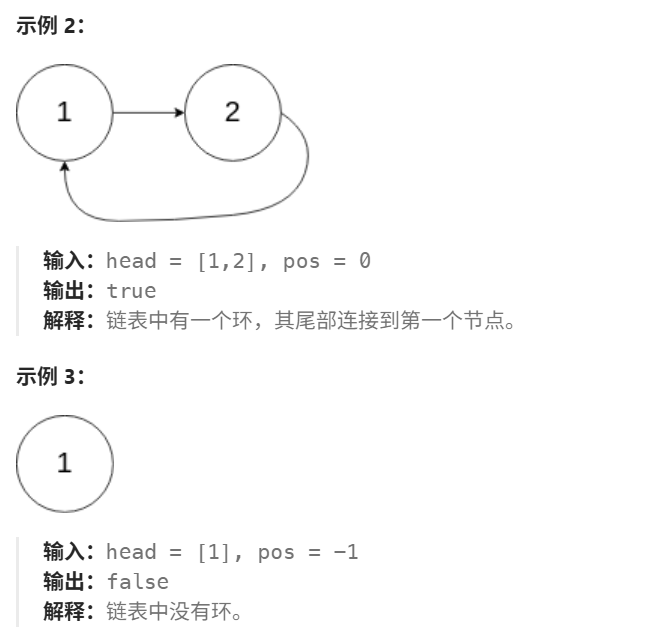
2.1 代码实现

点击查看代码

class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode* slow = head, * fast = head;
        while (fast != nullptr && fast->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow) {
                return true;
            }
        }
        // 如果有环，慢指针和快指针一定在环中的某个节点相遇
        return false;
    }
};

• 时间复杂度：$$O(n)$$
• 空间复杂度：$$O(1)$$

3 环形链表 II

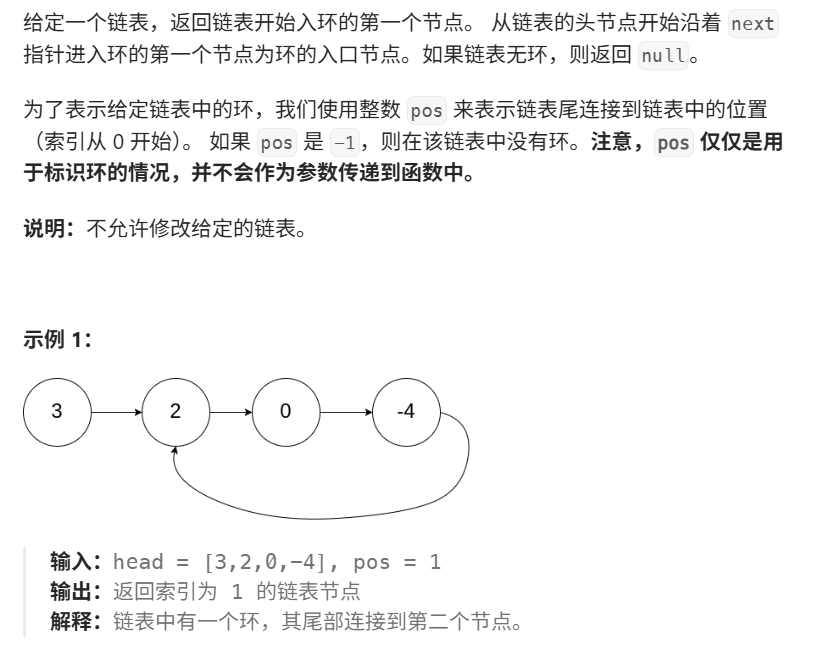
3.1 解题思路

3.1.1 计算环的长度（环有多少个节点）

在这道题中，我们不仅要判断链表是否有环，还要找到环的入口节点。
首先，如果有环，那么快慢指针一定在环中的某个节点处相遇。我们将这个节点做个标记。
我们想知道这个环到底有多少个节点。
假设环有n个节点，那么再次令快慢指针指向头结点，快指针先走n步，然后两个指针以相同的速度向前移动。
当慢指针指向环的入口时，快指针已经围绕着环走了一圈，二者相遇在入口节点。

3.1.2 不用计算环长

假设环长等于b + c，
慢指针移动距离等于a + b
快指针移动距离等于a + b + k(b + c)

由于快指针移动距离，是慢指针的两倍，所以有

\[2(a + b) = a + b + k(b + c) \]

\[2a + 2b = a + b + b + c + (k - 1)(b + c) \]

\[a - c = (k - 1)(b + c) \]

这意味着什么？

• slow从相遇点出发，再走c步，就到入口；
• head从头节点出发，再走c步，也会到入口。

3.2 代码实现

3.2.1 计算环长

点击查看代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head, * slow = head;
        while (fast != nullptr && fast->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow) { // 有环
                int cnt = 1; // 环中的节点数
                while (slow->next != fast) { 
                    slow = slow->next;
                    cnt += 1;
                }
                fast = head, slow = head;
                while (cnt > 0) {
                    fast = fast->next;
                    cnt -= 1;
                }
                while (slow != fast) {
                    slow = slow->next;
                    fast = fast->next;
                }
                return slow;
            }
        }
        return nullptr;
    }
};

3.2.2 不用计算环长

点击查看代码

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head, * slow = head;
        while (fast != nullptr && fast->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow) { // 有环
               fast = head;
               while (fast != slow) {
                    fast = fast->next;
                    slow = slow->next;
               }
               return slow;
            }
        }
        return nullptr;
    }
};

• 时间复杂度：$$O(n)$$
• 空间复杂度：$$O(1)$$

4 重排链表

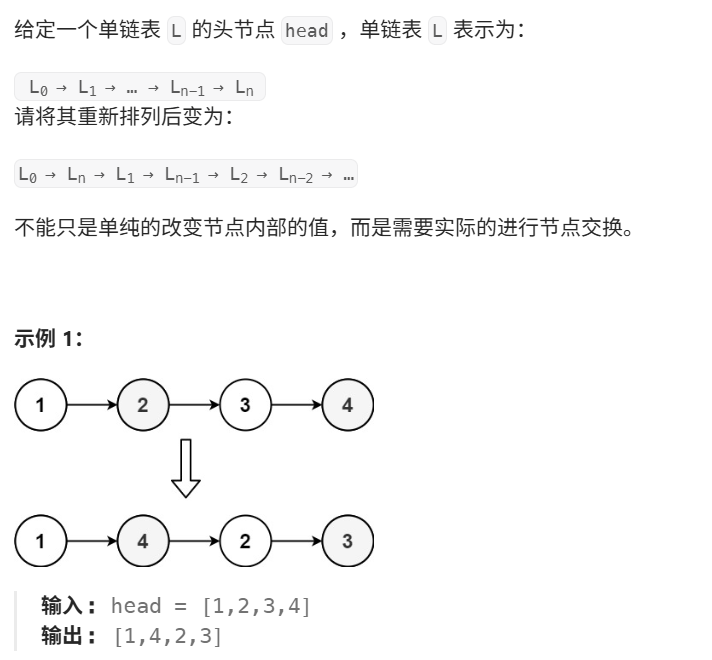
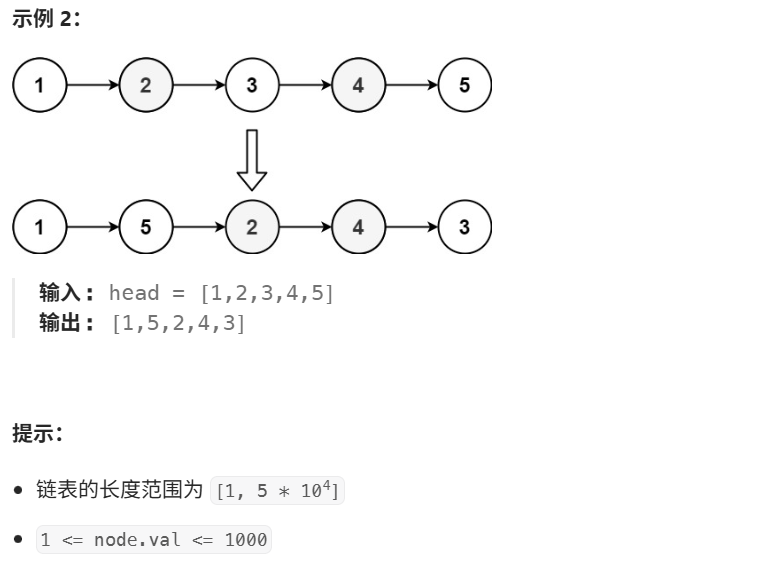
4.1 代码实现

点击查看代码

class Solution {
public:
    void reorderList(ListNode* head) {
        // 1. 找到中间节点1 - 2 -> 3(mid) -> 4 -> 5
        ListNode* mid = middleNode(head);
        // 2. 将中间节点及其往后的链表反转 1 -> 2 -> 3 <- 4 <- 5
        ListNode* head2 = reverseList(mid);
        ListNode* p = head, * q = head2;
        while (q != nullptr && q->next != nullptr) {
            ListNode* p_next = p->next;
            ListNode* q_next = q->next;
            q->next = p->next;
            p->next = q;
            p = p_next;
            q = q_next;
        }
    }
private:
    ListNode* middleNode(ListNode* head) {
        ListNode* slow = head, * fast = head;
        while (fast != nullptr && fast->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
        }
        return slow;
    }
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = nullptr;
        ListNode* cur = head;
        while (cur != nullptr) {
            ListNode* nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }
};

- 时间复杂度：$$O(n)$$ - 空间复杂度：$$O(1)$$