02 相向双指针

03 乘最多水的容器

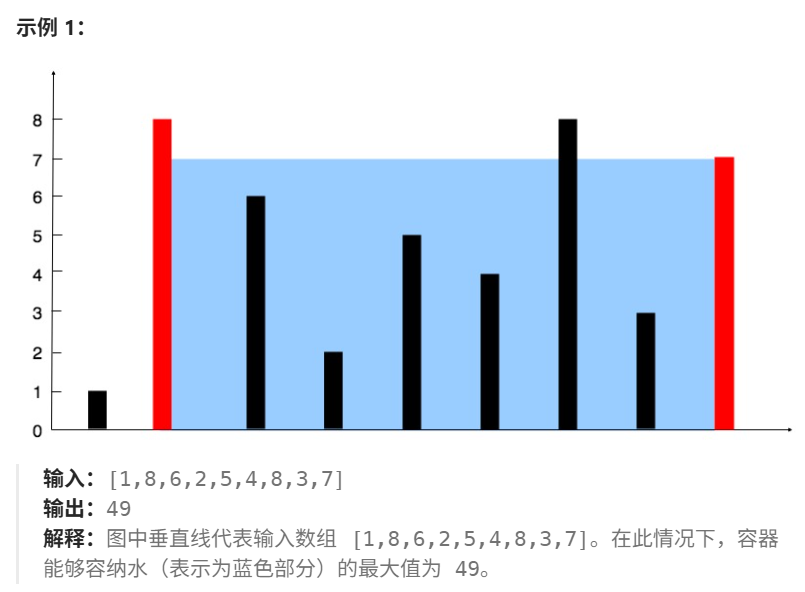
3.1 思考

考虑这条短的红线，它和中间的线构成容器，分类讨论

• 如果中间的线比它短，宽度减少，高度减少
• 如果中间的线比它长，宽度减少，高度不变
  因此，中间的任何一条线和它构成新的容器，都无法容纳更多的水。
  所以要想容纳更多的水，就需要移动短的这条线。

3.2 实现

点击查看代码

class Solution {
public:
    int maxArea(vector<int>& height) {
        int n = height.size();
        int left = 0, right = n - 1;
        int ans = 0;
        while (left < right) {
            int h = min(height[left], height[right]);
            ans = max(ans, (right - left) * h);
            if (height[left] < height[right]) {
                ++left;
            } else {
                --right;
            }
        }
        return ans;
    }
};

- 时间复杂度：$$O(n)$$ - 空间复杂度：$$O(1)$$

04 接雨水

4.1 思考

假设对于每个位置都有1个宽度为1的桶，那这个桶能接多少水，就取决于左右两边木板的高度。
对于一个桶而言，它左边木板的高度，取决于左边柱子的最大高度。

4.2 两种做法

4.2.1 计算前后缀

需要用到两个额外的数组。
对于第i个桶，一个数组记录0~i的柱子的最大高度（前缀的最大值），一个数组记录i~n-1的柱子的最大高度（后缀的最大值）。

这里可能有点疑惑，为什么针对前后缀，还要和i比较呢？
我们可以理解为对于第i个桶而言，第i个位置放置的石块height[i]就是在这个桶两边的木板高度。

举个例子，假如height[i]=3，这是前后缀的最大值。那么这个桶理论上可以装3个单位的水，但是结果现在这个桶装了3块石头，所以可容纳的水为0。

点击查看代码

class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size();
        vector<int> suf_max(n); // 后缀最大值
        // 对于第i个木桶，它的后缀最大值为[i, n - 1]
        suf_max[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; --i) {
            suf_max[i] = max(height[i], suf_max[i + 1]);
        }
        int ans = 0, pre_max = height[0];
        for (int i = 1; i < n; ++i) {
            pre_max = max(pre_max, height[i]); // 更新前缀最大值
            ans += min(suf_max[i], pre_max) - height[i];
        }
        return ans; 
    }
};

• 时间复杂度：$$O(n)$$
• 空间复杂度：$$O(n)$$

其实，我本来也不太理解为什么前后缀还要包含第i个位置呢？但是现在我发现其实不包含第i个位置也能做，

点击查看代码

class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size();
        vector<int> suf_max(n, 0); // 后缀最大值
        // 对于第i个木桶，它的后缀最大值为[i + 1, n - 1]
        suf_max[n - 1] = 0; // 不可能接到水
        for (int i = n - 2; i >= 0; --i) {
            suf_max[i] = max(height[i + 1], suf_max[i + 1]);
        }
        int ans = 0, pre_max = 0;
        for (int i = 1; i < n; ++i) {
            pre_max = max(pre_max, height[i - 1]);
            int h = min(suf_max[i], pre_max);
            ans += (h - height[i] < 0) ? 0: h - height[i];   
        }
        return ans; 
    }
};

4.2.2 相向双指针

一个木桶能接多少水，和它左右两边的木板高度（前缀最大值和后缀最大值）有关。
注意：前缀最大值（顺序遍历）和后缀最大值（倒序遍历）是不会变小的。
那么，假如我们顺序遍历，已经知道了当前木桶的前缀最大值，后缀最大值虽然不知道，但是可以用一个指针指向最后一个元素的后缀最大值，假如是1。分类讨论：

• 前缀最大值 < 后缀最大值，能接多少水取决于前缀最大值；
• 同理，如果后缀最大值 < 前缀最大值，那么能接多少水取决于后缀最大值。
  终于悟了。

点击查看代码

class Solution {
public:
    int trap(vector<int>& height) {
        // 相向双指针
        int n = height.size();
        int left = 0, right = n - 1;
        int ans = 0, pre_max = 0, suf_max = 0;
        while (left < right) {
            pre_max = max(pre_max, height[left]);
            suf_max = max(suf_max, height[right]);
            if (pre_max < suf_max) {
                ans += pre_max - height[left];
                ++left;  
            } else {
                ans += suf_max - height[right];
                --right;
            }
        }
        return ans;
    }
};

- 时间复杂度：$$O(n)$$ - 空间复杂度：$$O(1)$$