基和秩的物理解释

 

 

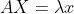
矩阵A实际可以看作一个变换，方程左边就是把向量x变到另一个位置而已；右边是把向量x作了一个拉伸，拉伸量是lambda。那么它的意义就很明显了，表达了矩阵A的一个特性就是这个矩阵可以把向量x拉长（或缩短）lambda倍，仅此而已。

任意给定一个矩阵A，并不是对所有的向量x它都能拉长（缩短）。凡是能被矩阵A拉长（缩短）的向量就称为矩阵A的特征向量（Eigenvector）；拉长（缩短）的量就是这个特征向量对应的特征值（Eigenvalue）。

值得注意的是，我们说的特征向量是一类向量，因为任意一个特征向量随便乘以一个标量结果肯定也满足上述方程，当然这两个向量都可以看成是同一特征向量，并且它们也对应于同一个特征值。

如果特征值是负数，则说明矩阵不但把特征向量拉长（缩短）了，而且使该向量的方向发生了反转（指向了相反的方向）。一个矩阵可能可以拉长（缩短）多个向量，因此它就可能有多个特征值。另外，对于实对称矩阵来说，不同特征值对应的特征向量必定正交。

我们也可以说，一个变换矩阵的所有特征向量组成了这个变换矩阵的一组基。所谓基，可以理解为坐标系的轴。我们平常用到的大多是直角坐标系，在线性代数中可以把这个坐标系扭曲、拉伸、旋转，称为基变换。我们可以按需求去设定基，但是基的轴之间必须是线性无关的，也就是保证坐标系的不同轴不要指向同一个方向或可以被别的轴组合而成，否则的话原来的空间就“撑”不起来了。在主成分分析（PCA）中，我们通过在拉伸最大的方向设置基，忽略一些小的量，可以极大的压缩数据而减小失真。

变换矩阵的所有特征向量作为空间的基之所以重要，是因为在这些方向上变换矩阵可以拉伸向量而不必扭曲和选择它，使得计算大为简单。因此特征值固然重要，但我们的终极目标却是特征向量。

 

 

证明：V（核所在的空间定义为V空间）的维度一定等于它的任意一个变换矩阵的核的维度加上值域的维度。

俗说：V的维度也就是V的基的数目。这些基分为两部分，一部分在核中，一部分是值域中非零象的原象（核和值域都是独立的子空间）。如果把V中的任意向量用基的形式写出来，那么这个向量必然也是一部分在核中，另一部分在值域中非零象的原象里。现在对这个向量作变换，核的那部分当然为零了（变换中核与行向量乘积为0，AX=0），另一部分的维度刚好等于值域的维度（b）。

 

可逆矩阵就是非奇异矩阵，非奇异矩阵也是可逆矩阵。 如果A为奇异矩阵，则AX=0有无穷解，AX=b有无穷解或者无解。如果A为非奇异矩阵，则AX=0有且只有唯一零解，AX=b有唯一解。

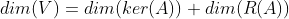
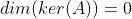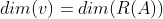俗说：A非奇异矩阵-可逆矩阵，AX=0有且只有唯一零解，，，秩就是基（轴线性无关）的维度--伴随矩阵，AX=b有唯一解（X是特征向量，唯一的基或者伴随矩阵变换下的基）。

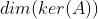           A奇异矩阵，AX=0有无穷解，AX=b有无穷解或者无解，不为0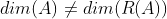，，非满秩，其X构成的向量组线性相关，需要降维得出特征向量组（PCA）。

 

 

注：知识点来自网络博主，只为学习和笔记记录，如有版权问题及时反馈，删博，谢谢。