柯西中值定理

To Start

其实我们可以将柯西中值定理理解成前面罗尔定理、拉格朗日中值定理的拓展。
拉格朗日中值定理就是罗尔定理的倾斜版，而柯西中值定理就是拉格朗日中值定理的拓展。说了和没说一样但是又确实如此。。具体如下。

描述

设f(x),g(x)在闭区间[a,b]上连续，在开区间（a，b）上可导，且\(g'（x）\neq 0\)，则至少存在一点\(\xi \epsilon (a,b)\)，使得\(\frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f'(\xi)}{g'(\xi)}\)

咋一看和拉格朗日中值定理也挺像的。就是把x换成了g（x）。这里只是打个比方，大家自行意会。这样做的效果就是：

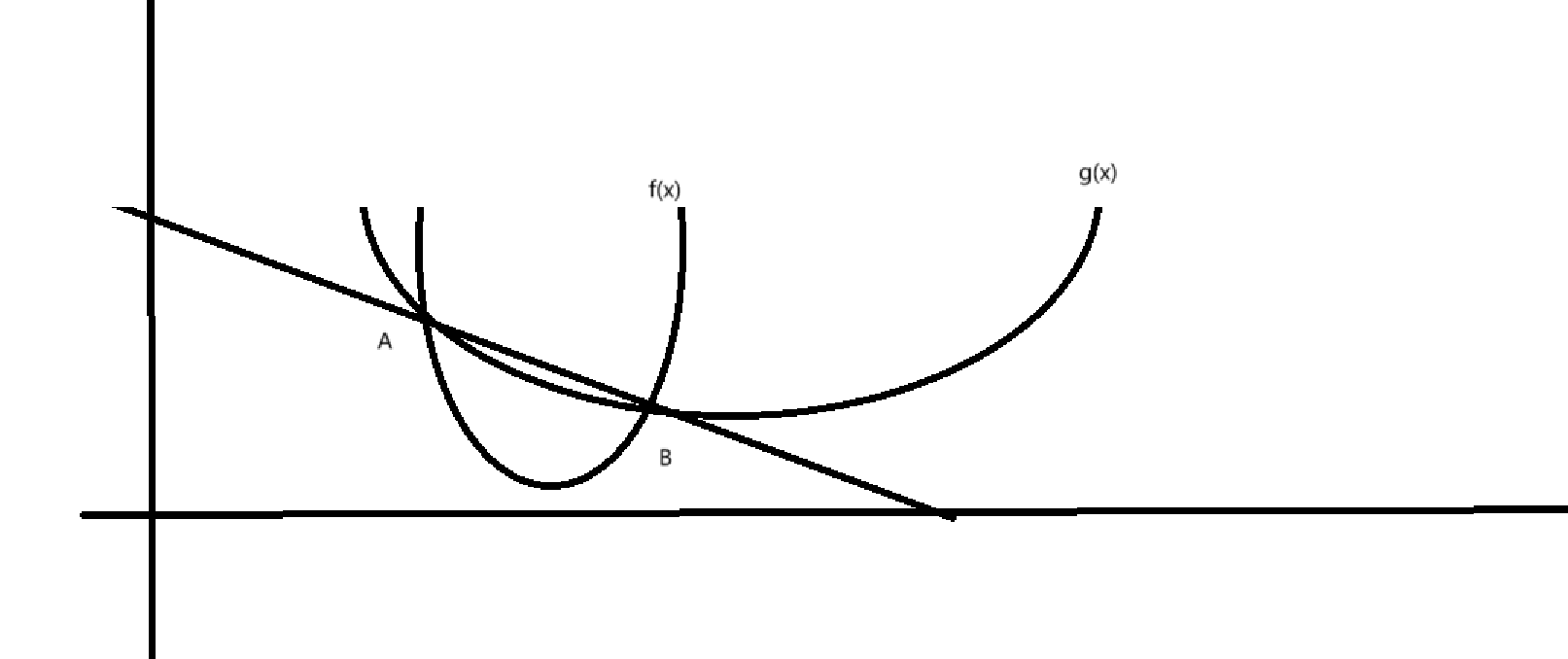
大概的意思就是说呢，区间（a，b）上f（x）必然会找到一个点的切线斜率于g（x）相等。
而且，如果当g（x）= x，那么这个结论会退化为拉格朗日中值定理；如果当g'（x）= 0，那么这个结论将会退化为罗尔定理。当然，我们不能把g'（x）放在分母的位置。有些地方会说f'（x）和g'(x)不同时为0，我想这样子的话是因为这两个就会是两个重合或平行的函数，没有讨论的意义，所以这样规定。