111
不同时期课件的坍缩式拼接,不建议观看。
线性基
一 .定义
线性基是针对某个序列生成的一个集合,它具有以下两条性质:
- 线性基中任意选择一些数的异或值所构成的集合,等于原序列中任意选择一些数的异或值所构成的集合。
- 线性基是满足上述条件的最小集合。
有了上面这两条性质,我们便可以得出如下几条推论:
- 原序列中任何数,都可以由线性基中一些数异或起来得到(由性质1直接得出)
- 线性基中不存在一组数,使得它们的异或值为 \(0\)(如果存在 \(x\oplus y\oplus z=0\),它就等价于 \(x\oplus y=z\) ,就可以删掉 \(z\) 使得异或集合不变,违背了性质2)
- 线性基中不存在两组取值集合,使得它们的异或和相等(不然你把这两个集合异或在一起就会得到异或和为 \(0\) 的集合)
二. 构造
我们采取动态构造的方法。
异或线性基中,我们记 \(b_i\) 表示线性基二进制第 \(i\) 位的数。
假设我们已经有了 \(n-1\) 个数的线性基,这时我们试图把第 \(n\) 个数 \(x\) 插入到线性基中。
void ins(LL x)
{
for (int i = 63;~i;i--)
{
if ((x>>i)&1)
{
if (!b[i]) return (void)(b[i] = x);
x ^= b[i];
}
}
}
我们要 尽量把 \(x\) 异或到 \(0\),因为一旦异或到 \(0\) 就表明 \(x\) 可以被线性基表示出来,就不用加入线性基了。
如果 \(x\) 的第 \(i\) 位是 \(0\),你要这时候异或上去了 \(b_i\),它的第 \(i\) 位就是 \(1\) 了,这个 \(1\) 以后消不掉(\(i\) 是 \(b_i\) 的最高位),故直接跳掉。
如果 \(x\) 的第 \(i\) 位是 \(1\),这时候必须异或上 \(b_i\) 才能消掉这一位(以后消不掉),不管对之后位数的影响。
那如果这时的 \(b_i\) 不存在呢?很显然这时 \(x\) 不能被线性基中的数表示出来,因此要把 \(x\) 加入线性基。
那什么时候这个 \(x\) 不会被加入线性基呢?很显然,当某次异或之后,\(x\) 变成了 \(0\)。则此时 \(x\) 可以被集合中数表示出来,可以不加入。
这就是构建线性基的方式,时间复杂度 \(O(n\log V)\)。
三.线性基操作
1.求最大异或和
LL ans = 0;
for (int i = 63;~i;i--) ans = max(ans,ans^b[i]);
从高位往低位枚举 \(b_i\),维护一个答案 \(ans\)。如果 \(ans\) 异或上 \(b_i\) 更优,则异或。
显然,如果 \(ans\) 的第 \(i\) 位是 \(1\),这时肯定不会异或,不然就把这个 \(1\) 给消去了,而就算之后的位上全是 \(1\),也是更劣的(其实就是按位贪心)。
而如果这位上是 \(0\),则一定要异或上 \(b_i\) 将这位变成 \(1\)。
因此最终呈现出来的结果就是异或之后答案更优就异或。
2.线性基合并
因为我们线性基是动态构造的,所以合并比较朴素,直接把其中一个线性基的数全都暴力插入到另一个线性基里就完成了。
简化题意:查询区间最大异或和。
简化题意:\(n\) 个线性基,单点插入,查询区间最大异或和。
简化题意:查询树上路径的最大异或和。
P11620 [Ynoi Easy Round 2025] TEST_34
简化题意:区间异或,查询区间最大异或和。
3.线性基上排序与贪心
简化题意:给定 \(n\) 个二元组 \((x_i,y_i)\),选出其中若干元素,选出的集合满足任意一个子集 \(x\) 异或起来不为 \(0\),问 \(\sum y_i\) 的最大值。
不能有任何一个子集异或出来为 0,可以转换为不存在任意一个数可以被集合中其他的数异或出来,其实就是线性基。
在满足线性基的性质上要求 \(\sum y_i\) 最大,由于线性基对插入的顺序没有要求,所以我们只需要把所有矿石按 \(y_i\) 从大到小排序之后进行插入就好了。
另一个做法是不排序,插入时若线性基这一位的值的 \(y\) 小于当前插入的 \(y\),将当前的二元组和线性基中的二元组交换一下,接着向后插入。
void ins(int j)
{
for (int i = 62;~i && c[j].a;i--)
{
if((c[j].a>>i)&1)
{
if(!b[i]) return (void)(b[i] = j);
if (c[j].b > c[b[i]].b) swap(j,b[i]);
c[j].a ^= c[b[i]].a;
}
}
}
回忆起NIM游戏先手必胜当且仅当所有石子堆的异或和不为 0。
我们可以发现,这题先手必然必胜——因为先手第一次总是可以取到只剩一堆石子,然后后手第一次就什么也取不了,然后先手第二次就可以直接取掉剩下那一堆。
从上面那个思路中,我们发现先手的目标肯定是去掉一些数,使得剩下的数不存在异或和为0的非空子集。不然,对手肯定就直接把除了那个非空子集外其它东西全部取光,先手就必败了。
不存在异或和为 \(0\) 的非空子集,这好像意味着序列中所有数都可以被插入一个线性基!
同样从大到小排序后插入。
4.每个异或值出现了多少次
根据线性基的性质:线性基中不存在两组取值集合,使得它们的异或和相等(不然你把这两个集合异或在一起就会得到异或和为 \(0\) 的几何)
构建线性基之后,记 \(len\) 为线性基大小,答案就是 \(2^{len}\)。
如果去重,可以直接从大到小扫一遍求出询问数的排名,不去重每个数重复次数为 \(2^{n-siz}\)。
CF959F Mahmoud and Ehab and yet another xor task
把询问离线下来。
分解质因数之后等价于所有质因数的次数都为偶数,等价于异或和为 \(0\) 。
四.线性基在图论方面的应用
dfs 找出所有的环,把对应的异或和扔进线性基中,最后查询最大异或和。
同上。
五.例题
End
由于会的比较少,所以线性基有很多东西没讲,大家可以根据下方博客自行学习。
第 k 小问题
一.静态全局第 k 小
单次询问使用 nth_element(a+1,a+k+1,a+n+1) 。
多次询问排一遍序。
二.动态全局第 k 小
平衡树,值域线段树上二分。
三.静态区间第 k 小
主席树上二分,整体二分
四.动态区间第 k 小
强制在线使用树套树:树状数组套值域线段树,树状数组套 01trie,树状数组套 vector
离线可以使用:整体二分
这里讲一下整体二分。
将修改拆分成先减后加,之后进行整体二分。
void solve(int l,int r,int L,int R)
{
if (l == r)
{
for (int i = L;i <= R;i++)
if (q[i].op) ans[q[i].id] = l;
return ;
}
int lc = L,rc = R,mid = (l+r)>>1;
for (int i = L;i <= R;i++)
{
if (q[i].op)
{
int k = Q(q[i].r)-Q(q[i].l-1);
if (q[i].k <= k) tmp[lc++] = q[i];
else q[i].k -= k,tmp[rc--] = q[i];
}
else
{
if (q[i].r <= mid)
A(q[i].l,q[i].k),tmp[lc++] = q[i];
else tmp[rc--] = q[i];
}
}
for (int i = L;i <= R;i++)
if (!q[i].op && q[i].r <= mid) A(q[i].l,-q[i].k);
reverse(tmp+rc+1,tmp+R+1);
for (int i = L;i <= R;i++) q[i] = tmp[i];
solve(mid+1,r,rc+1,R),solve(l,mid,L,lc-1);
}
五.第 k 小数对和
将两个数列从小到大排序后,两两形成数对的和如下图。
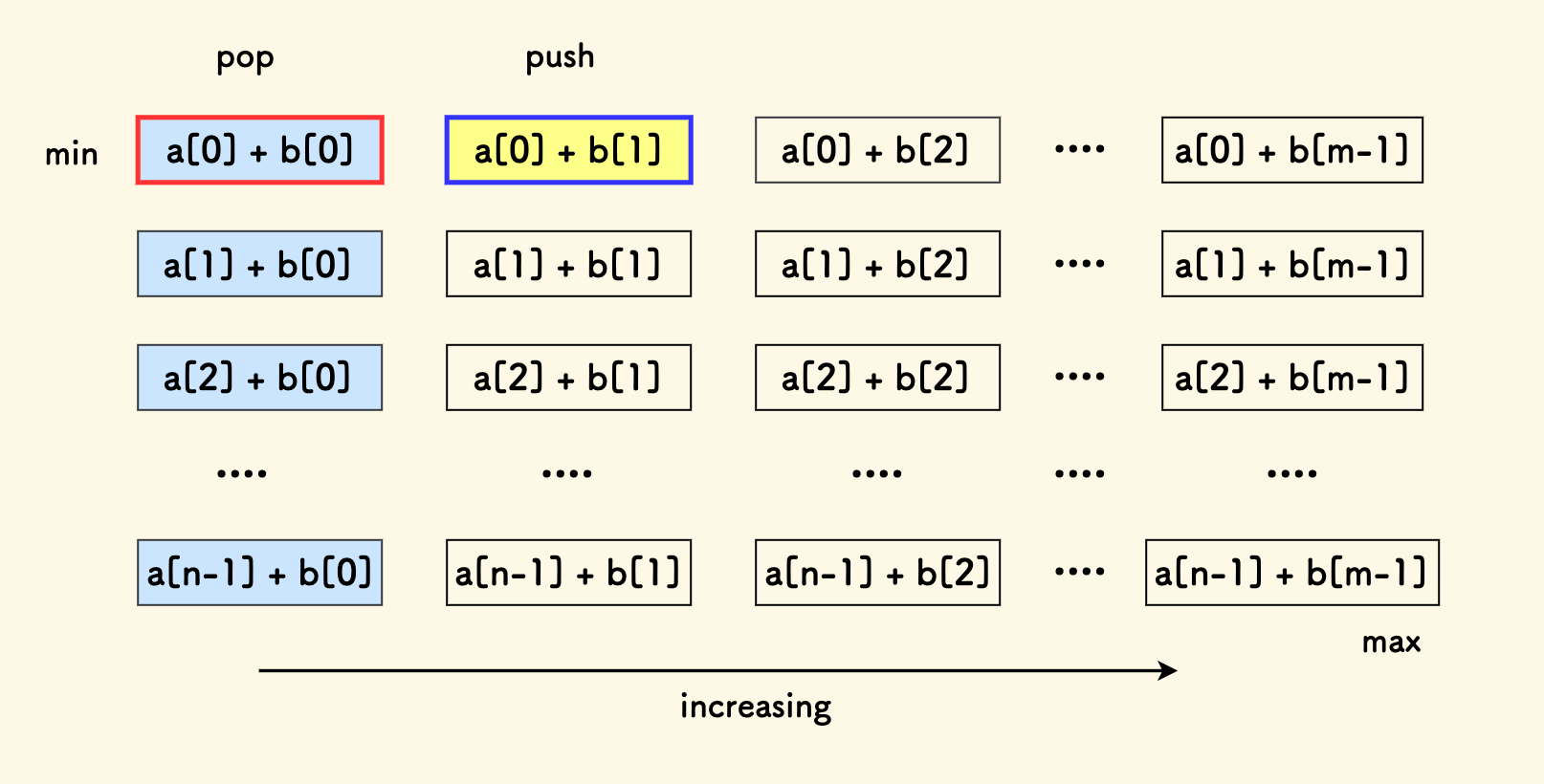
维护一个优先队列,初始将每一行的第一个数放进去,每次去除队首同时将对应行下一个数放入优先队列,时间复杂度 \(O(k\log n)\)。
六.第 \(k\) 小子段和
区间和等于前缀和数组的差,及前缀和数组为 \(a_i\)。
对于每个位置,我们把 \(-a_{l-1}+\max\limits_{i=l+L-1}^{l+R-1}a_i\) 放入优先队列,每次取出队首同时使用 ST 表查询两侧区间的最大值放入优先队列。
杂项
树上邻点第 k 小,对于每个点维护一个值域线段树或者平衡树,把儿子插入进去。
树链第 k 小,树剖把树链剖成 \(\log n\) 段,然后值域线段树上进行多树二分。
子树第 k 小,静态可以线段树合并或者平衡树启发式合并,带修的话,拍成 \(dfn\) 序列,就变成了动态区间第 \(k\) 小。
数据结构再入门
前言
至于为什么备课备的这么慢,其实是准备了一些小题,因为我个人认为只把板子讲会了似乎对做题确实是没什么用处,大家可以思考一下自己听完多项式之后现在会不会写多项式题(虽然不太恰当,因为大家多项式之前确实是没涉及过)。
主要还是数据结构在你会写的同时还要学好多好多 trick 才能做题,同时大家平时对数据结构的练习和了解相较于其他算多的了,所以感觉只讲板子意一是大家学不到什么东西,二是比较敷衍,不是很负责。
因此这次课有些是对 kinna 上次讲的线段树和平衡树所涉及的一些 trick 的补充。
小验收?
题意:给你一个长为 \(n\) 的序列 \(a\)
每次两个操作:
-
修改 \(x\) 位置的值为 \(y\)
-
查询区间 \([l,r]\) 是否可以重排为值域上连续的一段
对于 \(100\%\) 的数据,\(n,m \le 500000\)
初始值的值域小于 \(2.5\times 10^7\),修改操作的 \(y\) 小于等于 \(n\)。
Sol:首先析合树不支持修改,所以放弃你幼稚的想法,考虑正解。
- 一个序列能重排为值域上连续的一段,那么 \(\max-\min = r-l\) 。假如这里是排列的话,显然维护一下区间 max 和 min 就足够了,可惜不是。
- 考虑额外维护区间和。
- 多维护一个区间平方和,若平方和相等,那么大概率就是了。(随机数据下维护了平方和正确率已经非常高了,同时也就是说能构造数据卡掉,但是谁会卡这个呢?)
来个经验
P5278 算术天才⑨与等差数列
题意:一个长度为 \(n\) 的序列,其中第 \(i\) 个数为 \(a_i\)。
每次询问 \(l,r,k\),问区间 \([l,r]\) 内的数从小到大排序后能否形成公差为 \(k\) 的等差数列。
注意:只有一个数的数列也是等差数列。
对于 \(100\%\) 的数据, \(1\le n,m \le 3\times 10^5\),\(0\le a_i,y,k \le 10^9\)。
Sol:与上题类似。
- \(\max-\min = (r-l)*k\)
- \(sum1 = (\max+\min)*(r-l+1)/2\)
- \(sum2 = \min^2*(r-l+1)+(r-l+1)*(r-l)*\min+(1^2+2^2+3^2+...)*k^2\)
一、可持久化数据结构
1. 可持久化数组 & 可持久化线段树
引入:P3919 【模板】可持久化线段树 1(可持久化数组)
题意:如题,你需要维护这样的一个长度为 $ N $ 的数组,支持如下几种操作
-
在某个历史版本上修改某一个位置上的值
-
访问某个历史版本上的某一位置的值
此外,每进行一次操作(对于操作2,即为生成一个完全一样的版本,不作任何改动),就会生成一个新的版本。版本编号即为当前操作的编号(从1开始编号,版本0表示初始状态数组)
对于100%的数据:$ 1 \leq N, M \leq {10}^6, 1 \leq {loc}_i \leq N, 0 \leq v_i < i, -{10}^9 \leq a_i, {value}_i \leq {10}^9$
Sol:一个非常 naive 的想法是每次把整个数组复制一遍,时空复杂度双双暴毙。
想偷懒使用 vector?显然错误的想法。
考虑把他建成一棵线段树,每次单点修改或查询时时把经过的节点复制一遍,时间空间复杂度均为 \(O(n\log n)\) 。
这里运用的思想就是最大程度利用历史版本的信息,当我们不得不对树的一些结构或信息进行修改时再新开节点修改,这样不会影响历史版本的信息。
想要图片?
void M(int l,int r,int pos,int k,int &i)
{
int p = i;i = ++cnt;tr[i] = tr[p];
if (l == r) {tr[i].v = k;return ;}
int mid = (l+r)>>1;
if (pos <= mid) M(l,mid,pos,k,tr[i].ls);
else M(mid+1,r,pos,k,tr[i].rs);
}
题意:
给定 \(n\) 个集合,第 \(i\) 个集合内初始状态下只有一个数,为 \(i\)。
有 \(m\) 次操作。操作分为 \(3\) 种:
-
1 a b合并 \(a,b\) 所在集合; -
2 k回到第 \(k\) 次操作(执行三种操作中的任意一种都记为一次操作)之后的状态; -
3 a b询问 \(a,b\) 是否属于同一集合,如果是则输出 \(1\),否则输出 \(0\)。
对于 \(100\%\) 的数据,\(1\le n\le 10^5\),\(1\le m\le 2\times 10^5\),\(1 \le a, b \le n\)。
Sol:并查集如何可持久化?容易发现一次合并操作其实就是 fa 数组和 siz 数组的修改,把这两个数组可持久化即可。
题意:给定 \(n\) 个整数构成的序列 \(a\),将对于指定的闭区间 \([l, r]\) 查询其区间内的第 \(k\) 小值。
- 对于 \(100\%\) 的数据,满足 \(1 \leq n,m \leq 2\times 10^5\),\(0\le a_i \leq 10^9\),\(1 \leq l \leq r \leq n\),\(1 \leq k \leq r - l + 1\)。
Sol: 我们有一个空的权值线段树,每次把询问的区间取出来,一个一个数插进去是不是就可以在线段树上二分了?是的。
那么我们把他可持久化之后,对于一次查询区间 \([l,r]\) ,用 r 版本的信息减去 l-1 版本的信息剩下的权值线段树是不是就是 \([l,r]\) 里的数一个一个插进去所得到的权值线段树?然后就没了。
权值线段树的话记得离散化,就算是动态开点也要离散化(有的时候卡有的时候不卡而已)。
不会线段树二分?
int Q(int a,int b,int l,int r,int k)
{
if (l == r) return l;
int siz = tr[tr[b].ls].cnt-tr[tr[a].ls].cnt;
int mid = (l+r)>>1;
if (siz >= k) return Q(tr[a].ls,tr[b].ls,l,mid,k);
else return Q(tr[a].rs,tr[b].rs,mid+1,r,k-siz);
}
题意:
给一个长度为 \(n\) 的正整数序列 \(a\)。共有 \(m\) 组询问,每次询问一个区间 \([l,r]\) ,是否存在一个数在 \([l,r]\) 中出现的次数严格大于一半。如果存在,输出这个数,否则输出 \(0\)。
\(1 \leq n,m \leq 5 \times 10^5\),\(1 \leq a_i \leq n\)。
Sol: 发现是静态区间查询,那么可以用可持久化线段树。
但是该怎么找到区间内是否存在一个数出现次数超过一半呢?
同样是线段树上二分,哪个儿子记录的 \(cnt > len/2\) 就往哪边走,假如能走到叶子结点就代表找到了这个数。
经验们:
P7261 [COCI2009-2010#3] PATULJCI
PATULJCI - Snow White and the N dwarfs
再来个题:
题意:
给出一个 \(1\) 到 \(n\) 的排列,现在对这个排列序列进行 \(m\) 次局部排序,排序分为两种:
0 l r表示将区间 \([l,r]\) 的数字升序排序1 l r表示将区间 \([l,r]\) 的数字降序排序
注意,这里是对下标在区间 \([l,r]\) 内的数排序。
最后询问第 \(q\) 位置上的数字。
对于 \(100\%\) 的数据,\(n,m\leq 10^5\),\(1\leq q\leq n\)
Sol: 正常做的话肯定是不好做,但是欣喜地发现只有一个询问???
首先对于一个数 x ,我们把大于等于它的数设为 1 ,否则设为 0 ,那么进行 m 次排序后,若第 q 位为 1 ,是不是就代表着这 m 次排序过后第 q 位的数要大于 x ?然后容易发现这是不是满足单调性来着?好像是能二分答案的吧。
那么怎么处理排序?你都转化为 01 串了,直接拿线段树维护一下不就好了?
题意:一个长度为 \(n\) 的序列 \(a\),设其排过序之后为 \(b\),其中位数定义为 \(b_{n/2}\),其中 \(a,b\) 从 \(0\) 开始标号,除法下取整。
给你一个长度为 \(n\) 的序列 \(s\)。
回答 \(Q\) 个这样的询问:\(s\) 的左端点在 \([a,b]\) 之间,右端点在 \([c,d]\) 之间的子区间中,最大的中位数。
其中 \(a<b<c<d\)。
位置也从 \(0\) 开始标号。
我会使用一些方式强制你在线。
对于 \(100\%\) 的数据,\(1\leq n \leq 20000\),\(1\leq Q \leq 25000\),\(1\leq a_i\leq 10 ^ 9\)。
Sol:跟上道题同样的 trick ,我们二分答案这个中位数。
但是还是有些不一样的,对于一个数 x ,我们把小于它的设为 -1 ,大于等于它的设为 1 ,那么对于一个区间,如果它的和大于等于 0 ,那么是不是代表这个区间的中位数大于等于 x ?
那么对于当前二分的数 x ,我们贪心的想肯定是让区间和尽可能的大这样更容易满足和大于等于零进而二分出更大的中位数,那我我们是不是就是要求左端点在 \([a,b]\) 之间 ,右端点在 \([c,d]\) 之间的最大子段和?猜你想找 GSS5 - Can you answer these queries V。(这里批评 kinna 线段树讲的 trick 太少还得让我来补)
但是还有问题,现在会二分了,也会求最大子段和了,那么对于每次二分的数 x ,总不能每次都建一遍线段树吧?这时候终于扣上题了,我们把输入的序列从小到大排好序,从左往右遍历一个一个把数的值设为 -1 ,同时保留历史版本,这不就是我们的可持久化线段树吗!!!
然后就没了,综合题,难评。
2.可持久化01trie
对于可持久化01trie在维护数值方面是全方位薄杀和持久化平衡树的,同时,它还能处理平衡树所不能处理的异或,所以不要再写维护数值的可持久化平衡树了!!!
What is 01trie?
只有 0 和 1 两个儿子的 trie 树,插入一个数时按二进制插入,他能干什么?
首先,它支持插入和删除,求前驱后继,区间第 k 小,一个数的排名。。。
那么对他可持久化之后能干什么?
先来个只有他能干的。
题意:
给定一个非负整数序列 \(\{a\}\),初始长度为 \(N\)。
有 \(M\) 个操作,有以下两种操作类型:
A x:添加操作,表示在序列末尾添加一个数 \(x\),序列的长度 \(N\) 加 \(1\)。Q l r x:询问操作,你需要找到一个位置 \(p\),满足 \(l \le p \le r\),使得:\(a[p] \oplus a[p+1] \oplus ... \oplus a[N] \oplus x\) 最大,输出最大值。
- 对于所有测试点,\(1\le N,M \le 3\times 10 ^ 5\),\(0\leq a_i\leq 10 ^ 7\)。
Sol:考虑维护前缀异或数组,那么对于每个询问就是找到一个位置 p 满足 \(l-1\le p\le r-1\),使得 \(a_p\oplus a_n\oplus x\) 最大,和可持久化线段树同样的,我们要利用 \([l-1,r-1]\) 的信息,只需要把第 r-1 个版本和第 l-2 个版本做差即可,做完差后正常 01trie 上二分。
题意:
给定一棵 \(n\) 个节点的树,每个点有一个权值。有 \(m\) 个询问,每次给你 \(u,v,k\),你需要回答 \(u \text{ xor last}\) 和 \(v\) 这两个节点间第 \(k\) 小的点权。
对于 \(100\%\) 的数据,\(1\le n,m \le 10^5\),点权在 \([1, 2 ^ {31} - 1]\) 之间。
Sol:
假如是序列的话大家都会做吧,序列搬到树上同理,变成树上前缀和就好了。
题意:
现在有一颗以 \(1\) 为根节点的由 \(n\) 个节点组成的树,节点从 \(1\) 至 \(n\) 编号。树上每个节点上都有一个权值 \(v_i\)。现在有 \(q\) 次操作,操作如下:
-
\(1~x~z\):查询节点 \(x\) 的子树中的节点权值与 \(z\) 异或结果的最大值。
-
\(2~x~y~z\):查询节点 \(x\) 到节点 \(y\) 的简单路径上的节点的权值与 \(z\) 异或结果最大值。
-
对于 \(100\%\) 的数据,保证 \(2\leq n, q \leq10^5\),\(1 \leq u, v, x, y \leq n\),\(1 \leq op \leq 2\),\(1 \leq v_i, z \lt 2^{30}\)。
Sol:对于两种询问发现一个是链一个是子树,导致我们如果按 dfn 序建树的话只能处理 1 询问,按树边建树的话只能处理 2 询问,所以建两棵树就好了。、
题意:
给定长度为 \(n\) 的数列 \(X={x_1,x_2,...,x_n}\) 和长度为 \(m\) 的数列 \(Y={y_1,y_2,...,y_m}\),令矩阵 \(A\) 中第 \(i\) 行第 \(j\) 列的值 \(A_{i,j}=x_i\ \operatorname{xor}\ y_j\),每次询问给定矩形区域 \(i∈[u,d],j∈[l,r]\),找出第 \(k\) 大的 \(A_{i,j}\)。
对于 \(100\%\) 的数据
- \(0\leq X_i,Y_j<2^{31}\),
- \(1\leq u\leq d\leq n\leq 1000\),
- \(1\leq l\leq r\leq m\leq 300000\),
- \(1\leq k\leq (d-u+1)\times (r-l+1)\), \(1\leq p\leq 500\)。
Sol:询问矩阵好像挺难的样子,能不能建一个可持久化01trie套可持久化01trie呢?不行的话每次把这个矩阵的数暴力拿出来排个序呢?难评。
容易发现 \(1\le n\le 1000\) 而且 \(\le p\le 500\) ,那么我们直接把 Y 数列建成一棵可持久化01trie,每次询问拿出来 d-u+1 个根一起二分行不行呢?复杂度 \(O(np\log m)\) 好像能跑过去。
问题又来了,怎么多树二分?
多树二分其实跟一棵树上二分一样,不过是把这 n 个根的贡献加起来和 k 比较。
感觉看代码会比较好
int Q(int dep,int ans,int k)
{
if(dep < 0) return ans;
int sum = 0;
for (int i = u;i <= d;i++)
{
bool f = (x[i]>>dep)&1;
sum += s[ch[b[i]][!f]]-s[ch[a[i]][!f]];
}
for (int i = u;i <= d;i++)
{
bool f = ((x[i]>>dep)&1)^(k <= sum);
a[i] = ch[a[i]][f],b[i] = ch[b[i]][f];
}
if(k <= sum) ans += (1<<dep);
else k -= sum;
return Q(dep-1,ans,k);
}
接下来撕票可持久化平衡树。
是不是要先写掉平衡树的板子来着
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
const int N = 1e5+5;
int n,m,a[N],cnt,ch[N<<5][2],siz[N<<5],rt;
void M(int dep,int p,int k,int &i)
{
if(!i) i = ++cnt;
if(dep < 0) return (void)(siz[i] += k);
if((p>>dep)&1) M(dep-1,p,k,ch[i][1]);
else M(dep-1,p,k,ch[i][0]);
siz[i] = siz[ch[i][0]]+siz[ch[i][1]];
}
int Q(int dep,int k,int s,int i)
{
if(dep < 0) return s;
int sum = 0;
if((k>>dep)&1) return Q(dep-1,k,s+siz[ch[i][0]],ch[i][1]);
else return Q(dep-1,k,s,ch[i][0]);
}
int Q1(int dep,int k,int s,int i)
{
if(dep < 0) return s;
if(siz[ch[i][0]] >= k) return Q1(dep-1,k,s,ch[i][0]);
else return Q1(dep-1,k-siz[ch[i][0]],s+(1<<dep),ch[i][1]);
}
int main()
{
int n;cin >> n;
while(n--)
{
int op,x;cin >> op >> x;
if(op == 1) M(28,x+1e7,1,rt);
if(op == 2) M(28,x+1e7,-1,rt);
if(op == 3) cout << Q(28,x+1e7,0,rt)+1 << '\n';
if(op == 4) cout << int(Q1(28,x,0,rt)-1e7) << '\n';
if(op == 5) cout << int(Q1(28,Q(28,x+1e7,0,rt),0,rt)-1e7) << '\n';
if(op == 6) cout << int(Q1(28,Q(28,x+1e7+1,0,rt)+1,0,rt)-1e7) << '\n';
}
return 0;
}
剩下的就是修改的时候复制一遍了。
3.可持久化平衡树
可持久化平衡树专指可持久化 fhq。
至于怎么可持久化,同样是修改的时候复制一下节点就好了。
什么时候会修改?当然是 split 和 merge 。
void copy(int x,int y)
{ls[x] = ls[y],rs[x] = rs[y],siz[x] = siz[y],v[x] = v[y],rd[x] = rd[y];}
void split(int i,int k,int &x,int &y)
{
if (!i) {x = y = 0;return ;}
copy(++cnt,i);i = cnt;
if (v[i] <= k) x = i,split(rs[i],k,rs[i],y),pushup(x);
else y = i,split(ls[i],k,x,ls[i]),pushup(y);
}
int merge(int x,int y)
{
if (!x || !y) return x|y;int rt = ++cnt;
if (rd[x] < rd[y]) {copy(rt,x);rs[rt] = merge(rs[rt],y),pushup(rt);return rt;}
else {copy(rt,y);ls[rt] = merge(x,ls[rt]),pushup(rt);return rt;}
}
所以可持久化就是无脑复制节点就行了。
来个题。
题意:有 \(n\) 种 T 恤,每种有价格 \(c_i\) 和品质 \(q_i\)。
有 \(m\) 个人要买 T 恤,第 \(i\) 个人有 \(v_i\) 元,每人每次都会买一件能买得起的 \(q_i\) 最大的 T 恤。一个人只能买一种 T 恤一件,所有人之间都是独立的。
问最后每个人买了多少件 T 恤?如果有多个 \(q_i\) 最大的 T 恤,会从价格低的开始买。
Sol:把 T 恤按优先级排遍序之后,从左往右扫,容易发现每次进行的操作就是将所有大于等于 \(c_i\) 的数整体加 1 并减去 \(c_i\) ,考虑数据结构维护。。。How? 然后发现好像没有数据结构能干这活,吗?平衡树为什么维护不了?
是不是因为,每次修改减去 \(c_i\) 会修改好多数的大小,假如要维护平衡树的性质就必须把所有数重新插入一遍,(数值平衡树维护区间修改不是找死。。。)
但是有不有一种可能,对于一次修改,我们只把那些减完之后会破坏平衡树性质的数拿出来重新插入一遍不就行了?先不考虑复杂度的话,那么究竟哪些数需要重新插入呢?
首先,\([0,c)\) 这些数不会被修改,\([c,2c)\) 这些数减完之后会变为 \([0,c)\) ,而 \([2c,+\infty]\) 会变为 \([c,+\infty]\)
那是不是只有 \([c,2c)\) 的数操作完后需要重新插入,所以每次修改把平衡树分裂为三部分 \([0,c),[c,2c),[2c,+\infty]\) 即可,对于 \([c,2c)\) 我们一个一个减完之后重新插入,对于 \([2c,+\infty]\) 打一个 lazytag 即可。
那么复杂度对不对呢?
考虑一个数被修改之后数值大小至少是变为原来的一半的,因此一个数只会被插入 \(\log\) 次, 最劣复杂度 \(O(n\log^2n)\)
但是我们讲的不是可持久化平衡树吗?
所以我们先给这题来个强制在线,那么该怎么办?
连一刻都没有为平衡树的死亡哀悼,立刻赶到战场的是可持久化平衡树。
\(Sol\):
先考虑一个简单的 dp(其实是橙色的递推) ,同样是先把 T 恤按优先级排好序。
设 \(f_{i, j}\) 为从第 \(i\) 件开始买,有 \(j\) 元钱,能买到的 T 恤数量,考虑如何转移。
$f_{i,j} = \begin{cases} f_{i+1,j} & j<c_i \f_{i+1,j}+1& j\ge c_i\end{cases} $
从后往前转移,因为前面的优先级比后面的高,所以肯定能买前面的先买前面的。
那么如何优化呢?
每次在前面增加衣服的时候相当于 \([0,C)\) 的区间完全不变,\([C,maxv)\) 的区间由 \([0,maxv-C)\) 的区间平移过来,并且区间加上1,这不就是区间复制吗,可持久化平衡树足矣。这样我们 dp 完后对于每次询问单点查询即可。
然后你就会发现这又何尝不是值域平衡树呢(至于为什么是值域因为你 dp 数组定义的就是啊)但是值域是 \([1,10^9]\) 欸,照常说平衡树是要先把 \([1,10^9]\) 这些点一个一个插入进去之后才能 split 和 merge,不然你平衡树要按 siz 分裂和合并的,也就代表初始你这颗树一定是被建好了的。但是这样复杂度又寄了啊,怎么办?
我们这可是可持久化平衡树,能最大程度利用先前版本的信息,高效处理区间复制,所以我们初始开一个节点,让他自我复制个 30 次它的 siz 不久超过 \(10^9\) 了吗?没听太懂?
可持久化平衡树,Amazing!
4.可持久化可并堆
可持久化不都一个套路吗,修改啥 copy 啥,同时鉴于可持久化可并堆除了写 k 短路没啥用了,所以摆了。
树套树
KDT主要解决二维平面上的矩形修改,矩形查询问题
树套树主要解决二维平面上的单点修改,矩形查询或者矩形修改单点查询问题
“CDQ分治”功能上和树套树是等价的,所以这里讲题的时候主要讲树套树做法,因为我们关注的是数据结构题的思维方法而不是具体实现细节
树套树就其实就是树的每个节点都维护一棵树。。。
1.树状数组套平衡树
题意:
-
查询 \(k\) 在区间内的排名
-
查询区间内排名为 \(k\) 的值
-
修改某一位置上的数值
-
查询 \(k\) 在区间内的前驱(前驱定义为严格小于 \(x\),且最大的数,若不存在输出
-2147483647) -
查询 \(k\) 在区间内的后继(后继定义为严格大于 \(x\),且最小的数,若不存在输出
2147483647)
\(1\le n,m\le5\times 10^4\),序列中的值在任何时刻 \(\in[0,10^8]\)。
Sol:
假如抛去区间限制,那么是不是就是平衡树板题了。
那么区间限制怎么办?每次把 \([l,r]\) 里面的数拿出来建一棵平衡树不就行了?但是这不就寄了吗,那怎么办?
考虑我们是怎么引入树状数组的
我们要在单点修改的同时维护 \([l,r]\) 的区间和,因此要用到树状数组,对吧?
此时树状数组维护的每个节点是不是 \([l,r]\) 的和。
那么我们让树状数组每个节点维护的是 \([l,r]\) 这些数所形成的平衡树呢?
如何实现呢?先看一棵树状数组。
每次修改的时候,我们是不是能找出 \(\log n\) 个被修改的节点,那么我们对这 \(\log n\) 棵平衡树都进行一次修改操作就可以了?
对于查询的话,我们同样能找出来 \(\log n\) 棵平衡树能拼成我们所求区间的平衡树
对于 3 操作:
单点修改拆成删除后插入。
//rt[i] 树状数组i节点的平衡树的根
void add(int i,int a,int b)
{
while(i <= n)
{
int x,y,z;split(rt[i],a,x,y);split(x,a-1,x,z);
rt[i] = merge(merge(x,merge(ls[z],rs[z])),y);
ins(i,b);
i += i&-i;
}
}
对于 1 操作:
用 \([1,r]\) 区间内小于 k 的数的个数减去 \([1,l-1]\) 内小于 k 的数的个数加 1 ,即为 k 在 \([l,r]\) 的排名
//Q() [l,r] 内小于 k 的数的个数
int Q(int l,int r,int k)
{
int sum = 0;
while(r) sum += rk(r,k),r -= r&-r;
while(l) sum -= rk(l,k),l -= l&-l;
return sum;
}
对于 2 操作:
不是,这 \(\log n\) 棵平衡树倒是能找出来,但是这平衡树也不好多树二分啊!
怎么办怎么办怎么办怎么办
只能二分了,二分出排名恰好为 k 的数值即可。
if(op == 2)
{
cin >> k;
int L = 0,R = 1e9;
while(L < R)
{
int mid = (L+R)>>1;
if(Q(l-1,r,mid) >= k) R = mid;
else L = mid+1;
}
cout << L << '\n';
}
没错复杂度 \(\log^3\) ,这就是内层套平衡树的劣根性,除了空间小之外,还拥有常数大,以及不可多树二分(其实可以,不过我不会)导致某些操作要比别的树多一个 \(\log\) 的优点。
前驱后继大家都会求吧,就是求排名和求排名为 k 这两个函数一起用而已。
但是,虽然空间复杂度十分优越,但是

虽然不知道为什么 WA 了,但是正常情况下 \(\log^3\) 的复杂度是肯定过不了的。
题意:
给定一个含有 \(n\) 个数的序列 \(a_1,a_2 \dots a_n\),需要支持两种操作:
Q l r k表示查询下标在区间 \([l,r]\) 中的第 \(k\) 小的数C x y表示将 \(a_x\) 改为 \(y\)
对于 \(100\%\) 的数据,\(1\le n,m \le 10^5\),\(1 \le l \le r \le n\),\(1 \le k \le r-l+1\),\(1\le x \le n\),\(0 \le a_i,y \le 10^9\)。
Sol:
上道题的弱化版,同样的

所以非必要内层不要套平衡树。
2.树状数组套01trie
所以我们迎来伟大的 01trie
对于 3 操作:同平衡树。
对于 1 操作:同平衡树。
对于 2 操作:
对于区间限制,我们拆成两个区间 \([1,r]\) 和 \([1,l-1]\)
对于这两个区间,各拆成 \(\log n\) 棵树,类比上面异或运算里讲的多树二分。
左儿子个数小于 k 就往右走,否则往左走。
对于4,5操作:同平衡树。
现在你已经能切掉它了。
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
const int N = 5e4+5;
int n,m,a[N],cnt,ch[N<<9][2],siz[N<<9],rt[N];
void add(int dep,int p,int k,int &i)
{
if(!i) i = ++cnt;
if(dep < 0) return (void)(siz[i] += k);
if((p>>dep)&1) add(dep-1,p,k,ch[i][1]);
else add(dep-1,p,k,ch[i][0]);
siz[i] = siz[ch[i][0]]+siz[ch[i][1]];
}
//修改
void M(int i,int a,int b)
{
while(i <= n)
{
if(~a) add(31,a,-1,rt[i]);
add(31,b,1,rt[i]);
i += i&-i;
}
}
vector < int > t1,t2;
int A(int dep,int k,int s)
{
if(dep < 0) return s;
int sum = 0;
for (int i : t1) sum += siz[ch[i][0]];
for (int i : t2) sum -= siz[ch[i][0]];
if(sum < k)
{
for (int i = 0;i < t1.size();i++) t1[i] = ch[t1[i]][1];
for (int i = 0;i < t2.size();i++) t2[i] = ch[t2[i]][1];
return A(dep-1,k-sum,s+(1<<dep));
}
else
{
for (int i = 0;i < t1.size();i++) t1[i] = ch[t1[i]][0];
for (int i = 0;i < t2.size();i++) t2[i] = ch[t2[i]][0];
return A(dep-1,k,s);
}
}
int Q2(int dep,int k,int s,int i)
{
if(dep < 0) return s;
int sum = 0;
if((k>>dep)&1) return Q2(dep-1,k,s+siz[ch[i][0]],ch[i][1]);
else return Q2(dep-1,k,s,ch[i][0]);
}
//排名
int Q1(int l,int r,int k)
{
int sum = 0;
while(r) sum += Q2(31,k,0,rt[r]),r -= r&-r;
while(l) sum -= Q2(31,k,0,rt[l]),l -= l&-l;
return sum;
}
//第 k 小
int Q(int l,int r,int k)
{
t1.clear(),t2.clear();
while(r) t1.pb(rt[r]),r -= r&-r;
while(l) t2.pb(rt[l]),l -= l&-l;
return A(31,k,0);
}
int main()
{
cin >> n >> m;
for (int i = 1;i <= n;i++)
cin >> a[i],M(i,-1,a[i]);
for (int i = 1;i <= m;i++)
{
int op,l,r,x;cin >> op >> l >> r;
if(op == 1) cin >> x,cout << Q1(l-1,r,x)+1 << '\n';
if(op == 2) cin >> x,cout << Q(l-1,r,x) << '\n';
if(op == 3) M(l,a[l],r),a[l] = r;
if(op == 4)
{
cin >> x;
int rk = Q1(l-1,r,x);
if(!rk) cout << "-2147483647" << '\n';
else cout << Q(l-1,r,rk) << '\n';
}
if(op == 5)
{
cin >> x;
int rk = Q1(l-1,r,x+1);
if(rk == r-l+1) cout << "2147483647" << '\n';
else cout << Q(l-1,r,rk+1) << '\n';
}
}
return 0;
}
换成 01trie 就好了。
3.树状数组套vector
众所周知随机数据下 vector 是能过平衡树板题的。
大家应该都会。但还是看一下吧。
#include <bits/stdc++.h>
using namespace std;
vector< int >v;
int main()
{
int n;scanf("%d",&n);
for(int i = 1;i <= n;i++)
{
int op,x;scanf("%d%d",&op,&x);
if(op == 1) v.insert(lower_bound(v.begin(),v.end(),x),x);
if(op == 2) v.erase(lower_bound(v.begin(),v.end(),x));
if(op == 3) printf("%d\n",lower_bound(v.begin(),v.end(),x)-v.begin()+1);
if(op == 4) printf("%d\n",v[x-1]);
if(op == 5) printf("%d\n",v[lower_bound(v.begin(),v.end(),x)-v.begin()-1]);
if(op == 6) printf("%d\n",v[upper_bound(v.begin(),v.end(),x)-v.begin()]);
}
return 0;
}
回到这个题。
把 fhq 换成vector,然后你就过了。
int n,m,a[N];
vector < int > v[N];
int Q(int l,int r,int k)
{
int sum = 0;
while(r) sum += upper_bound(v[r].begin(),v[r].end(),k)-v[r].begin(),r -= r&-r;
while(l) sum -= upper_bound(v[l].begin(),v[l].end(),k)-v[l].begin(),l -= l&-l;
return sum;
}
void add(int i,int a,int b)
{
while(i <= n)
{
if(~a) v[i].erase(lower_bound(v[i].begin(),v[i].end(),a));
v[i].insert(lower_bound(v[i].begin(),v[i].end(),b),b);
i += i&-i;
}
}
这时候就能发现有时不是 \(\log^3\) 的问题,而是常数的问题。
跑的比 01trie 还快。

上为 01trie,下为 vector
看这优秀的空间,知道改练谁了吧。
4.树状数组套线段树
还是这个题。
静态区间第 k 小大家都会写主席树。
那这个题不就是动态区间第 k 小吗?
静态区间求和是不是开个前缀和数组就行了?
动态区间求和是不是用树状数组维护一下就行了?
主席树不就相当于开了个前缀和数组方便快速求出区间信息吗?
那么把这个前缀和数组换成树状数组不就能维护动态区间信息吗?
大家应该能理解主席树就是数组套线段树吧。
说到这里大家应该已经听懂了吧。
操作基本没啥变化。
他们把这个称作动态主席树。
题意:
对于序列 \(a\),它的逆序对数定义为集合 $${(i,j)| i<j \wedge a_i > a_j }$$中的元素个数。
现在给出 \(1\sim n\) 的一个排列,按照某种顺序依次删除 \(m\) 个元素,你的任务是在每次删除一个元素之前统计整个序列的逆序对数。
对于 \(100\%\) 的数据,\(1\le n \le 10^5\),\(1\le m \le 50000\)。
Sol:
初始的逆序对数大家应该都会归并或树状数组吧?
考虑求出删数会减少的逆序对数减一下就是剩下的逆序对数。
怎么求减少的逆序对数呢?
假如我们要删 \(a[p] = k\),减少的其实就是满足 \(a_i > k ,i<p\) 和 \(a_i<k,i>p\) 的数。
这不就是查询区间内大于他或小于他的数的个数同时还带个修吗?
``Dynamic'' Inversion 喜闻乐见的经验。
题意:
排排坐,吃果果,生果甜嗦嗦,大家笑呵呵。你一个,我一个,大的分给你,小的留给我,吃完果果唱支歌,大家乐和和。
红星幼儿园的小朋友们排起了长长地队伍,准备吃果果。不过因为小朋友们的身高有所区别,排成的队伍高低错乱,极不美观。设第 \(i\) 个小朋友的身高为 \(h_i\)。
幼儿园阿姨每次会选出两个小朋友,交换他们的位置,请你帮忙计算出每次交换后,序列的逆序对数。为方便幼儿园阿姨统计,在未进行任何交换操作时,你也应该输出该序列的逆序对数。
对于100%的数据,\(1 \le m \le 2\times 10^3\),\(1 \le n \le 2 \times 10^4\),\(1 \le h_i \le 10^9\),\(a_i \ne b_i\),\(1 \le a_i,b_i \le n\)。
Sol:
思路和上道题一模一样,但是交换造成的逆序对数变化不同。
交换 x 位置和 y 位置的数,逆序对数加上 \([x,y-1]\) 里比 \(<a_y\) ,加上\([x+1,y]\)
贡献变为了页数和,在记录个数的时候额外记录一下页数和就好。
其实树套树还能处理好多偏序问题,出于篇幅原因请自行查阅。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号