二月——Week1
2025.2.03
A.长佳蕊 Mystery Square
钟:本地编译要开 c++14 和 O2,小心一些库和 __int128 的奇妙搭配产生绝妙 CE
根据数据范围可以想到折半,但和正常的折半好像不太相同。
如果高 \(\frac{n}{2}\) 位里不超过 20 个 ?,把前 \(\frac{n}{2}\) 位确定了,后面全填 0 直接开根得到的数和答案相差很小,\(O(1)\) 枚举可以解决。
难点在于低 \(\frac{n}{2}\) 位里不超过 20 个 ?,把低 \(\frac{n}{2}\) 位确定后,如何求出 \(\sqrt s\)。
首先把 \(s\) 末尾的 0 两两成对去掉(先开根开出去),因为保证有解,最后末尾剩下的一定是 1。
由于我们是根据去除完末尾的 0 剩下的二进制串进行分讨操作,所以我们要枚举最后有多少个零,不然会导致去除末尾 0 之后,初始确定的低 \(\frac{n}{2}\) 位不再是当前二进制串的低 \(\frac{n}{2}\) 位。
目前唯一的问题就是如何确定 \(\sqrt s\) 了。
若我们现在在确定 \(x=\sqrt s\) 的二进制低 \(i\) 位,也就是说第 \(1\sim i-1\) 位都确定好了,也就是说现在还能改变 \(x^2\) 低 \(i+1\) 位的只有尚未确定的 \(x\) 的低 \(i\) 位,而根据列竖式可得,若 \(x\) 的低 \(i\) 位填 \(1\),对 \(s\) 的低 \(i\) 位没有影响,向低 \(i+1\) 位进一,所以根据当前 \(x^2\) 和 \(s\) 的低 \(i+1\) 位是否相同来确定 \(x\) 低 \(i\) 位应该填什么。
感觉思维难度比较大。
B.有趣的游戏 Game of Slots
Alice 从小到大,Bob 从后往前田忌赛马这个策略比较显然。
值域 \(10^{18}\) 不好处理,肯定要离散化为 \([1,2n]\),这时候若不存在相同的数,每种情况都是等概率发生。若存在相同的数,会发现我们把存在相同的数的概率算大了。但是仔细一想会发现离散化前存在相同的数的概率约为 \(0.99999999999998010001\),乘了贡献变成期望之后也很小,对保留 \(6\) 位小数的答案没有任何影响,所以我们索性直接排除存在相同数的情况。
我到这里直接顺序搜索 Alice 分到了什么,Bob 分到的就是剩下 \(n\) 个数,很不好优化。
由 Bob 从后往前田忌赛马的策略,发现从后往前倒序确定每个数分配给谁就可以很好的 dp。
具体的,规定 \(0\) 代表分给 Alice,\(1\) 代表分给 Bob,设 \(f_{i,j,k}\) 为填了 \(i\) 个 \(0\),\(j\) 个 \(1\),Bob 还有 \(k\) 个 \(1\) 的 Alice 得分总和,\(g_{i,j,k}\) 代表方案数。
如果当前这个数填 \(1\)(分给 Bob),则 \(f_{i,j+1,k+1}\gets f_{i,j+1,k+1}+f_{i,j,k},g_{i,j+1,k+1}\gets g_{i,j+1,k+1}+g_{i,j,k}\)。
否则填 \(0\)(分给 Alice),若 \(k>0\),此时这个数会被 Bob 剩的数解决掉,\(f_{i,j+1,k-1}\gets f_{i,j+1,k-1}+f_{i,j,k},g_{i,j+1,k-1}\gets g_{i,j+1,k-1}+g_{i,j,k}\)。
否则 \(k=0\),不会被解决掉,Alice 在这一位 > Bob,获得贡献,\(f_{i+1,j,0}\gets f_{i+1,j,0}+f_{i,j,0}+(n-i)\times g_{i,j,0},g_{i+1,j,0}\gets g_{i+1,j,0}+g_{i,j,0}\)。
问题就解决掉了,难点好像并不在于 dp,虽然我是卡在 dp 上了。
C.矩阵 RowCol/ColRow Sort
部分分:若 \(\max{b_{i,j}}\le 1\),其实就是规定有若干个 \(1\) 的行有多少个,若干个 \(1\) 的列有多少个,这两个问题是分别独立的,多重集排列数之后乘起来。
2025.2.04
A: 棋子
绝妙 Trick:一个矩形的四个角的问题考虑最小生成树。
对于 \((i,j)\),若存在 \((x,y)\) 使得 \((x,y),(x,j),(i,y)\) 都有棋子则 \((i,j)\) 也有棋子。
对于有棋子的 \((x,y)\),我们添加一条 \(x\) 和 \(y+n\) 的边,这时候我们惊喜的发现上述情况下 \(i\) 和 \(j+n\) 连通,然后可以直接建图跑最小生成树了。
赛时没往图论上面想,一直在暴力维护这个东西,导致没有写出来。发现正常写很难维护的时候应该考虑一下别的角度。
B: 序列
\(O(n^2)\) 暴力想到之后应该比较容易想到和回文串类似进而使用 manacher 优化的。
暴力就是枚举串的中心暴力向两侧扩展,这时候会发现我们在进行类似暴力统计回文串的过程,进而考虑是否能套用 manacher 来对我们这个过程进行优化呢?
可以先试试。
同样的,我们记录右端点最远的中心 \(mid\),对于当前我们要扩展的 \(i\),若 \(i\le mid+r_{mid}-1\),那我们就把 \(2\times mid-i\) 位置的信息拿过来。
我们需要的信息有 \(c_i\) 代表以 \(i\) 为中心的最长串包含的不同数字的个数,\(s_i\) 代表以 \(i\) 为中心的所有合法串的权值和。
若 \(i+r_i>mid+r_mid\) 我们要先在 \(2\times mid-i\) 处,把半径缩短。
然后我们要对当前 \(i\) 尝试向外扩展。
统计不同数字个数可以预处理出 \(pre\) 和 \(nxt\) 数组,分别代表 \(a_i\) 上一次和下一次出现的位置。
判断新加进来数字之后串是否合法同样根据 \(pre\) 和 \(nxt\) 来判断。
现在问题是为什么可以类似 manacher 这么做。
因为以 \(2\times mid-i\) 的串关于 \(mid\) 对称过来之后,其实就是对串进行了一个置换,也就是将一个数字替换成另一个数字,而整体做这样的替换并不会影响数字的对应关系,所以是正确的。
C: 变换
部分分:
\(n\) 个数中任选 \(m\) 个数的乘积的和:生成函数,分治 NTT。
2025.2.05
A: 随机
每个点保留与之相连的最小的边,所以最多只会保留 \(n\) 条边。但是由于全局最小值 \(1\) 肯定会被统计两次,所以最多只能保留 \(n-1\) 条边,同时我们要求图联通,所以图最后一定是一棵树。
考虑从小到大加入边,加入 \(1\) 边之后,后面加入的每条边至少有一个端点与 \(1\) 边所在连通块相连,否则这条边也会至少被统计两次,导致图不连通。从另一个角度想,当前这条边新开了一个连通块,那么后面没有任何一条边能把当前连通块和 \(1\) 边所在连通块联通,最终结果也是图不连通。
所以我们设 \(f_{i,j}\) 表示加入了前 \(i\) 条边,\(1\) 边所在连通块大小为 \(j\) 的方案数,转移分为两种:
- 一个端点在 \(1\) 边所在连通块中:\(f_{i,j} = f_{i-1,j-1}\times(j-1)(n-j+1)\)
- 两个端点均在 \(1\) 边所在连通块中:\(f_{i,j} = f_{i-1,j}\times(\frac{j(j-1)}{2}-(i-1))\)
总体来说比较简单,不知道为什么赛时分析出比较关键的从小到大加边之后后面本来很简单的东西思考的有点混乱,可能也是对自己没有自信认为自己做不出来就去写其他题了,由此观之:保持清醒理智的头脑相当重要。
B: 替换
上 AC 自动机求出 \(S\) 每个位置匹配的长度最短的 \(T\) 串比较容易想到。
暴力是从 \(l\) 扫到 \(r\),每匹配到一个与上一个串不交的串便计入答案,时间复杂度 \(O(n^2)\)。
后面一个可能的想法是扫描线右端点 \(r\) 同时用线段树维护每个 \(l\) 对应的答案,具体实现就是对于新加入的 \(r\),将结尾位置 \(\le r-len_r\) 的全都更新成 \(r\),同时答案加一。比较尴尬的一点是这个东西不能用单调栈维护,只能使用线段树暴力维护,时间复杂度 \(O(n^2\log n)\),但是随机数据下表现优异。
上面就是赛时思路了。
正解是从一个位置开始向后选的方案是恒定的,所以可以倍增维护,时间复杂度 \(O(n\log n)\)。
赛时执着于扫描线线段树单调栈导致没往倍增方面想,一个很值得记住的教训就是如果赛时思路怎么都无法向下进行了,应该冷静下来思考一下别的方向,或许题目没有想象中的那么难,同时碰到这种端点固定方案就确定的之类的问题一定一定要考虑倍增。
C: 游走
\(O(n^3)\) 暴力很好想,赛时一直试图优化成 \(O(n^2)\),最后浪费了大量时间优化成了 \(O(n^2\log n)\) 获得了和暴力一样的分数,之后要注意避免这种问题,没有把握多拿分就不要浪费时间。
正解也不算不平凡,打表或者手玩能发现图被分成若干条链,一条链是一个等差数列。
而这些链有三种:一种是从第一列到第 \(n\) 行,一种是从第一行到第 \(n\) 列,一种是从第一列到第 \(n\) 列。
接下来分这三类来进行求解。
- 第一列到第 \(n\) 行
向下的步数是 \(\frac{n-1}{k-1}\) 量级的,所以可以暴力枚举向下走的步数 \(s\),那么向右走的步数可推得为 \(s(k-1)-(n-s)\%P\),判断一下 \(s(k-1)-(n-s)\%P\) 是否 \(<n-1\) 即可。不过要注意的是我们要统计的是一整条链,也就是说起始的位置应为一条链的开头,例如下图中我们从 \((5,1)\) 开始走的那条链不应该被统计,因为它属于 \((4,1)\) 那条链,不然会算重。
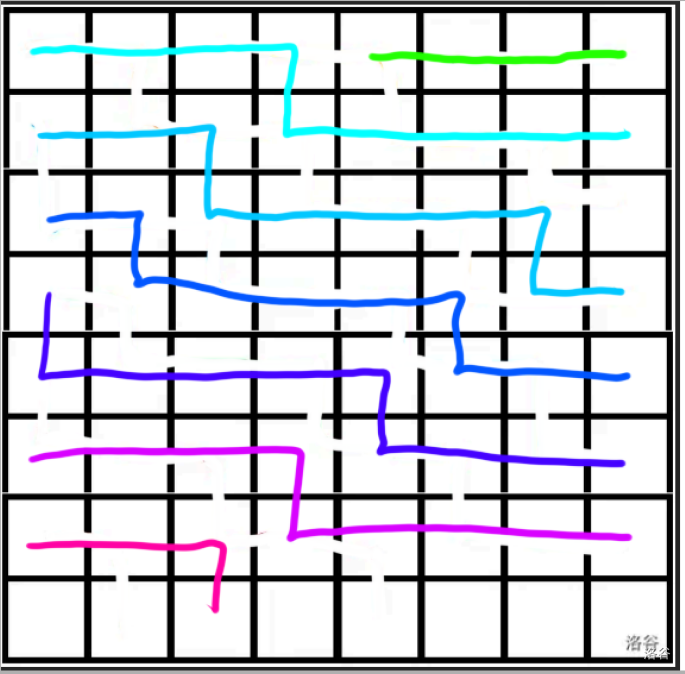
- 第一行到第 \(n\) 列
\(1+y\equiv0\pmod k\) 的位置是向下的拐点,所以 \(1+y\equiv1\pmod k\) 也就是 \(y\equiv0\pmod k\) 的位置是一条链的起点,这个同样是 \(\frac{n}{k}\) 量级的,同样可以暴力枚举起点 \((1,y)\),那么拐点就是 \((1,y+k-1)\),而拐点之后的路径也是恒定的,可求得向下走的次数为 \(\lceil\frac{n-(y+k-1)}{k-1}\rceil\),向右走的次数就是 \(n-y\)。 - 第一列到第 \(n\) 列
链的高度(向下走的次数)为 \(\lfloor\frac{n-1}{k-1}\rfloor\) 或 \(\lfloor\frac{n-1}{k-1}\rfloor+1\),而向右的次数是固定的 \(n-1\),接下来只需要统计这两种链的个数。
设起点为 \((x,1)\),那么我们要先向右走 \(k-x\%k-1\) 步走到 \(x+y\equiv0\pmod k\) 的位置,后面的轨迹就有规律了,求得向下走的次数为 \(\lfloor\frac{n-1+x\%k-1}{k-1}\rfloor\),列等式:\[\lfloor\frac{n-1+x\%k-1}{k-1}\rfloor=\lfloor\frac{n-1}{k-1}\rfloor \]解得 \(x\%k\le k-1-(n-1)\%(k-1)=L\),而在第一类的枚举是我们能求出 \(x\in[1,p]\) 时可以走到第 \(n\) 列。
求出满足上方不等式的 \(x\) 数量 \(c\) 为 \(\lfloor\frac{p}{k}\rfloor(L+1)+\min(p\%k,L)\)。
所以长度为 \(\lfloor\frac{n-1}{k-1}\rfloor+1\) 的链的个数为 \(p-c\),而长度为 \(\lfloor\frac{n-1}{k-1}\rfloor\) 的链的个数还要减去非链头的起点(\(x+1\equiv1\pmod k\) 即 \(x\equiv0\pmod k\))的地方,答案是 \(c-\lfloor\frac{p}{k}\rfloor\)。
至此,大功告成。
这种题尽管不难理解但是赛时大概率是写不出来的,尽量多拿暴力分吧。
D: 树上最小连通块
若颜色数较少可以直接状压树形 dp,赛时只进行到这。
但是问题是若颜色数是 \(O(n)\) 量级的怎么办?
一个非常厉害的思路就是给颜色 \(1\) 到 \(n\) 随机分配一个 \(\le k\) 的权值 \(val\),这样只会让原来不同的颜色变得相同,也就是说我们最后统计的当前连通块的颜色数只会减少而不会增多。
考虑这样什么时候是正确的。
假设最优解包含的是 \(a,b,c,d,e\) 这 \(5\) 种颜色,若给他们分配的 \(\le k\) 的权值也互不相同那么我们 dp 求得的答案就是正确的,而这样的概率是 \(\frac{5!}{5^5}=0.192\),多随机几次就可以通过了。
这种思路应该积累,有时候适当的抛弃正确性反而会让思路打开柳暗花明。
2025.2.06
A: 路径
签到题,树剖之后线段树 pushup 维护区间的最大值最小值以及答案即可,时间复杂度 \(O(n\log^2 n)\)。
还可以使用倍增,记 \(mx_{i,x}\) 为从 \(x\) 向上跳 \(2^j\) 步经过结点权值最大值,\(mn_{i,x},ans_{i,x},fa_{i,x}\) 同理,时间复杂度 \(O(n\log n)\),但是跑的没树剖快。
赛时一开始想了十几分钟的扫描线单调栈线段树写法,发现只能处理序列,放到树上复杂度不对。
B: 迷失
这种图的周期问题,首先一定要想到找环,因为只有环才有周期。
而在有向图中,强连通分量彼此是单向的,互不影响,所以最后答案的周期应该是所有强连通分量周期的 \(\operatorname{lcm}\)。
一个强连通分量的周期是什么?结论是强连通分量内所有环的长度的 \(\gcd\)。
这里感性证明一下:
记 \(d\) 为强连通分量内所有环的长度的 \(\gcd\),那么我们选取一点为起点对图中的点重新标号,标号为起点到它的距离 \(\bmod d\)。
由于所有环长都是 \(d\) 的倍数,所以每个结点的标号是唯一的。
而我们的 \(A^k\) 的矩阵 \(a_{i,j}\) 的取值代表从 \(i\) 结点开始走 \(k\) 步能否到达 \(j\) 结点。
我们对单独一个结点来考虑,设他的新标号为 \(x\),那么他下一步会走到若干编号为 \((x+1)\bmod d\) 的结点,以此类推。
而根据强连通分量的性质,从一个点出发能遍历到强连通分量内所有的结点,也就是说走若干步之后,\(x\) 能到达点的集合一定包含所有新标号为 \(y\) 的点,而所有新标号为 \(y\) 的点下一步一定能走到所有新标号为 \((y+1)\bmod k\) 的点,就此进入周期。
这样有向图的周期问题就被我们解决了。
关于走多少步(记为 \(k\))才能进入周期这个问题,显然满足可二分性。不过因为我们并不清楚二分上界,所以可以倍增实现,总时间复杂度 \(O(\log k\frac{n^3}{w})\)
赛时在找环这一部分想了一段时间,被找出图的所有环的环长吓到了,最后发现最简单的 dfs 就能解决这个问题,下次应该就不会忘了。
C: 异或
赛时感觉一点思路没有,根据经验碰到这种一点思路没有情况巨复杂不太能分析的题应该猜点结论。
于是我猜一个路径肯定是删路径上边权最大的边,猜了之后每次就可以暴力 \(O(n^2)\) 枚举点对求答案了,时间复杂度 \(O(n^3)\),用边分治可能可以优化到 \(O(n^2\log n\log V)\)。
因为猜到的结论虽然是对的,但是跟正解一点关系都没有,所以很难进行优化。
正解是观察到操作并不会使两点间的路径异或和发生变化,所以把两点间的路径异或和当作两点间的边权跑最小生成树,那么最后添加的边一定是在最小生成树上的边,证明的话就是若添加一条不在最小生成树上的边,那么删去的那条边原本一定可以被一条在最小生成树上的边删去。
因为添加的那条不在最小生成树上的边 \((u,v)\) 不在最小生成树上,代表最小生成树上 \((u,v)\) 是联通的,那么最小生成树上 \((u,v)\) 之间的路径对应到原树上是一定跨过原树 \((u,v)\) 路径上的边的。
证明完了之后,我们可以先用 Boruvka 求出完全图的最小生成树。
原树上的边集记为 \(A\),最小生成树上的边集记为 \(B\),那么对于每个 \(k\) 其实就是求恰有 \(k\) 条 \(B\) 边的最小生成树权值和,这个是经典问题 [国家集训队] Tree I。
但是对于每个 \(k\) 都进行 wqs 二分的话,时间复杂度是 \(O(n^2\log V)\),不能通过,所以要进行整体 wqs 二分。
过程就是在当前层跑完最小生成树之后,边集分为 \(a_0\) 代表原树中且未在当前最小生成树的边,同理可得 \(a_1,b_0,b_1\)。
对于向左递归(缩小加权/二分上界)的那一层,由于给 \(B\) 边的加权减小,那么当前在 \(a_0\) 的边一定不会再加入最小生成树,当前在 \(b_1\) 的边一定还在最小生成树中,所以将 \(a_1,b_0\) 递归下去即可。
同理向右递归时将 \(a_0,b_1\) 递归下去即可。
由于递归需要回溯,所以最小生成树过程使用可撤销并查集。
最小生成树过程中若 \(A\) 中边权值和 \(B\) 的权值相同,可以优先加入 \(A\) 中的边。这样方便后面解决 wqs 二分加权变化使得最小生成树中 \(B\) 边数量变化并不连续的问题。
2025.2.07
A: 袭击
赛时推的式子复杂且有精度问题,放个题解的式子。
首先,假设打袭击的人在位置 \((0,0)\),有一个在 \((x_1,y_1)\) 的袭击者,方向、速度分别为 \(t,v_1\)。
不妨设火球会在 \((x_2,y_2)\) 打中,且这个位置与袭击者最开始的位置的距离为 \(k\)。
于是有:
由于 \(v_0>v_1\),所以分母为正数,且 \(x_1\cos t+y_1\sin t<\sqrt{(x_1\cos t+y_1\sin t)^2+\dfrac{v_0^2-v_1^2}{v_1^2}(x_1^2+y_1^2)}\)。
所以正负号只能取正(否则 \(k\) 就是负数)。
所以:
火球飞的时间就是:
再回到原题,假设人在 \((x_0,0)\),那么每个火球飞的最长时间就是:
考虑到正常考试肯定不会选择模拟退火作为正解,大胆猜测这个东西是关于初始位置 \(x_0\) 单峰的,于是就可以三分了。
以后比赛时推式子的时候尽量选择向容易化简,精度误差小的方向去推,什么都不想只会力大砖飞暴力推只会让分数更低。
B: 前后缀
场切了,爆标了,感觉不是很难。
字符串计数题去重有两大招:
- 一种是将重复计算的减去
- 另一种是钦定在某个位置(第一次出现/最后一次出现)计数
这里我用的是第一种。
首先因为是前缀问题,先给正串建个 Trie 树,记为 \(A\),给反串建个 AC 自动机,记为 \(B\)。
考虑什么样的字符串会被重复计算,我们将最后的字符串划分成三部分。

若正串同时有 \(P\) 和 \(P+Q\),且反串同时有 \(Q+R\) 和 \(R\) ,那么 \(P+Q+R\) 我们会在 \(P+(Q+R)\) 和 \((P+Q)+R\) 同时统计到。
如何将这种情况造成的重复计数减去?
我们考虑 \(B\) 上每个结点代表的字符串减去其在 fail 树上的父节点代表的字符串(即删除最长公共后缀)剩下的这样一个字符串,如果形如这样的字符串是我们当前枚举正串的前缀的一个后缀,是不是代表着我们当前的前缀为 \(P+Q\),也就代表着当我们前缀为 \(P\) 的时候已经和 \(Q+R\) 拼过一次了,所以现在 \(P+Q\) 就不能和 \(R\) 再拼了。
所有我们把上述字符串都拿出来建一个 AC 自动机,之后在枚举正串的前缀时,在新建的 AC 自动机上跑,当前前缀在 AC 自动机上的到根链和就是当前正串前缀匹配的字符串 \(Q\) 的个数,减去他就好了。
至于为什么只用把当前节点 \(x\) 减去父节点 \(fa_x\) 的字符串拿出来而不用一直跳 fail,是因为我们在处理到 \(fa_x\) 的时候同样会把 \(fa_x\) 减去 \(fa_{fa_x}\) 剩下的的字符串加入 AC 自动机,这个显然是 \(x\) 减去 \(fa_{fa_x}\) 剩下的字符串的后缀。所以我们只加入本质不同的最短的串即可。
在实现上,如果我们真的把这些串拿出来新建 AC 自动机的话,这些串的总长是 \(O(n^2)\) 量级的,不可接受。但是发现这些串其实也是我们反串的前缀,所以只需要在 \(B\) 的 Trie 树上把没用的结点删去同时对 \(B\) 重新建一遍 AC 自动机就好。
最后统计答案的时候注意我们的答案串是由正串的非空前缀和反串的非空前缀拼起来的,不要多减。
2025.2.08
有点像简单 adhoc 题专场。
A: 多项式多点求值
这道题转移关系构成一棵二叉树,通过手玩或者暴力能很容易知道一个点对应的值域是连续的。
我们要知道一个点对应的值域代表着什么。下界 \(l\) 代表这个点能取到的最小值为 \(l\),同时也代表着要取到 \(l\) 这个最小值至少需要 \([1,l]\) 这些数。后面的这个性质是及其关键的,我赛时三个小时就是没想到后面这个意义被卡住了。上界 \(r\) 也就同理了。
知道了一个点的值域的意义,剩下的问题就是合并两个儿子。
这两个儿子的值域分别是 \([l_1,r_1],[l_2,r_2]\) 。
- 若当前为 \(\max\) 结点,那么当前节点值域为 \([l_1+l_2,\max(r_1,r_2)]\)。
- 若当前为 \(\min\) 结点,那么当前节点值域为 \([\min(l_1,l_2),r_1+r_2-n-1]\)。
然后这道题就完成了。感觉这种题确实是对我的思维水平来说有些困难,若赛时的思维比较迟钝的话是不太可能想到后面那个意义的。
B: 真随机数生成器
发现删除一个数只会在处理到这个数在序列中最后一次出现的位置的时候才发挥作用,而且竟然是基本相同的子问题。
然后就可以从后向前来一个 \(O(v^2)\) 的 dp,需要注意的是 \(a_1\) 是一直都有的,在任何位置都可以随机选到 \(a_1\) 来结束战斗。
写完 \(O(v^2)\) 的 dp 之后会发现答案数组 \(f_i\) 对前面的贡献系数是 \(i\) 的出现次数,额外向后的 \(O(v)\) 枚举是完全不必要的,之后就能优化成 \(O(n)\) 了。
C: 快速高斯消元
赛时设了 \(f_{n,m}\) 代表 \(n\) 个人最后编号为 \(m\) 的人最后活下来的概率,发现转移成环了,而且忘记这种成环的转移怎么高斯消元了,应该是丢了 60 分,回头要复习一下转移成环的 dp。
正解是设 \(f_{n,i}\) 表示 \(n\) 个人时第一个出局的是 \(i\) 的概率,这个是等比数列求和。
然后设 \(g_{n,i}\) 表示 \(n\) 个人最后存活的是 \(i\) 的概率,那么 \(g_{i,j}=\sum\limits_{k=1}^{i}f_{i,k}g_{i-1,(j-k)\bmod\ i}\)。
发现 \(f\) 的值呈现一定规律,有值的两个位置间隔是 \(d=\gcd(n,k)\),可以把所有的 \(g\) 按第二维下标 \(\bmod d\) 分类,同一类一起处理。
具体的,\(f\) 除了环上最后一个点 \(f_{n,0}\),其他在环上的点的值都是环上后继的 \(2\) 倍,所以我们可以对 \(g\) 的每一类暴力求出来第一个,之后就可以在环上跳前驱来更新。
这道题比较难的点是想出来辅助数组 \(f_{n,i}\),这样用类似强制添加/删去一个人的操作就完美的解决了转移成环的问题,比较厉害。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号