经典dp问题

本人的第一篇博客，记录一些经典dp问题

---

lis（最长上升子序列）

给定一个长为n的序列ai,求这个序列的最长单调上升子序列长度
例：a={1，2，4，1，3，4}
做法一（n^2）
设dp[i]=以a[i]结尾的子序列中，最长的上升子序列的长度
如在该例子中dp={1，2，3，1，3，4}；
动态转移方程：dp[i]=max(dp[j]+1)(j<i,a[j]<a[i])

点击查看代码

#include <iostream>
using namespace std;
const int N=5010;
int a[N],dp[N];
int main(){
    int n,ans=1;
    cin>>n;
    for(int i=1;i<=n;++i) cin>>a[i],dp[i]=1;
    for(int i=2;i<=n;++i){
        for(int j=1;j<=i-1;++j){
            if(a[j]<a[i]) dp[i]=max(dp[i],dp[j]+1);
        }
        ans=max(ans,dp[i]);
    }
    cout<<ans;
    
    return 0;
}

做法二（nlogn)
试着反过来思考，设dp[i]=长度为i的上升子序列的结尾的最小元素
如在该例子中dp={1，2，3，4，∞，∞}；
可以发现该数组是单调递增的
不妨考虑从小到大递推，二分dp中最大的小于a[i]的dp[j]，更新dp[j+1]

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],b[N],dp[N],ys[N],ans;
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;++i) cin>>a[i];
	memset(dp,0x3f,sizeof(dp)); dp[0]=0;
	for(int i=1,j;i<=n;++i){
		j=lower_bound(dp+1,dp+n+1,a[i])-dp; j--;
		dp[j+1]=min(dp[j+1],a[i]);
		ans=max(ans,j+1);
	}
	cout<<ans;
    
    return 0;
}

例题一（n^2)
例题二(nlogn)
例题三（本题是lcs的模板题，但正解实则是用lis）

---

lcs（最长公共子序列）

给定长为n的序列a，长为m的序列b,求这两个序列的最长公共子序列的长度
例：a={1，3，7，4，9，5},b={5，3，4，6，9，1，7}
做法（n^2）
设dp[i][j]=a[i..n]与b[j..m]的最长公共子序列长度
考虑动态转移方程
当a[i]=b[j]时,dp[i][j]=dp[i+1][j+1]+1

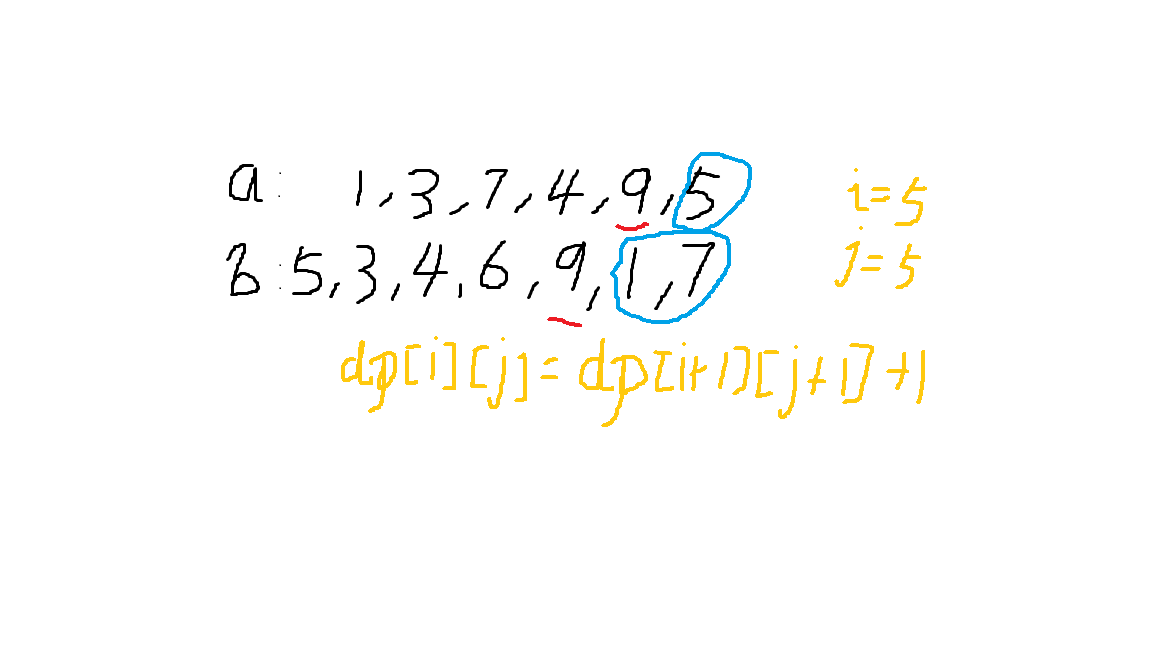
可以看作为将a[i],b[j]删掉(图中红色部分），那么剩下的最长公共子序列的长度就等于dp[i+1][j+1]
当a[i]=b[j]时,dp[i][j]=max(dp[i][j+1],dp[i+1][j])

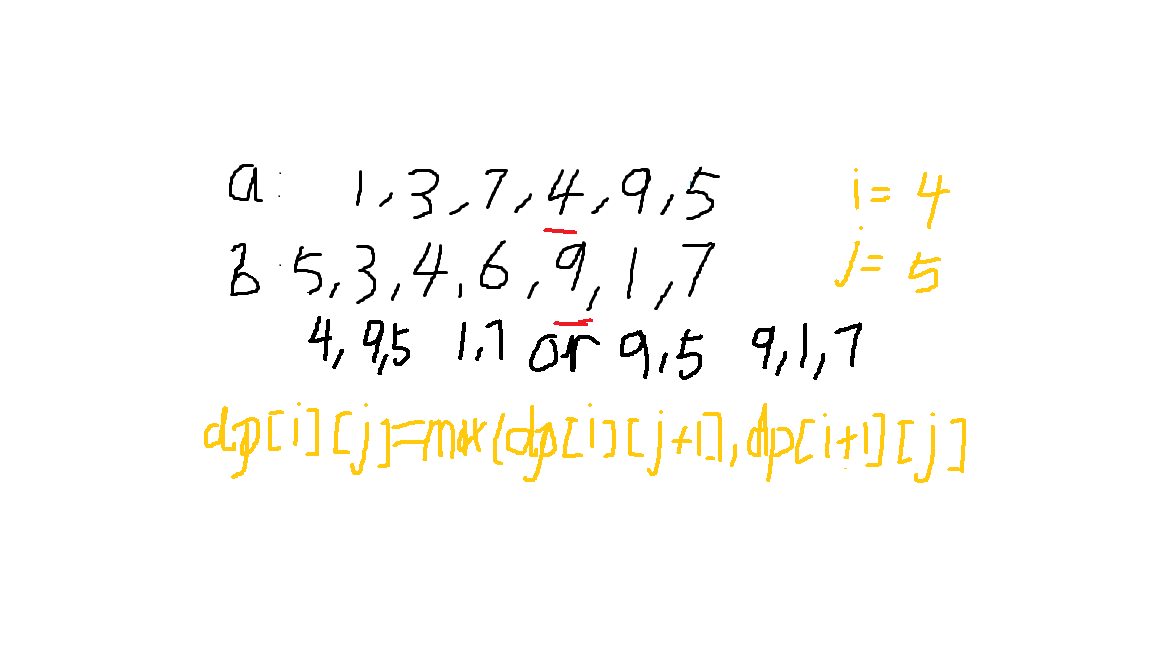
可以看作为将a[i]或b[j]删掉(图中红色部分），那么剩下的最长公共子序列的长度就等于max(dp[i+1][j],dp[i][j+1])

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e3+10;//50%
int a[N],b[N],dp[N][N];
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;++i) cin>>a[i];
	for(int i=1;i<=n;++i) cin>>b[i];
	for(int i=n;i>=1;--i){
		for(int j=n;j>=1;--j){
			if(a[i]==b[j]) dp[i][j]=dp[i+1][j+1]+1;
			else dp[i][j]=max(dp[i+1][j],dp[i][j+1]);
		}
	}
	cout<<dp[1][1];
    
    return 0;
}

例题一（前五十分，正解不是lcs，该题虽题名为模板题，但正解并不具有处理lcs问题的普遍性意义）