分治策略--笔记
1、分治策略的基本思想
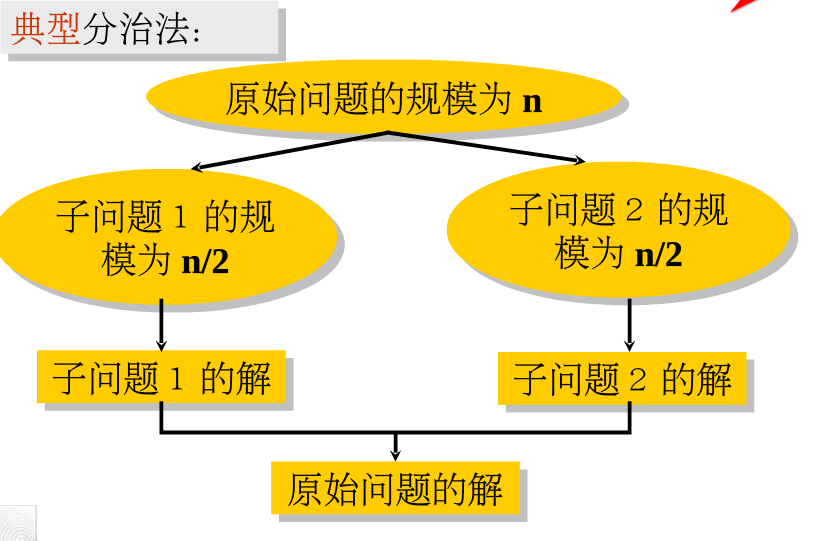
一个规模为n的问题可以分解为多个规模较小的子问题,每个子问题相互独立,并与原问题相同,最后将子问题的解合并可得原问题的解。
2、分治法的基本步骤
①分解 ②递归求解所有子问题 ③合并
分治思想的应用
1、大整数乘法
问题描述:在实际应用中,经常要使用两个很大的整数相乘(如密码技术中的RSA算法),而目前的机器硬件最多只能直接运算两个128位(二进制)的乘法,所以需要软件来运算。
传统算法:
时间复杂度
简单分治算法:
步骤:
1.切分产生A、B、C、D;
2.计算四个,n/2位乘法AC、AD、BC、BD (规模缩小的子问题);
3.计算三个加法、两次移位:AC左移n位,(AD+BC)左移n/2位
4.计算XY
复杂度分析:
此时时间复杂度可以表示为
•建立递归方程
T(n)= O(1) if n=1
T(n)=3T(n/2)+O(n) if n>1
•使用Master定理
T(n)=O(nlog3)=O(n1.59)
由此可见,算法的性能得到了提高。
2、Strassen矩阵乘法
问题描述:
n×n矩阵A和B的乘积矩阵C中的元素C[i,j]定义为:
传统算法:
用传统方法计算时,算法的时间复杂度为O(n3),原因:
分治法:
将矩阵A,B和C中每一矩阵都分块成4个大小相等的子矩阵(每个子矩阵都是n/2*n/2的方阵)。由此可将方程C=AB重写为:
由此可得:
复杂度分析:
根据Master定理可得 T(n)=O(n3) -> 分块并没有从本质上改进算法复杂度
(这里不太明白为什么子问题的个数为8???)
改进:
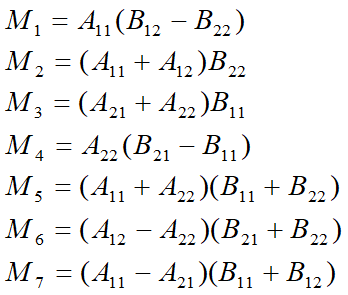

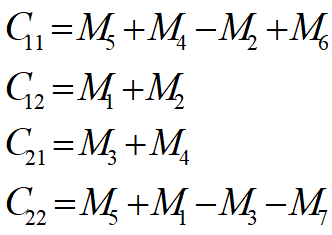
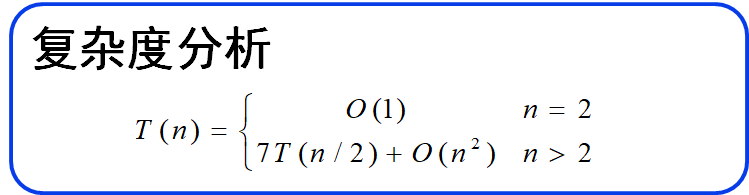
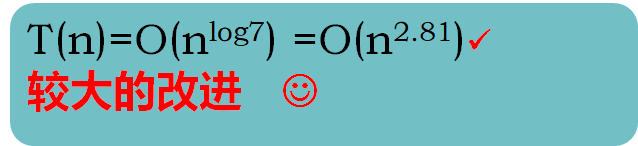
改善分治算法性能的途径
通过这两个例子,可以看到,可以通过减少子问题的个数,从而减小a,最终使得分治算法的时间复杂度的阶减小
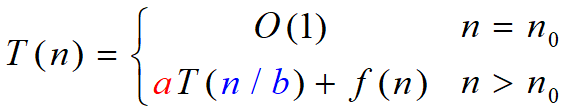
3、合并排序
基本思想:
将待排序元素集合分为大小相同的两个子集和,分别对两个子集合进行排序,最终将排好序的子集和合并成要求的排好序的集合。过程如下:
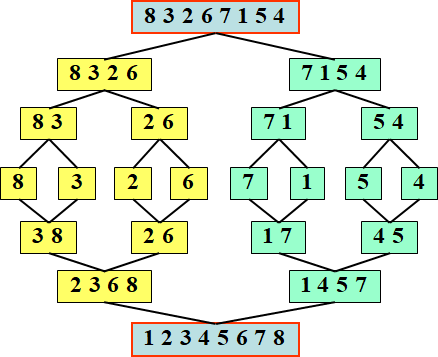

合并:

posted on 2020-10-25 18:06 CaRpe_DiEm2 阅读(361) 评论(0) 收藏 举报







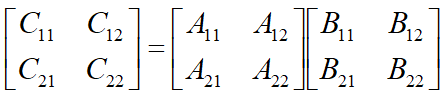

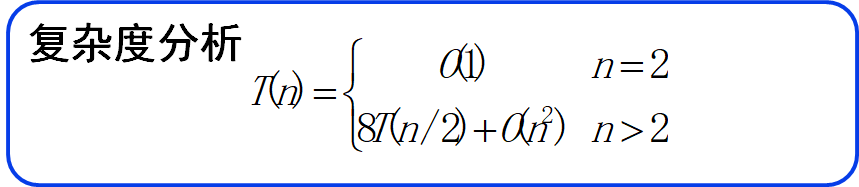

 浙公网安备 33010602011771号
浙公网安备 33010602011771号