机器学习应用(北理工)
一.机器学习准备
1.机器学习分类
- 监督学习
- 无监督学习
- 强化学习(增强学习)
- 半监督学习
- 深度学习
2.Python Scikit-learn
(1)简介
- http://scikit-learn.org/stable/
- 一组简单有效的工具集
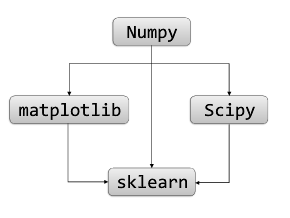
- 依赖
Python的NumPy,Scipy和matplotlib库
(2)常用函数
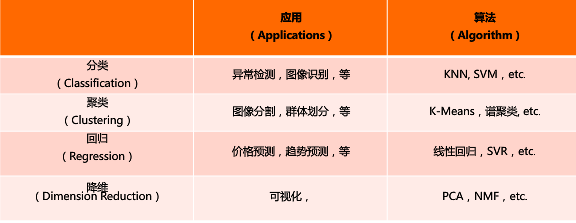
(3)sklearn库的安装
- 相关库安装
(4)sklearn库中的标准数据集
-
数据集总览
-
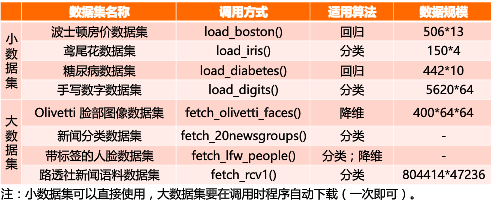
-
波士顿房价数据集
-
波士顿房价数据集包含506组数据,每条数据包含房屋以及房屋周围的详细信息。其中包括城镇犯罪率、一氧化氮浓度、住宅平均房间数、到中心区域的加权距离以及自住房平均房价等。因此,波士顿房价数据集能够应用到回归问题上。
-
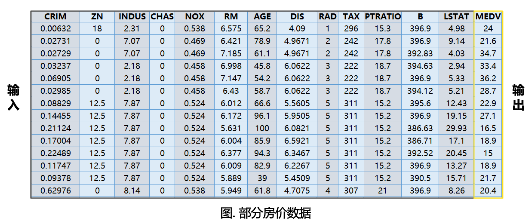
-
-
属性描述
-

-
数据集加载
sklearn.datasets.load_boston #使用此语句加载相关数据集 ''' 参数: return_X_y:表示是否返回 target(即价格),默认为 False,只返回data(即属性) '''-
数据集加载示例
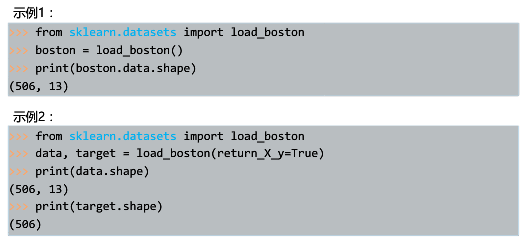
-
-
-
手写数字数据集
-
手写数字数据集包括1797个0-9的手写数字数据,每个数字由8*8大小的矩阵构成,矩阵中值的范围是0-16,代表颜色的深度。
-
数据集加载
sklearn.datasets.load_dights ''' 参数: return_X_y:若为True,则以(data, target)形式返回数据;默认为 False,表示以字典形式返回数据全部信息(包括data和target) n_class:表示返回数据的类别数,如:n_c1ass=5,则返回0到4的数据样本。 '''-
数据集加载示例
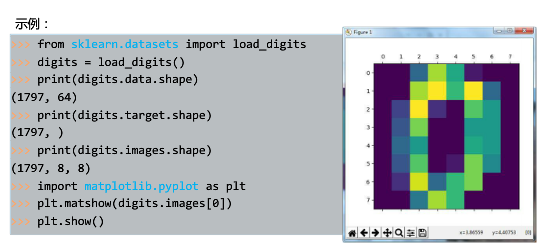
-
-
(5)sklearn库的基本功能
sklearn库的共分为6大部分,分别用于完成分类任务、回归任务、聚类任务、降维任务、模型选择以及教据的预处理,
-
分类任务
-
回归任务
-
聚类任务
-
降维任务
二.无监督学习
1.无监督学习简介
(1)简介
- 利用无标签的数据学习数据的分布或数据与数据之间的关系被称作无监督学习。
- 有监督学习和无监督学习的最大区别在于数据是否有标签
(2)无监督学习的应用场景
①聚类(clustering)
-
简介
- 聚类( clustering),就是根据数据的“相似性”将数据分为多类的过程。
- 评估两个不同样本之间的“相似性”,通常使用的方法就是计算两个样本之间的“距离”
使用不同的方法计算样本间的距离会关系到聚类结果的好坏。
-
欧氏距离
-
欧氏距离是最常用的一种距离度量方法,源于欧式空间中两点的距离。其计算方法如下:
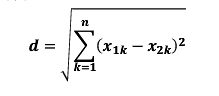
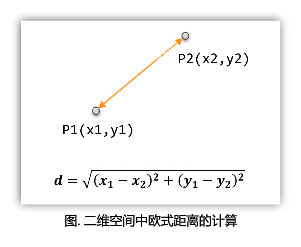
-
-
曼哈顿距离
-
曼哈顿距离也称作“城市街区距离”,类似于在城市之中驾车行驶,从一个十字路口到另外一个十字楼口的距离。其计算方法如下:
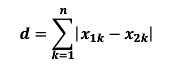

-
-
马氏距离
-
马氏距离表示数据的协方差距离,是一种尺度无关的度量方式。也就是说马氏距离会先将样本点的各个属性标准化,再计算样本间的距离。其计算方式如下:(s是协方差矩阵,如图)
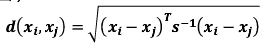

-
-
夹角余弦
-
余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个样本差异的大小。余弦值越接近1,说明两个向量夹角越接近0度,表明两个向量越相似。其计算方法如下:
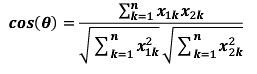

-
-
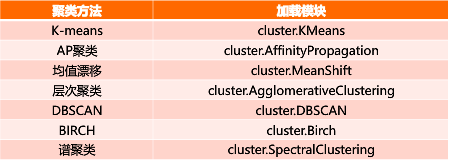
Sklearnvs.聚类- 常用聚类算法函数包含在
sklearn.cluster这个模块中,如:K- Means,近邻传播算法,DBSCAN,等 sklearn.cluster- sklearn. cluster模块提供的各聚类算法函数可以使用不同的数据形式作为输入:
- 标准数据输入格式:【样本个数,特征个数】定义的矩阵形式
- 相似性矩阵输入格式:即由【样本数目,样本数目】定义的矩阵形式,矩阵中的每一个元素为两个样本的相似度,如
DBSCAN, AffinityPropagation(近邻传播算法)接受这种输入。如果以余弦相似度为例,则对角线元素全为1.矩阵中每个元素的取值范围为【0,1】。 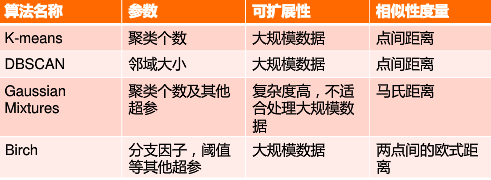
- sklearn. cluster模块提供的各聚类算法函数可以使用不同的数据形式作为输入:
- 常用聚类算法函数包含在
②降维
-
简介
- 降维,就是在保证数据所具有的代表性特性或者分布的情况下,将高维数据转化为低维数据的过程:
- 数据的可视化
- 精简数据
- 降维,就是在保证数据所具有的代表性特性或者分布的情况下,将高维数据转化为低维数据的过程:
-
聚类vs.降维
- 聚类和降维都是无监督学习的典型任务,任务之间存在关联,比如某些高维数据的聚类可以通过降维处理更好的获得。
-
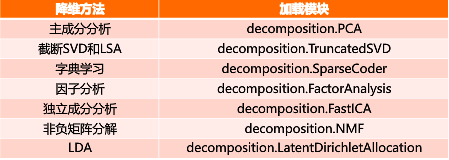
sklearn.decomposition模块-
降维过程也可以被理解为对数据集的组成成份进行分解( decomposition)的过程
-
对降维算法调用需要使用sklearn.decomposition模块

-
2.聚类
(1)K- means方法及应用
①K-means聚类算法
-
k- means算法以k为参数,把n个对象分成k个簇,使簇内具有较高的相似度,而簇间的相似度较低
-
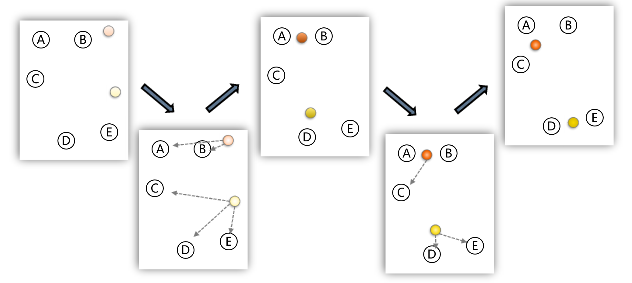
处理过程
-
随机选择k个点作为初始的聚类中心
-
对于剩下的点,根据其与聚类中心的距离,将其归入最近的簇
-
对每个簇,计算所有点的均值作为新的聚类中心
-
重复2、3直到聚类中心不再发生改变
-
(2)DBSCAN方法及应用
①DBSCAN密度聚类
-
DBSCAN算法是一种基于密度的聚类算法
- 聚类的时候不需要预先指定簇的个数
- 最终的簇的个数不定
-
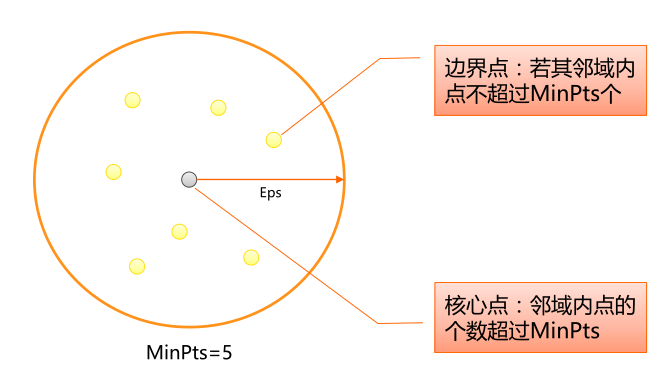
DBSCAN算法将数据点分为三类
-
核心点:在半径Eps内含有超过 MinPts数目的点
-
边界点:在半径Eps内点的数量小于MinPts,但是落在核心点的邻域内
-
噪音点:既不是核心点也不是边界点的点
-
-
DBSCAN算法流程:
- 1.将所有点标记为核心点、边界点或噪声点
- 2.删除噪声点
- 3.为距离在Eps之内的所有核心点之间赋予一条边
- 4.每组连通的核心点形成一个簇
- 5.将每个边界点指派到一个与之关联的核心点的簇中(哪一个核心点的半径范围之内)
-
算法详解
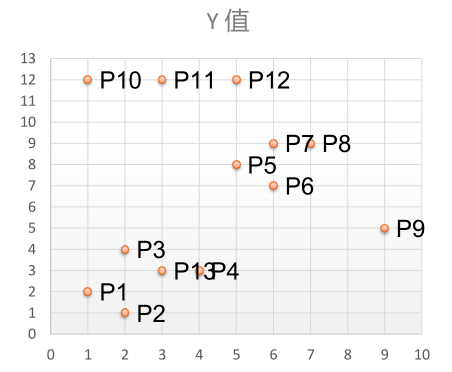
- 举例:有如下13个样本点,使用DBSCAN进行聚类
- 取Eps=3,MinPts=3,依据DBSACN对所有点进行聚类(曼哈顿距离)
- 举例:有如下13个样本点,使用DBSCAN进行聚类
-
核心点、噪声点、边界点
-
对每个点计算其邻域Eps=3内的点的集合
-
集合内点的个数超过MinPts=3的点为核心点
-
查看剩余点是否在核心点的邻域内,若在,则为边界点,否
则为噪声点。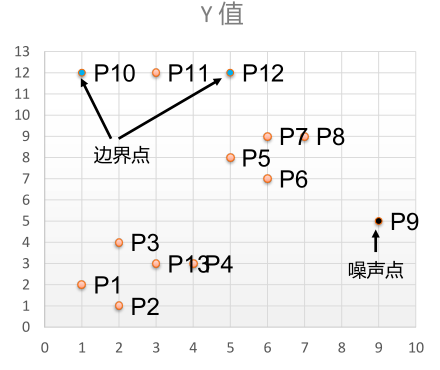
-
-
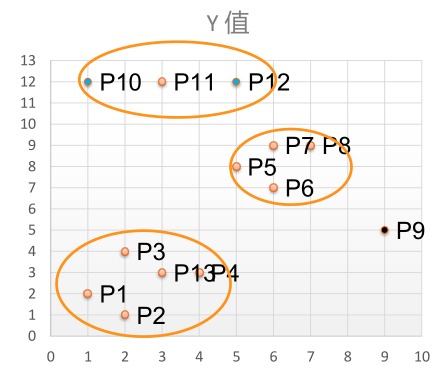
将距离不超过Eps=3的点相互连接,构成一个簇,核心点邻域
内的点也会被加入到这个簇中。则右侧形成3个簇
三.有监督学习
1.有监督学习介绍
(1)监督学习的目标
- 利用一组带有标签的数据,学习从输入到输出的映射,然后将这种映射关系应用到未知数据上,达到分类或回归的目的
- 分类:当输出是离散的,学习任务为分类任务
- 回归:当输出是连续的,学习任务为回归任务
(2)分类
-
分类学习
- 输入:一组有标签的训练数据(也称观察和评估),标签表明了这些数据(观察)的所署类别
- 输出:分类模型根据这些训练数据,训练自己的模型参数,学习出一个适合这组数据的分类器,当有新数据(非训练数据)需要进行类别判断,就可以将这组新数据作为输入送给学好的分类器进行判断
-
分类学习-评价
- 训练集(training set):顾名思义用来训练模型的已标注数据,用来建立模型,发现规律
- 测试集(testing set):也是已标注数据,通常做法是将标注隐藏,输送给训练好的模型,通过结果与真实标注进行对比,评估模型的学习能力
- 训练集/测试集的划分方法
- 根据已有标注数据,随机选出一部分数据(70%)数据作为训练数据,余下的作为测试数据,此外还有交叉验证法,自助法用来评估分类模型。
-
分类学习-评价标准
-
精确率
-
精确率是针对我们预测结果而言的,(以二分类为例)它表示的是预测为正的样本中有多少是真正的正样本。那么预测为正就有两种可能了,一种就是把正类预测为正类(TP),另一种就是把负类预测为正类(FP),也就是

-
-
召回率
-
是针对我们原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。那也有两种可能,一种是把原来的正类预测成正类(TP),另一种就是把原来的正类预测为负类(FN),也就是

-
-
假设我们手上有60个正样本,40个负样本,我们要找出所有的正样本,分类算法查找出50个,其中只有40个是真正的正样本,TP: 将正类预测为正类数 40;FN: 将正类预测为负类数 20;FP: 将负类预测为正类数 10;TN: 将负类预测为负类数 30
-
-
Sklearn vs. 分类
- 与聚类算法被统一封装在sklearn.cluster
模块不同,sklearn库中的分类算法并未被统一
封装在一个子模块中,因此对分类算法的import
方式各有不同。 - Sklearn提供的分类函数包括
- k近邻(knn)
- 朴素贝叶斯(naivebayes)
- 支持向量机(svm)
- 决策树 (decision tree)
- 神经网络模型(Neural networks)等
- 这其中有线性分类器,也有非线性分类器
- 与聚类算法被统一封装在sklearn.cluster
(3)回归
- Sklearn vs. 回归
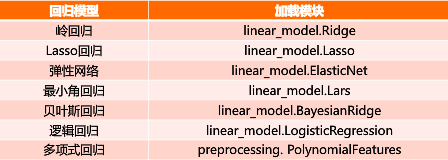
- Sklearn提供的回归函数主要被封装在两个子模块中,分别是
sklearn.linear_model和sklearn.preprocessing。 sklearn.linear_modlel封装的是一些线性函数,线性回归函数包括有- 普通线性回归函数( LinearRegression )
- 岭回归(Ridge)
- Lasso(Lasso)
- 非线性回归函数,如多项式回归(PolynomialFeatures)则通过
sklearn.preprocessing子模块进行调用
- Sklearn提供的回归函数主要被封装在两个子模块中,分别是
(4)交叉验证
- 基本思想
- 交叉验证法先将数据集D划分为k个大小相似的互斥子集,每个自己都尽可能保持数据分布的一致性,即从D中通过分层采样得到。然后,每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集;这样就可获得k组训练/测试集,从而可进行k次训练和测试,最终返回的是这个k个测试结果的均值。通常把交叉验证法称为“k者交叉验证”, k最常用的取值是10,此时称为10折交叉验证。

2.分类
(1)基本分类模型
①K近邻分类器(KNN)
-
KNN:通过计算待分类数据点,与已有数据集中的所有数据点的距离。取距离最小的前K个点,根据“少数服从多数“的原则,将这个数据点划分为出现次数最多的那个类别
-
sklearn中的K近邻分类器
- 使用
sklearn.neighbors.KNeighborsClassifier
创建一个K近邻分类器- 参数
n_neighbors:用于指定分类器中K的大小(默认值为5,注意与kmeans的区别)weights:设置选中的K个点对分类结果影响的权重(默认值为平均权重“uniform”,可以选择“distance”代表越近的点权重越高,或者传入自己编写的以距离为参数的权重计算函数)- algorithm:设置用于计算临近点的方法,因为当数据量很大的情况下计算当前点和所有点的距离再选出最近的k各点,这个计算量是很费时的,所以(选项中有ball_tree、kd_tree和brute,分别代表不同的寻找邻居的优化算法,默认值为auto,根据训练数据自动选择)
- 参数
- 使用
-
K近邻分类器的使用
-
创建一组数据 X 和它对应的标签 y
X = [[0], [1], [2], [3]] y = [0, 0, 1, 1] -
使用 import 语句导入 K 近邻分类器
from sklearn.neighbors import KNeighborsClassifier #参数 n_neighbors 设置为 3,即使用最近的3个邻居作为分类的依据,其他参数保持默认值,并将创建好的实例赋给变量 neigh neigh = KNeighborsClassifier(n_neighbors=3) #调用 fit() 函数,将训练数据 X 和 标签 y 送入分类器进行学习 neigh.fit(X, y) #调用 predict() 函数,对未知分类样本 [1.1] 分类,可以直接并将需要分类的数据构造为数组形式作为参数传入,得到分类标签作为返回值 print(neigh.predict([[1.1]])) >>>[0] #样例输出值是 0,表示K近邻分类器通过计算样本 [1.1] 与训练数据的距离,取 0,1,2 这 3 个邻居作为依据,根据“投票法”最终将样本分为类别 0
-
-
KNN的使用经验
- 在实际使用时,我们可以使用所有训练数据构成特征 X 和标签 y,使用fit() 函数进行训练。在正式分类时,通过一次性构造测试集或者一个一个输入样本的方式,得到样本对应的分类结果。有关K 的取值:
- 如果较大,相当于使用较大邻域中的训练实例进行预测,可以减小估计误差,但是距离较远的样本也会对预测起作用,导致预测错误
- 相反地,如果 K 较小,相当于使用较小的邻域进行预测,如果邻居恰好是噪声点,会导致过拟合。
- 一般情况下,K 会倾向选取较小的值,并使用交叉验证法选取最优 K 值
- 在实际使用时,我们可以使用所有训练数据构成特征 X 和标签 y,使用fit() 函数进行训练。在正式分类时,通过一次性构造测试集或者一个一个输入样本的方式,得到样本对应的分类结果。有关K 的取值:
②决策树
-
决策树是一种树形结构的分类器,通过顺序询问分类点的属性决定分类点最终的类别。通常根据特征的信息增益或其他指标,构建一颗决策树。在分类时,只需要按照决策树中的结点依次进行判断,即可得到样本所属类别
-
sklearn中的决策树
- 在sklearn库中,可以使用
sklearn.tree.DecisionTreeClassifier创建一个决策树用于分类- 参数
criterion:用于选择属性的准则,可以传入“gini”代表基尼系数,或者“entropy”代表信息增益max_features:表示在决策树结点进行分裂时,从多少个特征中选择最优特征。可以设定固定数目、百分比或其他标准。它的默认值是使用所有特征个数
- 参数
- 在sklearn库中,可以使用
-
决策树的使用
#首先,我们导入 sklearn 内嵌的鸢尾花数据集 from sklearn.datasets import load_iris #接下来,我们使用 import 语句导入决策树分类器,同时导入计算交叉验证值的函数 cross_val_score from sklearn.tree import DecisionTreeClassifier from sklearn.model_selection import cross_val_score #我们使用默认参数,创建一颗基于基尼系数的决策树,并将该决策树分类器赋值给变量 clf clf = DecisionTreeClassifier() #将鸢尾花数据赋值给变量 iris iris = load_iris() #这里我们将决策树分类器做为待评估的模型,iris.data鸢尾花数据做为特征,iris.target鸢尾花分类标签做为目标结果,通过设定cv为10,使用10折交叉验证。得到最终的交叉验证得分 cross_val_score(clf, iris.data, iris.target, cv=10) >>> array([ 1. , 0.93..., 0.86..., 0.93..., 0.93..., 0.93..., 0.93..., 1. , 0.93..., 1. ]) #以仿照之前 K近邻分类器的使用方法,利用 fit() 函数训练模型并使用predict() 函数预测 clf.fit(X,y) clf.predict(x) -
决策树本质上是寻找一种对特征空间上的划分,旨在构建一个训练数据拟合的好,并且复杂度小的决策树
-
在实际使用中,需要根据数据情况,调整DecisionTreeClassifier类中传入的参数,比如选择合适的criterion,设置随机变量等。
③朴素贝叶斯
-
朴素贝叶斯分类器是一个以贝叶斯定理为基础的多分类的分类器
-
对于给定数据,首先基于特征的条件独立性假设,学习输入输出的联合概率分布,然后基于此模型,对给定的输入x,利用贝叶斯定理求出后验概率最大的输出y。
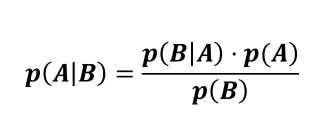
-
sklearn中的朴素贝叶斯
- 在sklearn库中,实现了三个朴素贝叶斯分类器,如下表所示

- 区别在于假设某一特征的所有属于某个类别的观测值符合特定分布,如,分类问题的特征包括人的身高,身高符合高斯分布,这类问题适合高斯朴素贝叶斯
- 在sklearn库中,可以使用
sklearn.naive_bayes.GaussianNB创建一个高斯朴素贝叶斯分类器,其参数有:- priors :给定各个类别的先验概率。如果为空,则按训练数据的实际情况进行统计;如果给定先验概率,则在训练过程中不能更改。
- 在sklearn库中,实现了三个朴素贝叶斯分类器,如下表所示
-
朴素贝叶斯的使用
#导入 numpy 库,并构造训练数据 X 和 y import numpy as np X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]]) Y = np.array([1, 1, 1, 2, 2, 2]) #使用 import 语句导入朴素贝叶斯分类器 from sklearn.native_bayes import GaussianNB #使用默认参数,创建一个高斯朴素贝叶斯分类器,并将该分类器赋给变量clf clf.GaussianNB(priors=None) #类似的,使用 fit() 函数进行训练,并使用 predict() 函数进行预测,得到预测结果为 1。(测试时可以构造二维数组达到同时预测多个样本的目的) clf.fit(X, Y) print(clf.predict([[-0.8, -1]])) >>> [1]- 朴素贝叶斯是典型的生成学习方法,由训练数据学习联合概率分布,并求得后验概率分布。
- 朴素贝叶斯一般在小规模数据上的表现很好,适合进行多分类任务




 浙公网安备 33010602011771号
浙公网安备 33010602011771号