[Atcoder] ARC135

A - Floor, Ceil - Decomposition

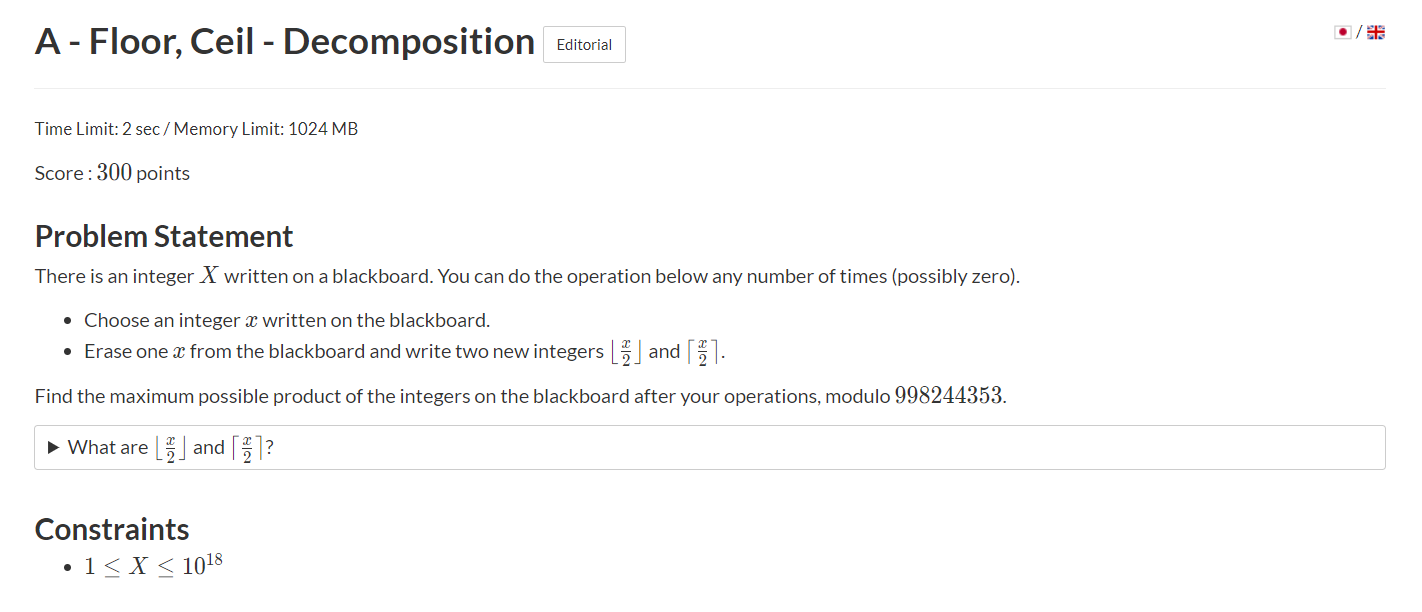
题意

给出一个数x，这个数可以分解为x/2上取整，和x/2下取整，然后可以继续分解，求分解完后能组成的最大值

思路

对于一个x，范围是1 ~ 1e18，如果一直分解肯定会超时。因为每次都是缩小，所以可以将每次分解后的数记录下来，然后一次性分解。用map来记录每个数出现的次数，queue来存当前要分解的数，当只剩2或者3的时候，所有的2和3相乘即可。因为2和3可能很大，所以要用到快速幂

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 998244353;
ll qmi(ll m, ll k, ll p) {
	ll res = 1 % p, t = m;
	while(k) {
		if(k & 1) res = res * t % p;
		t = t * t % p;
		k >>= 1;
	}
	return res;
}
map<ll, ll> mp;
queue<ll> q;
int main(){
	ll x;
	cin >> x;
	q.push(x);
	mp[x] = 1;
	ll ans = 1;
	while(!q.empty()) {
		ll a = q.front();
		ll b = mp[a];
		mp[a] = 0;
		q.pop();
		if(a <= 4) {
			ans = ans * qmi(a, b, mod) % mod;
		}
		else {
			ll a1 = a / 2, a2 = a / 2 + a % 2;
			if(!mp[a1]) q.push(a1);
			if(!mp[a2]) q.push(a2);
			mp[a1] += b;
			mp[a2] += b;
		}
	}
	cout << ans % mod << endl;
	
	
	return 0;
}

B - Sum of Three Terms

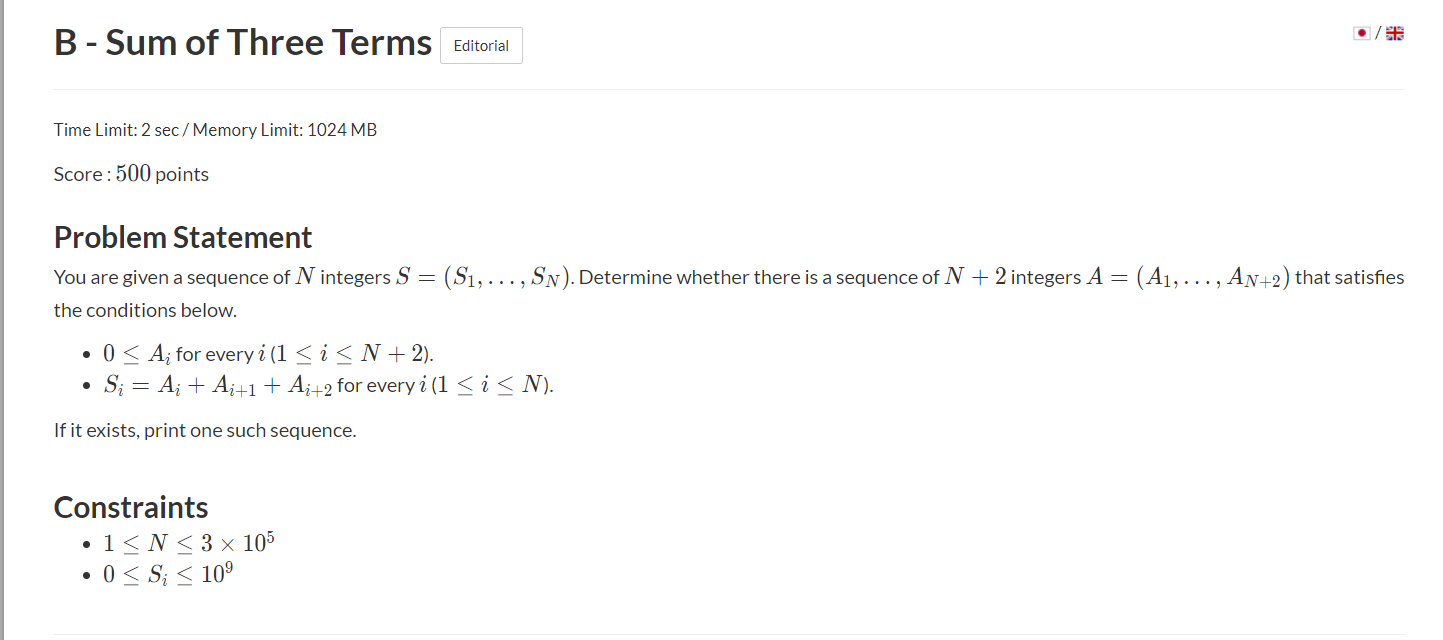
思路

这题的式子等哪天有空再重新推一下吧。。。没推明白感觉，后面条件也没搞明白
只能先用一下官方题解的图

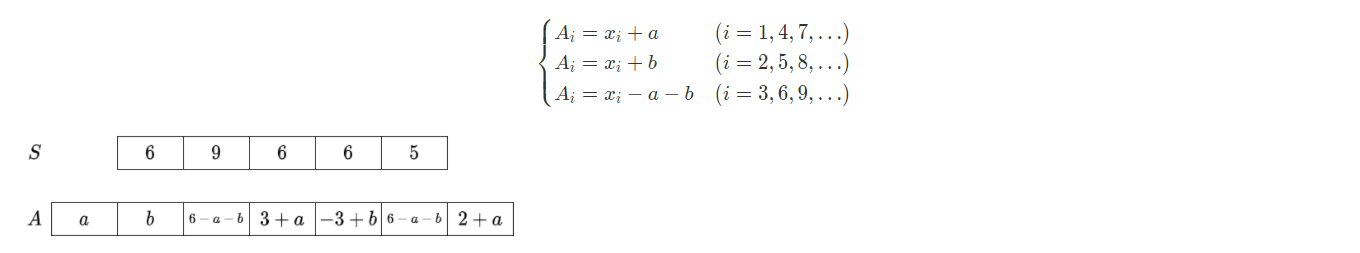
最主要的是要将A1和A2设为变量a和b，因为确定这两个数后，可以推出整个A数组
将a和b代入后会发现，当i % 3 == 1的时候，都是+a，当i % 3 == 2的时候都是+b，当i % 3 == 0的时候，都是-a-b。
为了使A成立，要满足以下几个条件

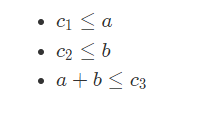
当c1 + c2 <= c3的时候a和b就是c1和c2，否则无解

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 3e5 + 10;
ll a[N], s[N];
int main(){
	int n;
	cin >> n;
	for(int i = 1; i <= n; i ++) {
		cin >> s[i];
	}
	bool flag = false;
	ll sum = 0;
	ll c1 = 0, c2 = 0, c3 = 0;
	for(int i = 1; i < n; i += 3) {
		sum += s[i] - s[i + 1];
		c1 = max(c1, sum);
	}
	sum = 0;
	for(int i = 2; i < n; i += 3) {
		sum += s[i] - s[i + 1];
		c2 = max(c2, sum);
	}
	sum = 0;
	for(int i = 3; i < n; i += 3) {
		sum += s[i] - s[i + 1];
		c3 = max(c3, sum);
	}
	if(c1 + c2 + c3 > s[1]) {
		cout << "No" << endl;
	}
	else {
		cout << "Yes" << endl;
		a[1] = c1, a[2] = c2, a[3] = s[1] - c1 - c2;
		for(int i = 2; i <= n; i ++) {
			a[i + 2] = s[i] - a[i] - a[i + 1];
		}
		for(int i = 1; i <= n + 2; i ++) {
			cout << a[i] << " ";
		}
		cout << endl;
	}
	
	return 0;
}

C - XOR to All

题意

给出一个序列A，选择一个数与整个序列进行异或，求任意次操作后，序列和能到达的最大值

思路

先选择An，A1 = A1 xor An, An - 1 = An - 1 xor An, An = An xor An = 0
再选择An-1，A1 = A1 xor An xor An-1 xor An = A1 xor An-1
结合异或的规律，会发现每个数xor后再进行xor，与上一轮操作没有影响
所以直接枚举每一个Ai即可
因为是异或，计算时找到与当前位相反的数量乘当前位的权值，加到ans里

代码

#include<bits/stdc++.h>
using namespace std;
const int N = 3e5 + 10;
typedef long long ll;
ll a[N];
int cnt1[50], cnt0[50];
int main(){
	int n;
	cin >> n;
	int w = 0;
	ll ans = 0;
	for(int i = 1; i <= n; i ++) {
		cin >> a[i];
		ans += a[i];
		int k = 1;
		ll p = a[i];
		while(k <= 31) {
			if(p & 1) {
				cnt1[k ++] ++;
			}
			else {
				cnt0[k ++] ++;
			}
			if(p) p >>= 1;
		}
	}
	
	for(int i = 1; i <= n; i ++) {
		ll res = 0;
		ll p = a[i];
		int k = 1;
		ll nice = 1;
		//cout << w << endl;
		while(k <= 31) {
			if(p & 1) {
				res += cnt0[k] * nice;
			}
			else {
				res += cnt1[k] * nice;
			}
			nice *= 2;
			if(p) p >>= 1;
			k ++;
			//cout << res << endl;
		}
		//cout << res << endl;
		ans = max(ans, res);
	}
	cout << ans << endl;
	
	return 0;
}