[Acwing246]区间最大公约数

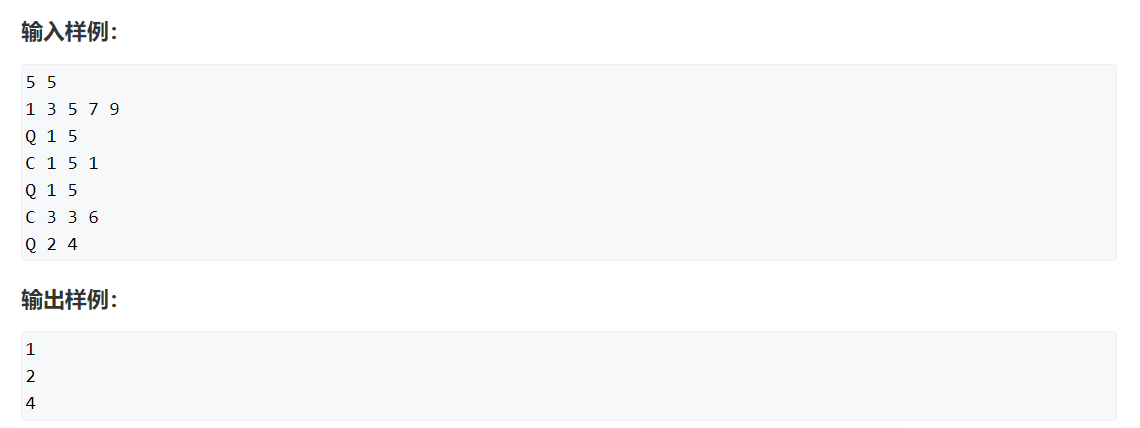
一、题目

Acwing246

二、思路

通过线段树来维护，因为题目需要达成区间增加d，一个数的最大公约数就是它本身，同时(a, b, c)的最大公约数与(a, b - a, c - b)的最大公约数相等，所以可以通过维护一个差分序列来写，将区间修改改为单点修改。在询问区间x到y的最大公约数时，只需要求出x的前缀和为a，x + 1到y的最大公约数，再对这两个求一个最大公约数即可

三、代码

#include<bits/stdc++.h>
using namespace std;
#define u1 (u << 1)
#define u2 (u << 1 | 1)
const int N = 5e5 + 10;
typedef long long ll;
struct Node {
	int l, r;
	ll sum, d;
}tr[4 * N];
ll a[N], b[N];

ll gcd(ll a, ll b){
	return b ? gcd(b, a % b) : a;
}
void pushup(Node &u, Node &l, Node &r){
	u.sum = l.sum + r.sum;
	u.d = gcd(l.d, r.d);
}
void pushup(int u){
	pushup(tr[u], tr[u1], tr[u2]);
}

void build(int u, int l, int r){
	//printf("tree: %d %d %d\n", u, l, r);
	if(l == r) {
		tr[u] = {l, r, b[l], b[l]};
	}
	else {
		tr[u].l = l, tr[u].r = r;
		int mid = l + r >> 1;
		build(u1, l, mid), build(u2, mid + 1, r);
		pushup(u);
	}
	
}

void modify(int u, int x, ll v){
	if(tr[u].l == x && tr[u].r == x){
		 ll y = tr[u].sum + v; //注意是+v
		 tr[u] = {x, x, y, y};
	}
	else {
		int mid = tr[u].l + tr[u].r >> 1;
		if(x <= mid) modify(u1, x, v);
		else modify(u2, x, v);
		pushup(u);
	}
}

Node query(int u, int l, int r){
	if(tr[u].l >= l && tr[u].r <= r) return tr[u];
	int mid = tr[u].l + tr[u].r >> 1;
	if(r <= mid) return query(u1, l, r);
	else if(l > mid) return query(u2, l, r);
	else {
		auto left = query(u1, l, r), right = query(u2, l, r);
		Node res;
		pushup(res, left, right);
		return res;
	}
}
int main(){
	int n, m;
	cin >> n >> m;
	for(int i = 1; i <= n; i ++){
		cin >> a[i];
		b[i] = a[i] - a[i - 1];
	}
	build(1, 1, n);
	char op[2];
	int x, y;
	ll p;
	while(m --){
		cin >> op;
		cin >> x >> y;
		if(*op == 'C') {
			cin >> p;
			modify(1, x, p);
			if(y + 1 <= n) modify(1, y + 1, -p);//这里要注意只有在y + 1 <= n时才能修改y + 1号点，不然会越界
		}
		else {
			auto left = query(1, 1, x), right = query(1, x + 1, y);
			printf("%lld\n", abs(gcd(left.sum, right.d)));
		}
	}
	
	return 0;
}