[NC14694]栗酱的数列

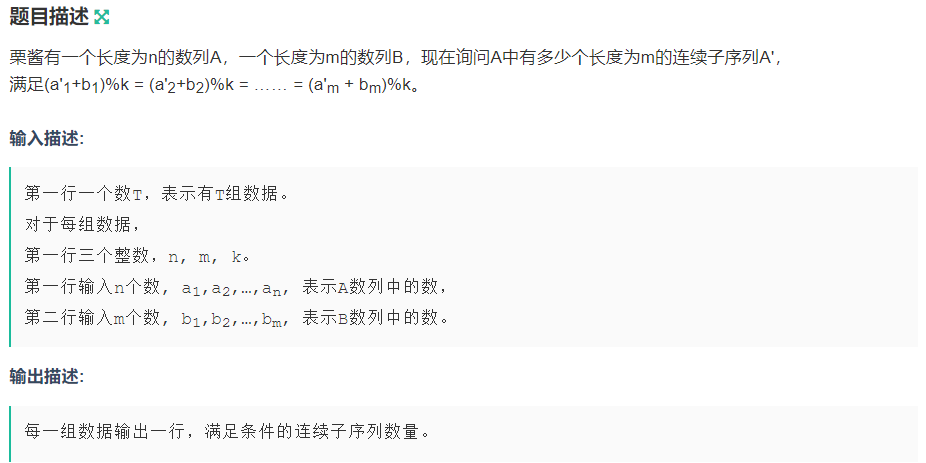
一、题目

NC14694

二、思路

直接用题目的条件来判断的话，只能想到用暴力，但是暴力必然超时，所以可以从题目的条件式子入手，将(a'1+b1)%k = (a'2+b2)%k改写成(a'1 + b1 - a'2 - b2) % k = 0
因为右边为0是个定值，这样的话就可以用kmp算法来进行匹配

三、代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 200010;
int a[N], b[N], sumb;
int k, ne[N], s[N], t[N];	
int T;
int n, m;

void getne(){
	ne[1] = 0;
	int i = 1, j = 0;
	while(i < m){ //这里只用1 ~ m-1即可，因为只有最多只有m - 1个子序列 
		if(j == 0 || t[i] == t[j]){ //当前子串的j还没开始取或者相等的时候 
			i ++;
			j ++;
			ne[i] = j;
		}
		else j = ne[j]; //往前退一个 
	}
}

int kmp(){
	int ans = 0;
	getne();
	int i = 1, j = 1;
	while(i < n){
		if(j == 0 || (s[i] + t[j]) % k == 0){ //这里将kmp匹配成功的条件改成我们的条件式 
			i ++;
			j ++;
		}
		else j = ne[j];
		if(j == m) ans ++, j = ne[j];
	}
	return ans;
}

int main(){
	cin >> T;
	while(T --){
		sumb = 0;
		cin >> n >> m >> k;
		for(int i = 1; i <= n; i ++){
			cin >> a[i];
			a[i] %= k; //这里注意先%一下，或者放后面再%也可以 
		}
		for(int i = 1; i <= n - 1; i ++){
			s[i] = ((a[i] - a[i + 1]) + k) % k; //这里要注意被模数是负数的情况，+k再%统一取法 
		}
		for(int i = 1; i <= m; i ++){
			cin >> b[i];
			b[i] %= k;
		}
		for(int i = 1; i <= m; i ++){
			t[i] = ((b[i] - b[i + 1]) + k) % k;  
		}
		printf("%d\n", kmp());
	}

	return 0;
}

四、结尾

写这题的时候才发现自己对kmp算法掌握的还不是很透彻，也没有第一时间想到这题可以通过kmp算法来写，第二个问题是对取模运算中的+k%k这里有点没搞明白，回头再巩固一下kmp算法吧