[NC14294]Butterfly

一、前言

这题我写的真的一言难尽，debug了一天才调出来，还是太菜了。从最开始的题意问题，没理解透题意，漏了一个左上顶点到左下顶点、右上顶点到右下顶点之间都要为X的条件，再到后来折磨了我一天的问题，就是按我的思路来想，在这种情况下

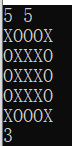
我原先的思路输出的是1，因为只判断了外面一圈，里面就没判断了，后来改了之后发现超时了，虽然现在还不明白为什么超时，之后就重新改了下思路，按照枚举每个左上顶点，然后判断有没有能和他组成蝴蝶形状的右上顶点。总的来说，debug能力还是不够，以后继续加油吧！

二、题目

NC14294

三、思路

首先不难想到的就是暴力做法
暴力：对每一个点判断他的左上、左下、右上、右下四个点以及下方的点是否和它本身是同一个符号
如果是，则继续判断，不是则结束，记录max；
T：2000 * 2000 * 5000
K：2000 * 2000

然后就想到用dp优化，因为对角线上每个点的状态都可以通过前一个点来得出，这样就减少循环次数
DP：对于当前位置，由前一个方向的连续的符号数量转移而来
dp[2000][2000][6]
dp[i][j][k]
dp数组表示i, j位置下k方向上该符号的数量；
我这里跑了两遍for循环，一次是从上到下，一次从下到上，在从下到上的时候顺便记录当前位置的下方有多少个连续的X，这样就能把每个点的四个方向以及下方的X数量记录下来
然后再枚举每一个点作为左上顶点，将该点下方X的数量与右下方X的数量较小的那个拿来作为对角线的长度，然后从该行的j + 1 ~ j + d - 1的范围里找能组成蝴蝶形状的最大的右上顶点并更新maxn
T：2000 * 2000 * 500；
K：2000 * 2000 * 6；
初始化：dp全为0

四、代码

#include<bits/stdc++.h>
using namespace std;
int dp[2010][2010][6];
char mp[2010][2010];
int dir[4][2] = {{1, 1}, {-1, -1}, {1, -1}, {-1, 1}};
bool flag[5];
bool fl, fl2;
int main(){
    int n, m;
    cin >> n >> m;
    memset(mp, '*', sizeof mp);
    for(int i = 1; i <= n; i ++){
        scanf("%s", mp[i] + 1);
    }
    int maxn = 0;
    int minn = 1e9;
    for(int i = 1; i <= n; i ++){
        for(int j = 1; j <= m; j ++){
            if(mp[i][j] == 'X') fl2 = true; //这里判断是否出现过X，因为单个X也是蝴蝶形状，结果最小为1 
            for(int k = 0; k < 4; k ++){
                if(mp[i][j] == mp[i + dir[k][0]][j + dir[k][1]] && mp[i][j] == 'X'){
                    dp[i][j][k] = dp[i + dir[k][0]][j + dir[k][1]][k] + 1; //这里记录该点左上和右上有多少个连续的X 
                }
            }
        }
    }
    for(int i = n; i >= 1; i --){
        for(int j = 1; j <= m; j ++){
        	if(mp[i][j] == 'X') dp[i][j][5] = dp[i + 1][j][5] + 1; //这里记录该点下方有多少个连续的X 
            for(int k = 0; k < 4; k ++){
                if(mp[i][j] == mp[i + dir[k][0]][j + dir[k][1]] && mp[i][j] == 'X'){
                    dp[i][j][k] = dp[i + dir[k][0]][j + dir[k][1]][k] + 1; //这里记录该点左下和右下有多少个连续的X 
                }
            }
        }
    }
    for(int i = 1; i <= n; i ++){
        for(int j = 1; j <= m; j ++){
            minn = 1e9;
            fl = false;
			minn = min(dp[i][j][5], dp[i][j][0] + 1); //取最小值作为对角线的长度 
			if(minn % 2 == 0) minn --; //因为要有中心点，所以对角线长度必须为奇数 
			while(minn && maxn < minn){ //剪枝了一下，如果maxn大于minn了就不需要继续，直接退出 
				if(dp[i][j + minn - 1][5] >= minn && dp[i][j + minn - 1][2] + 1 >= minn){ //判断右上顶点是否满足条件 
					maxn = max(maxn, minn);
				}
				minn = minn - 2;
			}
        }
    }
    if(maxn == 0 && fl2) cout << 1 << endl; //特判单个X的蝴蝶形状的情况 
    else cout << maxn << endl;
     
    return 0;
}