1.时空复杂度
1.1 函数渐进增长率
① 定义:给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有的 n>N,f(n)总是比g(n)大,那么我们说f(n)的增长渐进快于g(n)。
② 判断一个算法的效率时,函数中的常数和其他次要项一般忽略不计,关注最高阶项。
1.2 时间复杂度
① 时间复杂度:运行时间的需求;T(n) = O(f(n))
② 常数阶 O(1)
线性阶 O(n)
对数阶 O(logn) :一定要注意掌握计算方法
nlogn阶 O(nlogn)
平方阶 O(n2)
立方阶 O(n3)
指数阶 O(2n)
③ 常见时间复杂度排序:
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)
④ 最坏情况 与 平均情况
最坏情况:运行次数最大需要,查找完所有单元;
平均情况:要查找的任意一个单元中的概率是一样的;
1.3 空间复杂度
①定义:通过计算算法所需的存储空间实现;S(n) = O(f(n))
1.4 求解时间复杂度
① master定理
a>=1,b>1为常数,设f(n)为一函数,T(n)由递归式T(n)=aT(n/b)+f(n)。
那么,T(n)(为非负整数)可能有如下渐进界。
(1)
![]()
(2)
![]()
(3)

② 例子
(1)
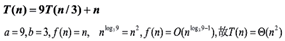
(2)
![]()
(3)
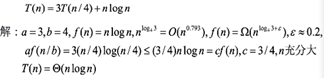



 浙公网安备 33010602011771号
浙公网安备 33010602011771号