【知识强化】第二章 数据的表示和运算 2.4 算术逻辑单元ALU
从本节开始我们就进入到本章的最后一节内容了,也就是我们算术逻辑单元的它的实现。这部分呢是数字电路的一些知识,所以呢,如果你没有学过数字电路的话,也不要慌张,我会从基础开始给大家补起。那么在计算机当中,运算器承担了执行各种算术和逻辑运算的工作,那么运算器是由什么组成的呢?我们之前也讲过,在第一章的时候。运算器是由算术逻辑单元,累加器,状态寄存器和通用寄存器组成的。所以,运算器当中,最重要的一部分就是我们的算术逻辑单元。所以我们将要讲解算术逻辑单元它的实现原理。

那么我将从这两个方面给大家讲起。首先呢是ALU,也就是我们的算术逻辑单元。它的功能是什么,然后根据它的功能我们来实现它的基本结构。那么在ALU当中呢,最重要的还是我们的加法器。所以我们将要在第二讲给大家讲一下加法器是如何实现的。那么我们先进入第一节的内容,就是ALU它的功能和基本结构。

那么算术逻辑单元我们之前就讲过了,运算器当中最重要的一部分就是算术逻辑单元。但它为什么叫做算术逻辑单元呢?很显然它是实现了算术和逻辑运算这个工作。那么也就是从名字来看,这个算术和逻辑单元(Arithmetic and Logic Unit) 。那么什么是算术运算呢?就是我们的四则运算加减乘除这些。那么什么叫逻辑运算呢?就是与或非异或这些就是逻辑运算。那么还要一些辅助的功能,比如像移位啊求补啊它也能进行一些操作。

那么这就是一个简单的算术逻辑单元的一个概念图。

首先,它接收了两个操作数,也就是Ai和Bi,也就是一个输入信号。其实呢你光知道输入信号没有用,你还要知道我们要用这个算术逻辑单元(Arithmetic and Logic Unit)干什么,对它进行一个什么样的操作。
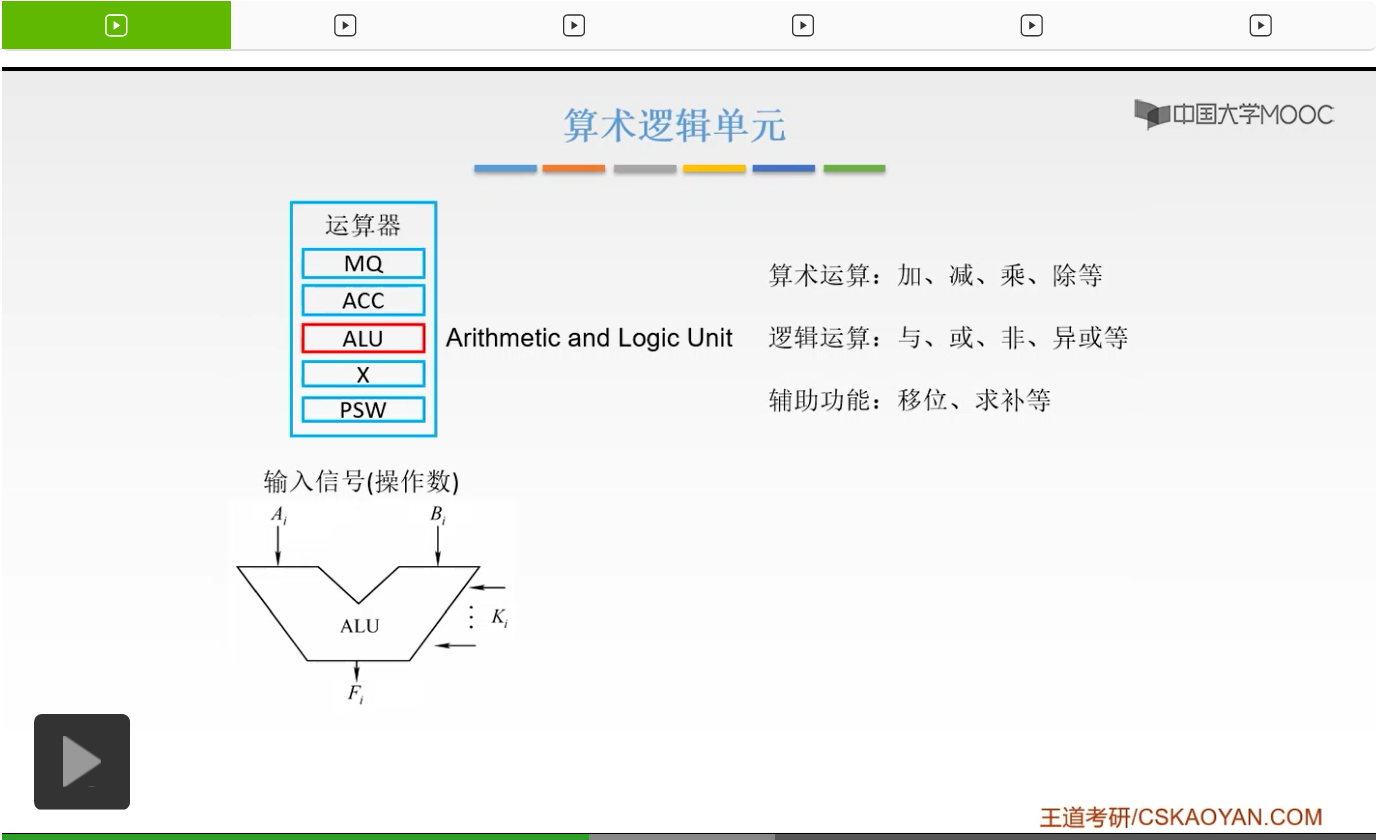
所以呢就要有一个控制信号Ki,它是由我们的指令译码产生的一个控制信号。

有了输入信号有了控制信号,那么我们就用这个控制信号来对操作数执行一个运算,然后产生我们的运算结果,也就是我们的输出信号。那么这就是我们算术逻辑单元要实现的一个功能,就是接收一个输入信号,然后再接收一个控制信号,然后根据控制信号所给控制信息我们对输入信号进行一个操作,然后操作完成之后产生一个运算结果也就是一个输出信号。
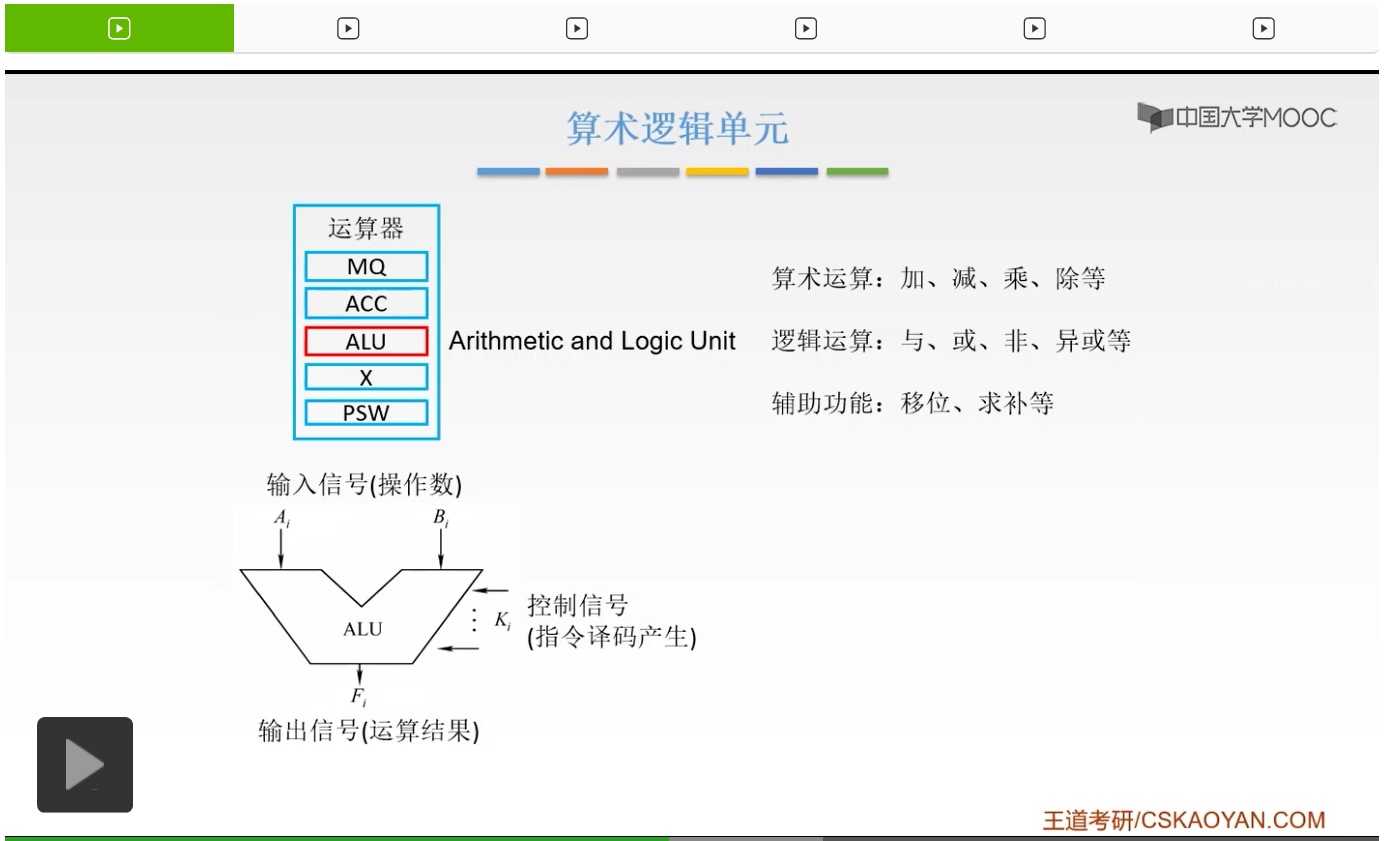
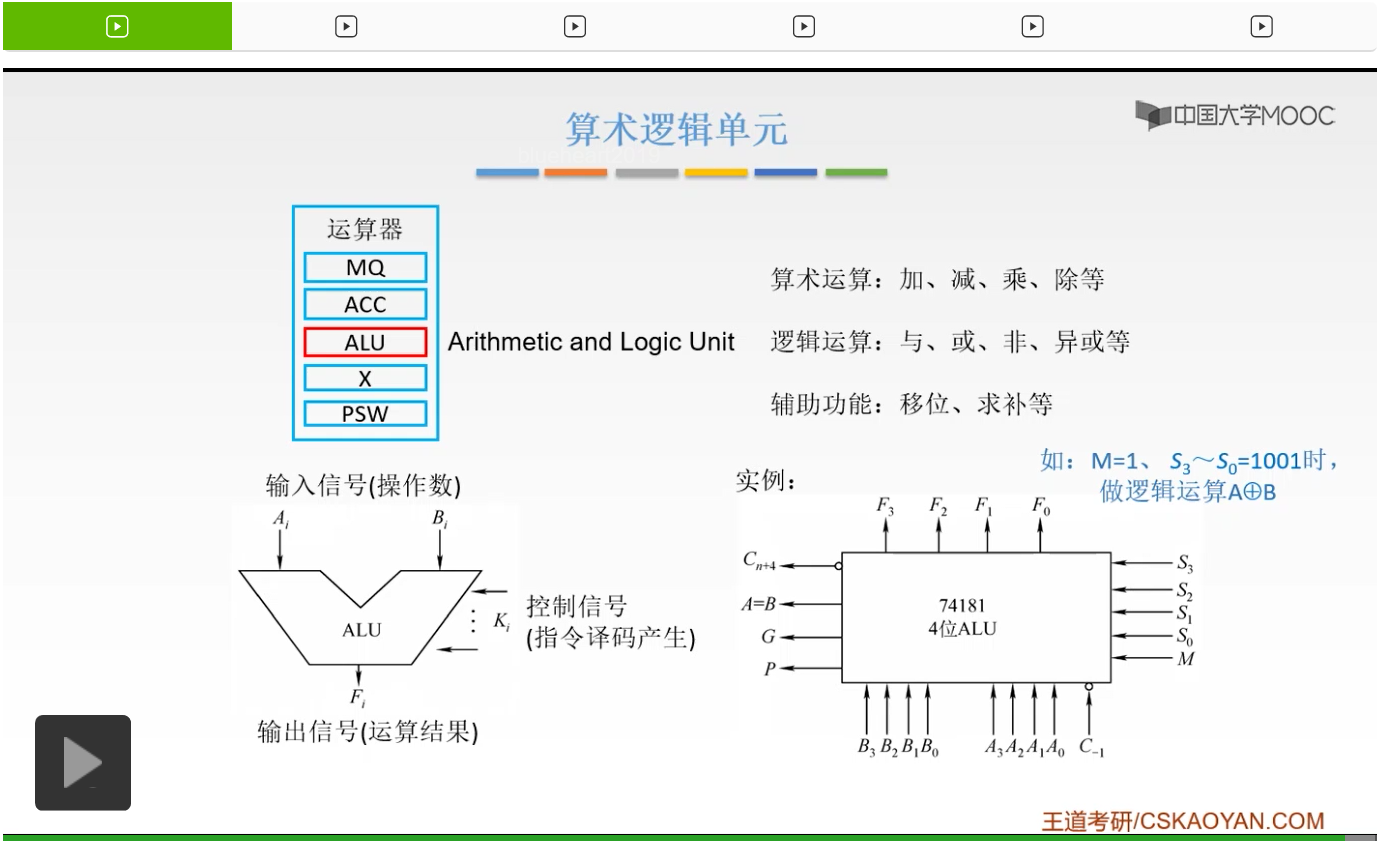
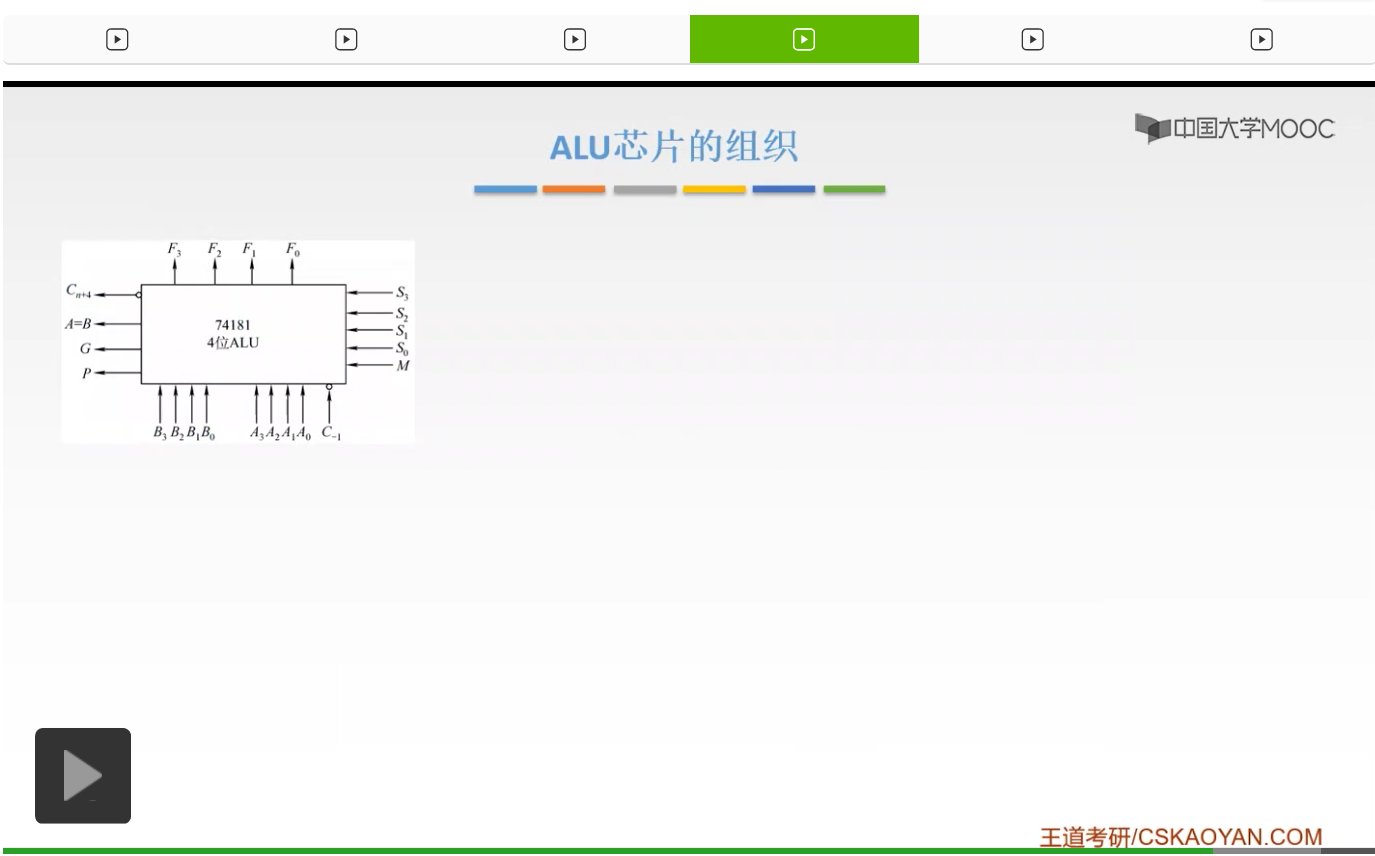
这是一个概念图,我们来看一个具体的实例。这是一个具体的芯片74181,这个74181呢是它的编号,它是一个四位的ALU。那么什么叫四位的ALU呢?它可以执行四位的运算。也就是说我们的B3B2B1B0是一个四位的二进制数,然后A3A2A1A0呢,它也是一个四位的二进制数。然后有了这两个输入信号,我们还接收S3S2S1S0和M,这5个就是我们的控制信号。
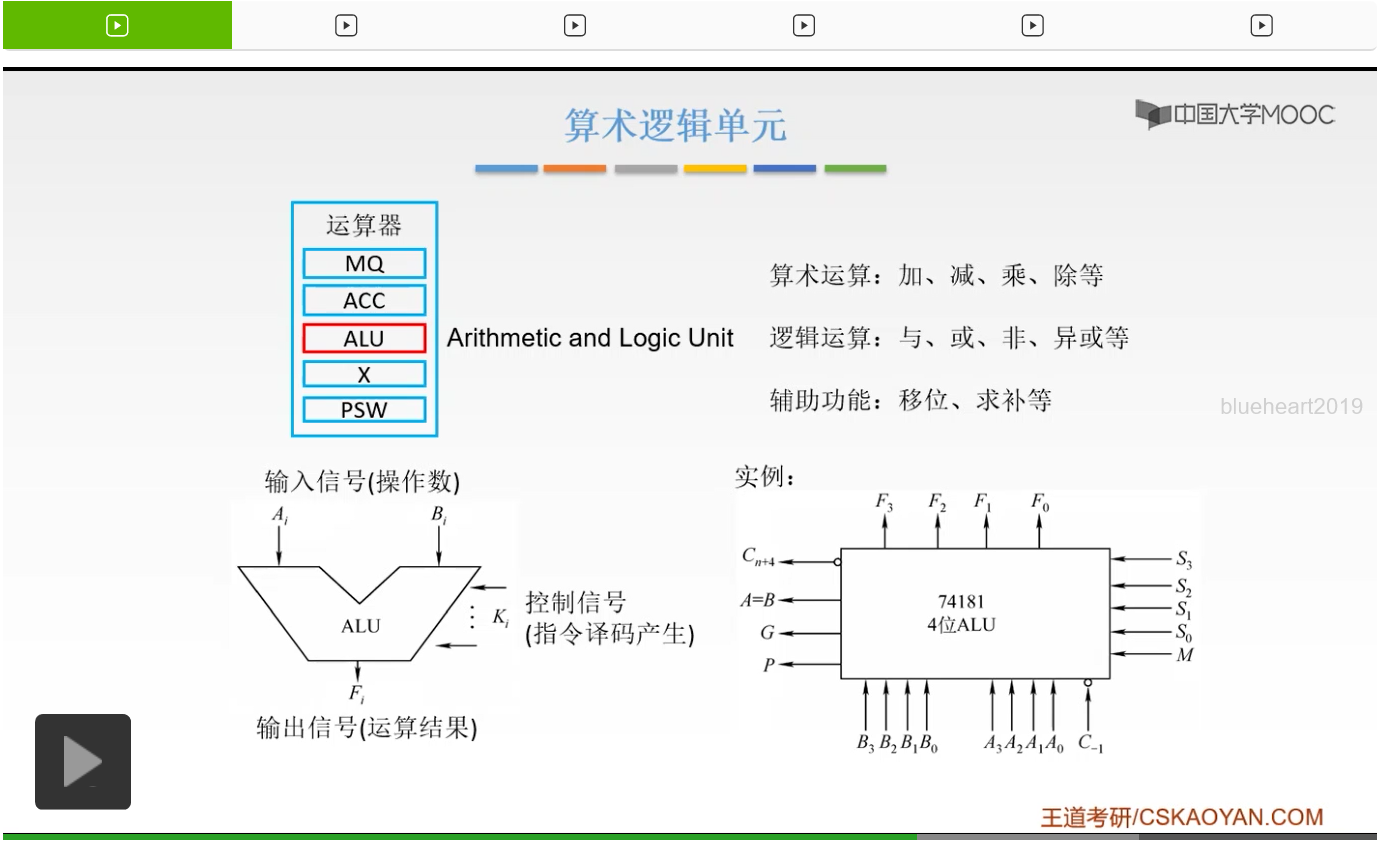
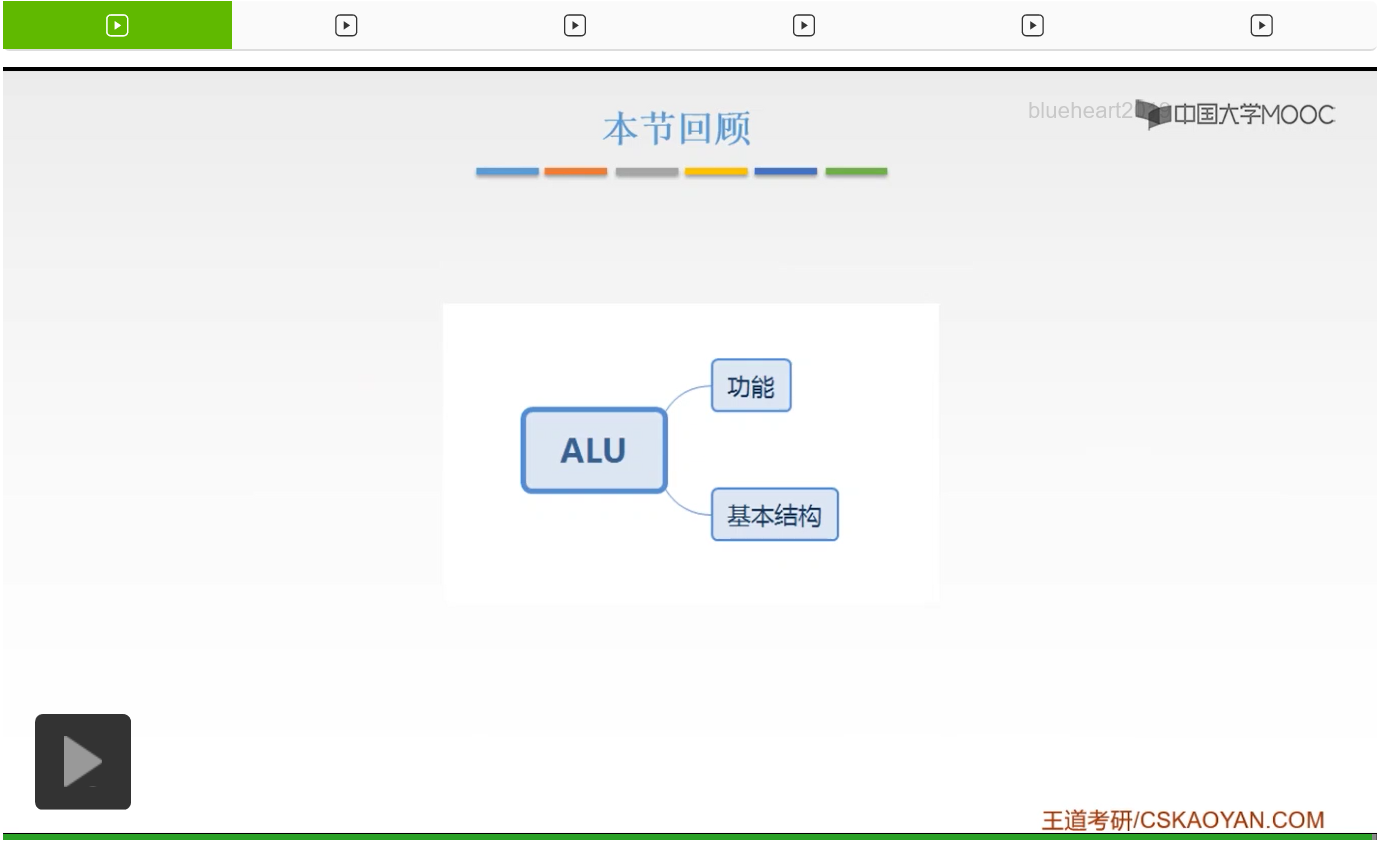
比如说M=1的时候,我就知道我要做的操作呢是一个逻辑操作,也就是逻辑运算。然后S3S2S1S0分别是1001,这时候它做的是什么逻辑操作呢?就是一个异或的一个运算。所以呢我们就知道我们要用这个ALU进行的是一个异或运算,把B3B2B1B0和A3A2A1A0进行一个异或,然后产生F3F2F1F0,就是我们的输出信号,也就是我们的运算结果。同时呢,左边还有一些东西呢,是用来级联的时候。也就是说,如果现在有两个ALU把它连在一起,我将要给它输出的一个东西,这个在后面我们将要看一下。好,这就是我们的算术逻辑单元它的功能以及它的一个基本结构,大家应该都掌握清楚了。好的,我们再来回顾一下,我们的算术逻辑单元呢它是运算器当中的核心部件,从它的名字就可以知道它是进行算术运算和逻辑运算的。那么它的功能就是进行算术运算、逻辑运算还有一些辅助功能。然后呢它是接收两个操作数,也不一定是两个,但是一般情况下是接收两个操作数,也就是我们的输入信号。然后再接收一个控制信号,用控制信号所给的控制信息对我们的操作数进行一个运算,然后产生一个结果,也就是输出信号。这就是我们算术逻辑单元的基本的功能和它的一个基本的结构。
那么我们本节就讲完了,就是讲解了ALU它的功能和基本结构。
考虑到有一些同学可能没有学过数字电路,那么在此之前我将要给大家补充一下关于数字电路的一些知识。如果你学习过数字电路,你可以复习一下,也可以跳过本节的内容,直接进入下一讲内容。因为在本节的内容只是一个补充,在书上呢也是没有的。
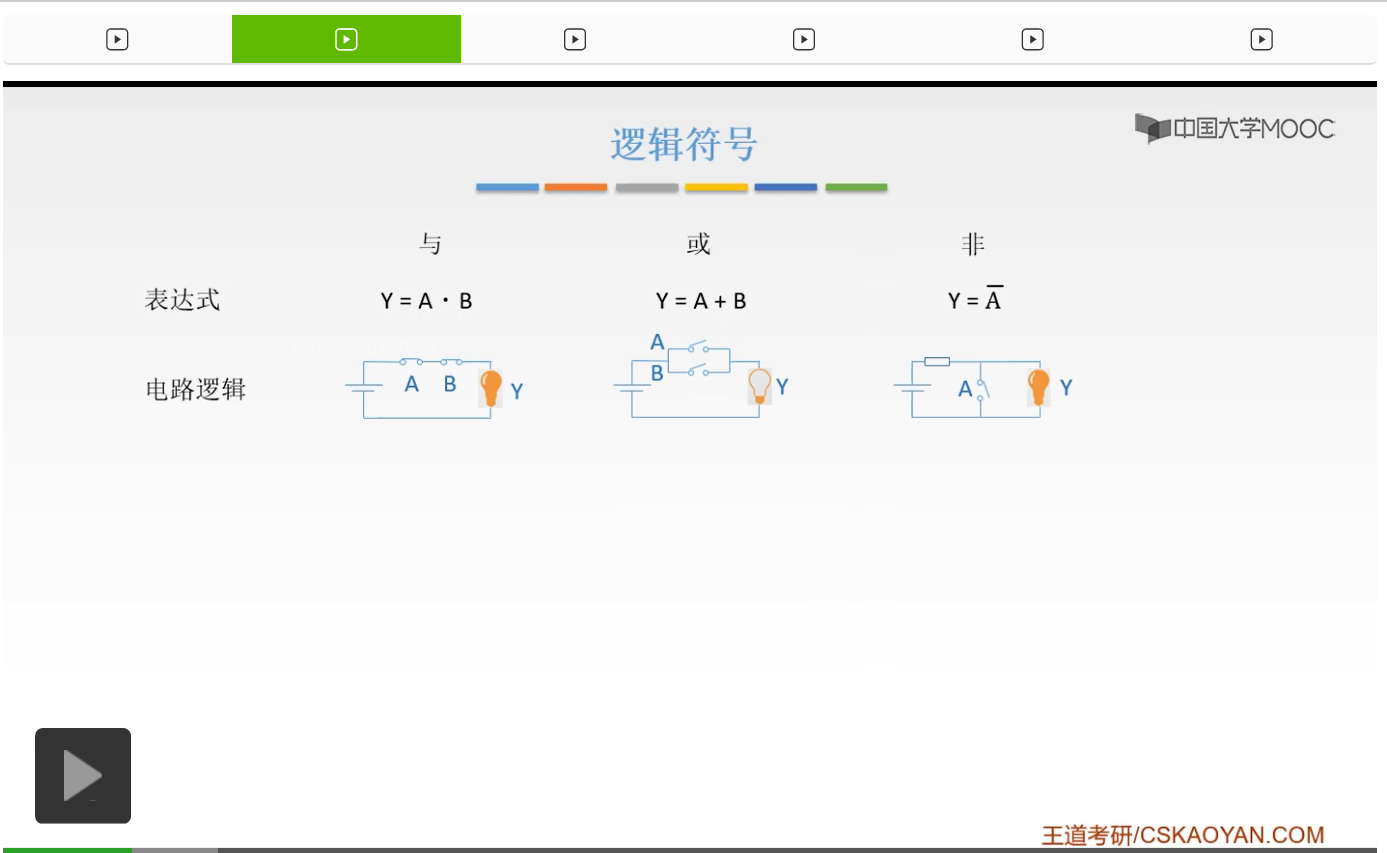
好的,那么数字电路当中,首先最基础的就是我们的逻辑运算。我们首先要讲一下,基础的逻辑运算、逻辑符号。那么首先我们已经知道了与或非是我们最基本的三种运算,那么什么是与呢?我们可以用电路来形象地描述它。它是一个串联电路,只有当A和B同时闭合的时候我们的灯泡才会亮。光是A闭合,光是B闭合,都是没有用的。

只有当A和B同时闭合的时候我们的灯泡才会亮。那么这就是与运算的一个逻辑。
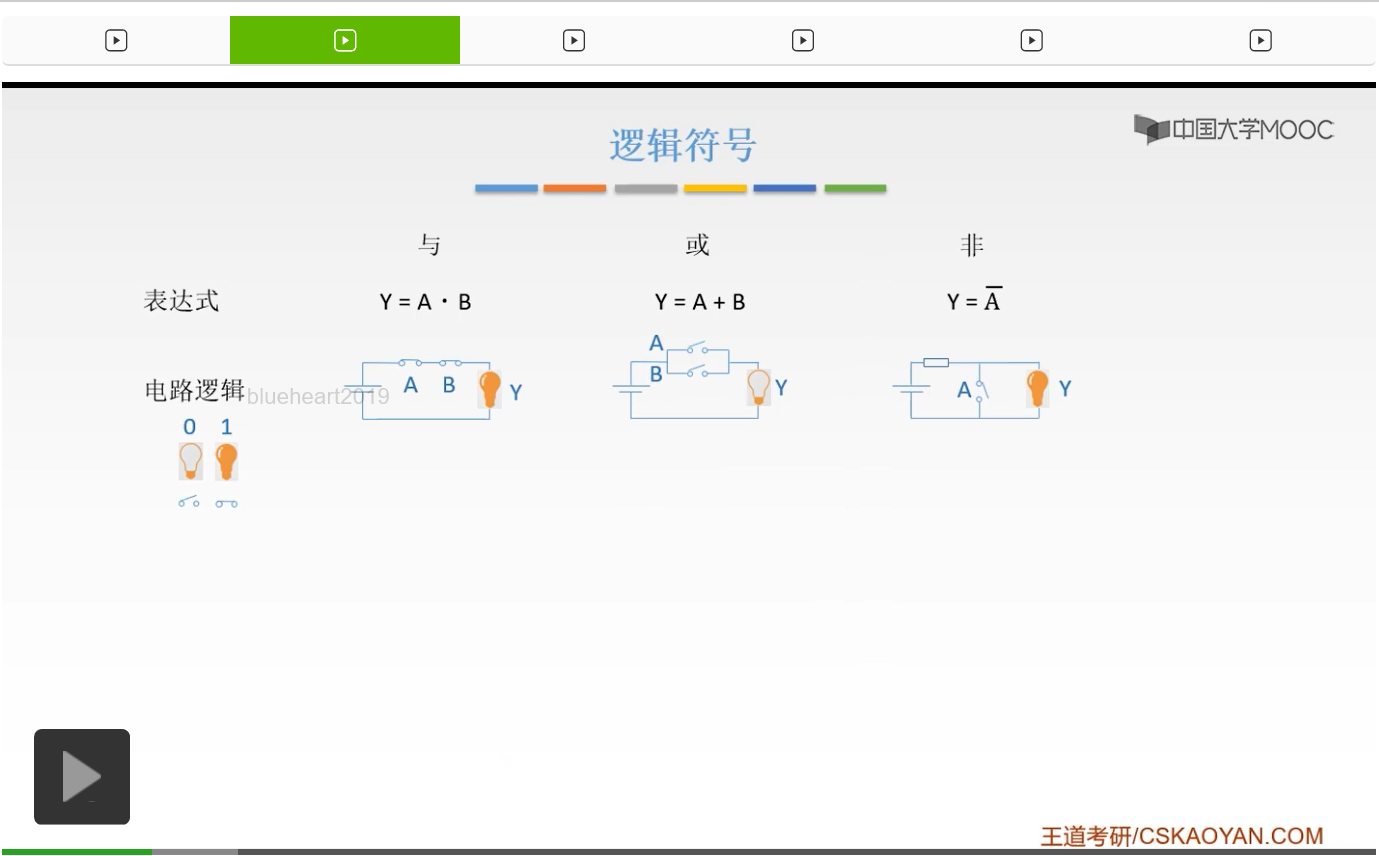
我们可以把灯泡亮看成是1,把灯泡不亮看成是0。把开关断开看成是0,把开关闭合看成是1。
由此我们可以得到这样的一张表叫做真值表。那么什么是真值表呢?也就是给出A、B,也就是给出它的输入,我们给出一个输出给出Y。当A、B同时为1的时候,它才是1。也就是当两个开关同时闭合的时候,我们的灯泡才会亮,它才是1。其余只要有1个没有闭合,只要A、B有一个是0,那么输出就是0。所以我们的与运算就是这样的逻辑,只要有0,它的输出就是0。而当它俩同时是1的时候,我们的结果才是1。
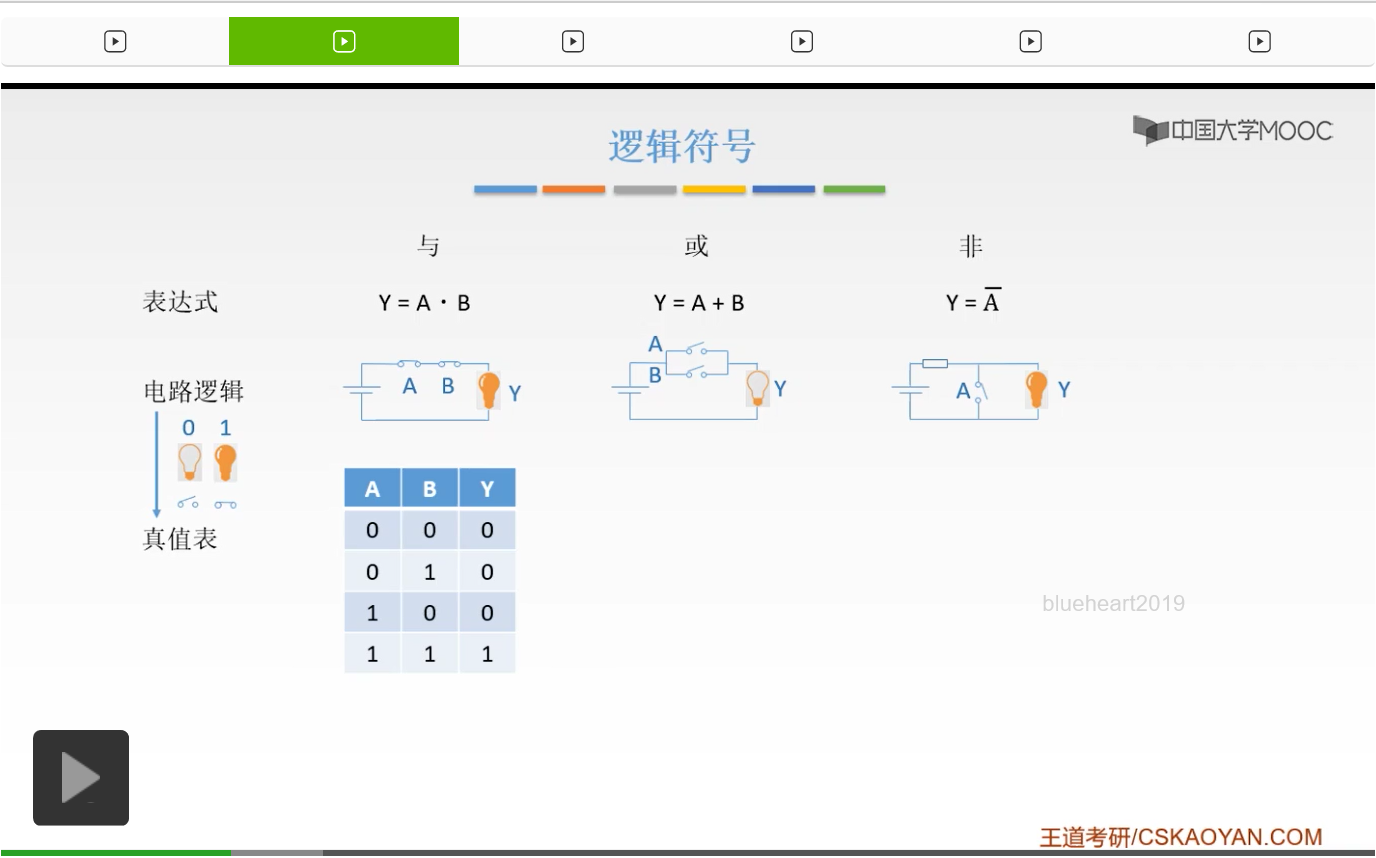
同样的给出我们的或运算的真值表,或运算我们可以把它看成是开关的并联。开关并联就是说,只要A、B有一个闭合,灯泡就会亮,所以只要有A、B,有一个是1,它的结果都是1。只有当A、B同时断开,当A、B同时是0的时候,它才是0。所以我们的与运算和或运算,这个真值表大家应该都非常熟悉了。

而非运算就相当于一个取反,当A是0的时候结果是1。当A是1的时候,结果是0。你可以把它看成是一个短路。那么这就是我们的与或非三种最基本的逻辑运算。

下面给出它的数字电路符号,有两套版本。方框的呢是国标,而右边的那个呢是国际上通用的符号。这要看大家的教材,和出题的这个使用的图形,这两种符号呢大家都要掌握。因为说不定它考试的时候用的是哪一套符号。那么左边的呢就是我们的国标,它是一个方框。如果它里面是一个and,也就是相当于一个与嘛,它的英文,and。那么它就是一个与。而如果是它里面写的是大于小于1,也就是说你只要有1个是1,它就是1。所以呢,当看到大于等于1的时候呢,这就是一个或的符号。而里面如果写了一个1并且外面有一个小圈圈,那就是非的符号。这是国标。第二种呢就是,如果它是一个,左边是一个直直的这样的东西,是一条直线,那么它是一个与符号。如果它的左边是一个弯的,并且它的右边比较尖,那它就是一个或符号。如果它是一个三角形,右边也有一个圈圈,那它就是非的符号。注意,非的符号它都有一个圈圈。这个圈圈呢,就代表一个非。所以大家应该都记住了,这三个符号一定要把它记住。
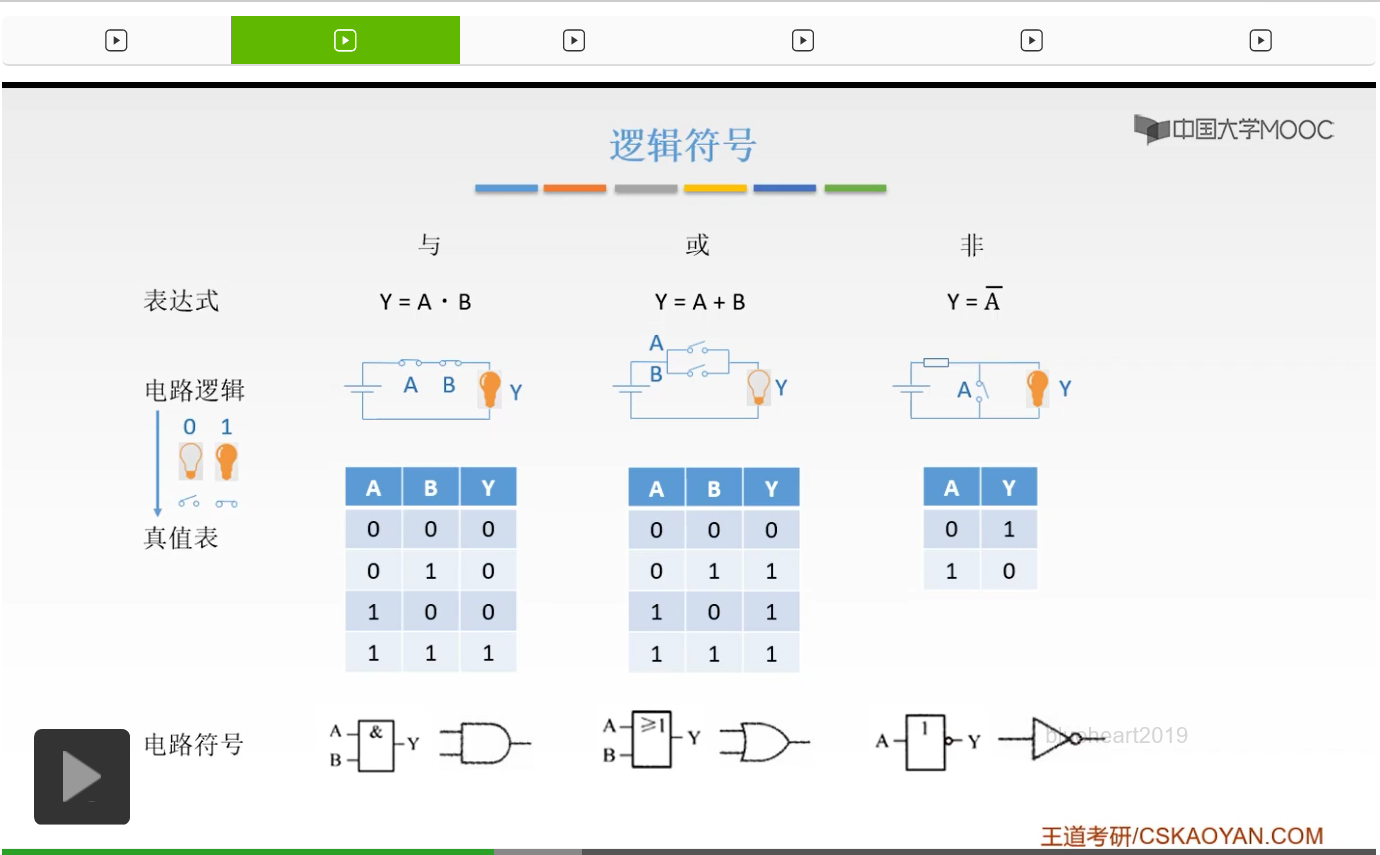
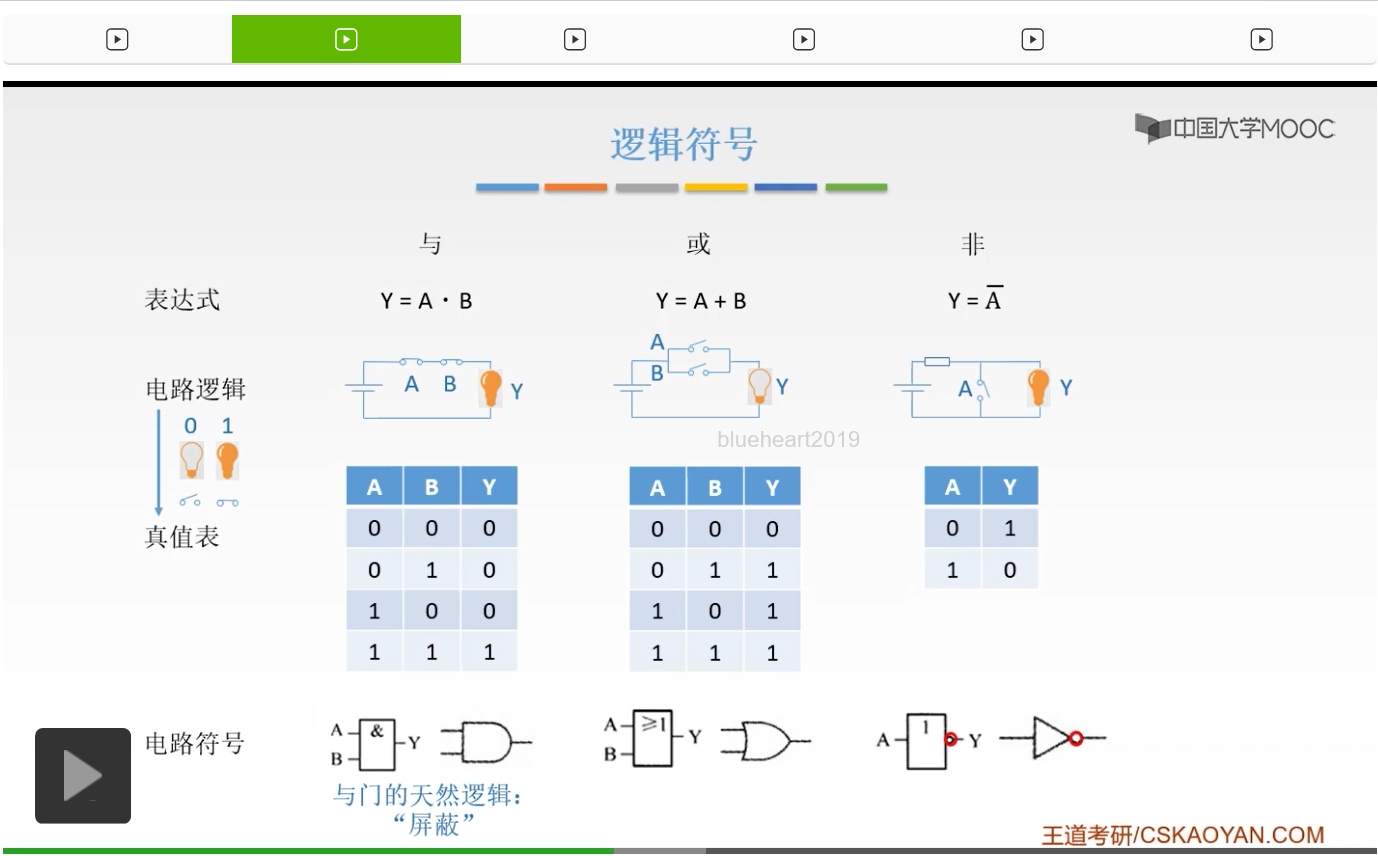
那么与门它有一个天然的屏蔽的作用。为什么呢?我们可以看到这样一个真值表。如果当A是0的时候,当A是0的时候,B你不管输入是0和1它结果都是0。也就相当于如果A现在是0的话,就把B屏蔽掉了,把B的信号完全屏蔽掉了。就不管你B输入什么我都输出的是0。而当A通的时候,当A是1的时候,它才会产生B的数字信号。那这就是与门的一个天然的屏蔽作用,大家了解一下就可以了,重要的呢还是它的电路符号以及它的真值表。

刚才也讲过了,我们的非门,最重要、最核心的部件是它的一个小圈圈,我们在后面讲与非或非的时候关键就是这样一个圈圈。大家要把它的真值表和它的电路符号都记住。
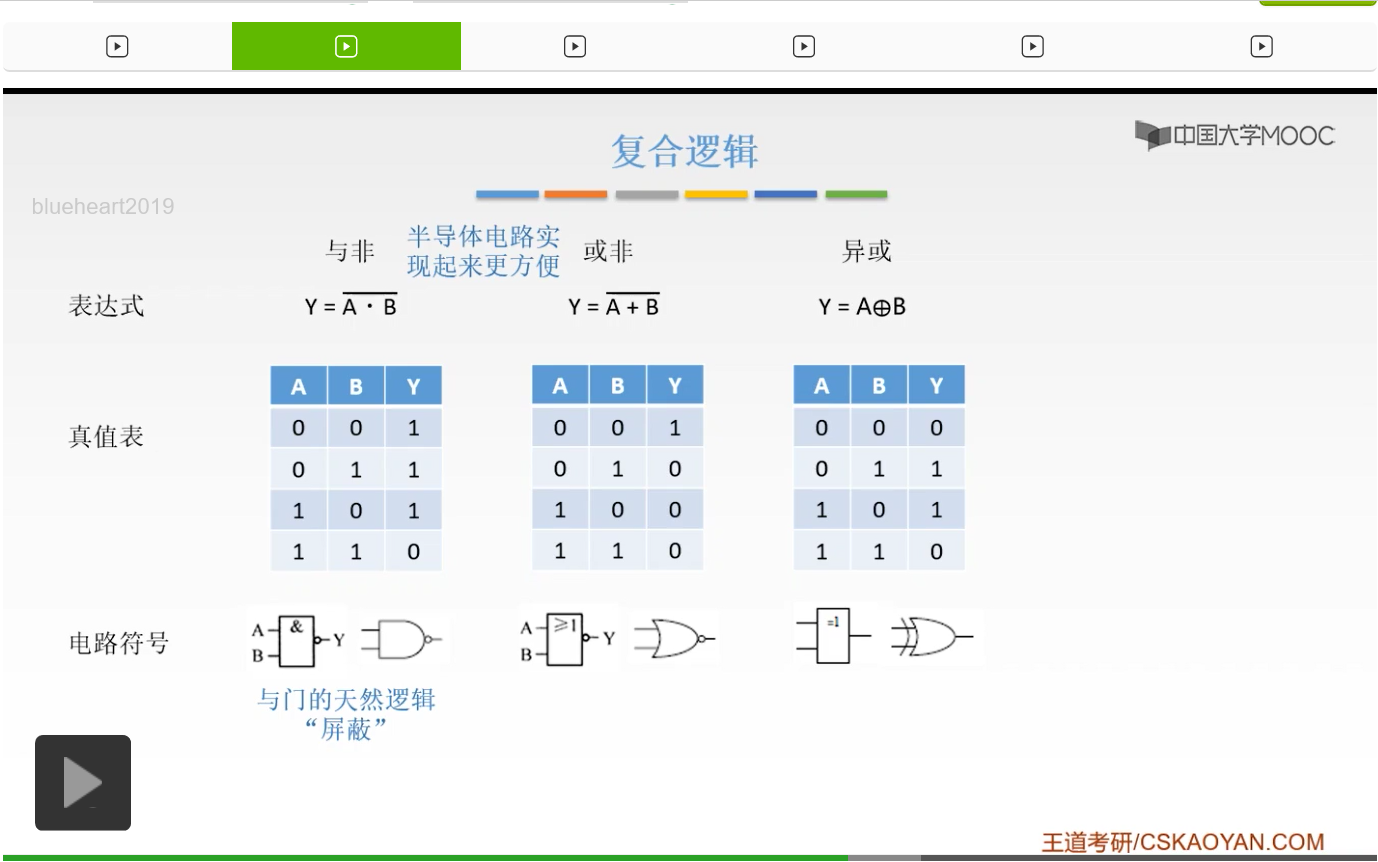
下面要讲的呢是一个复合逻辑。复合逻辑呢就是与非或非和异或,这是最常用的三种复合逻辑。什么叫与非呢?就是在与运算上面再加一个非,也就是与非。它就是把与逻辑上面加一个非,也就是把与逻辑的真值表全部取反,所以当A和B同时是1的时候它输出0,其他情况都输出1。这是和与门相反的。那么它的电路符号就是在与门的基础上加一个小圈圈,刚才也讲过了,圈圈代表的就是非。所以这以后看到这样的符号就是与非。那么或非同样的就是在或门的基础上加一个非门,也就是在或运算的基础上加一个非运算,所以它的真值表和非运算是相反的。当A和B同时为0的时候它才输出1,其余情况都输出0。那么有了与门和或门为什么还要有与非和或非呢?原因是这样。

半导体的电路实现起来是比较方便的,也就是我们的电子技术在实现这样真正的电路的时候,半导体电路实现与非和或非比实现与门和非门要容易的多,所以与非和或非我们更常用。

那么与非门和与门同样的都有一个天然的屏蔽的一个作用,也就是说当A是0的时候,不管你B输入什么我输出都是1。而且我当A是1的时候,我才会把B的输入信号返回出去。与非门和与门的同样的这样一个屏蔽的作用。
那么再给大家讲一下
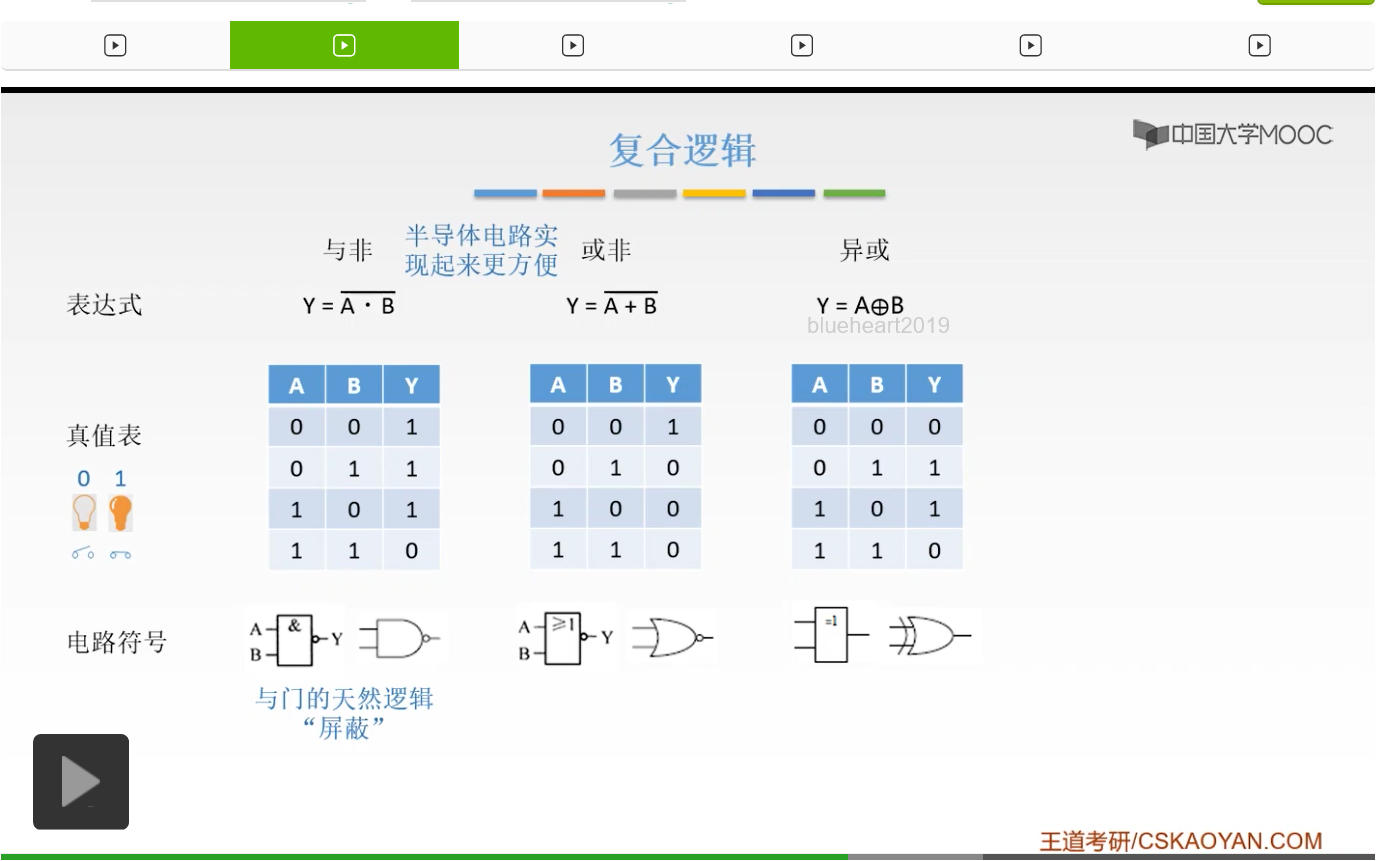
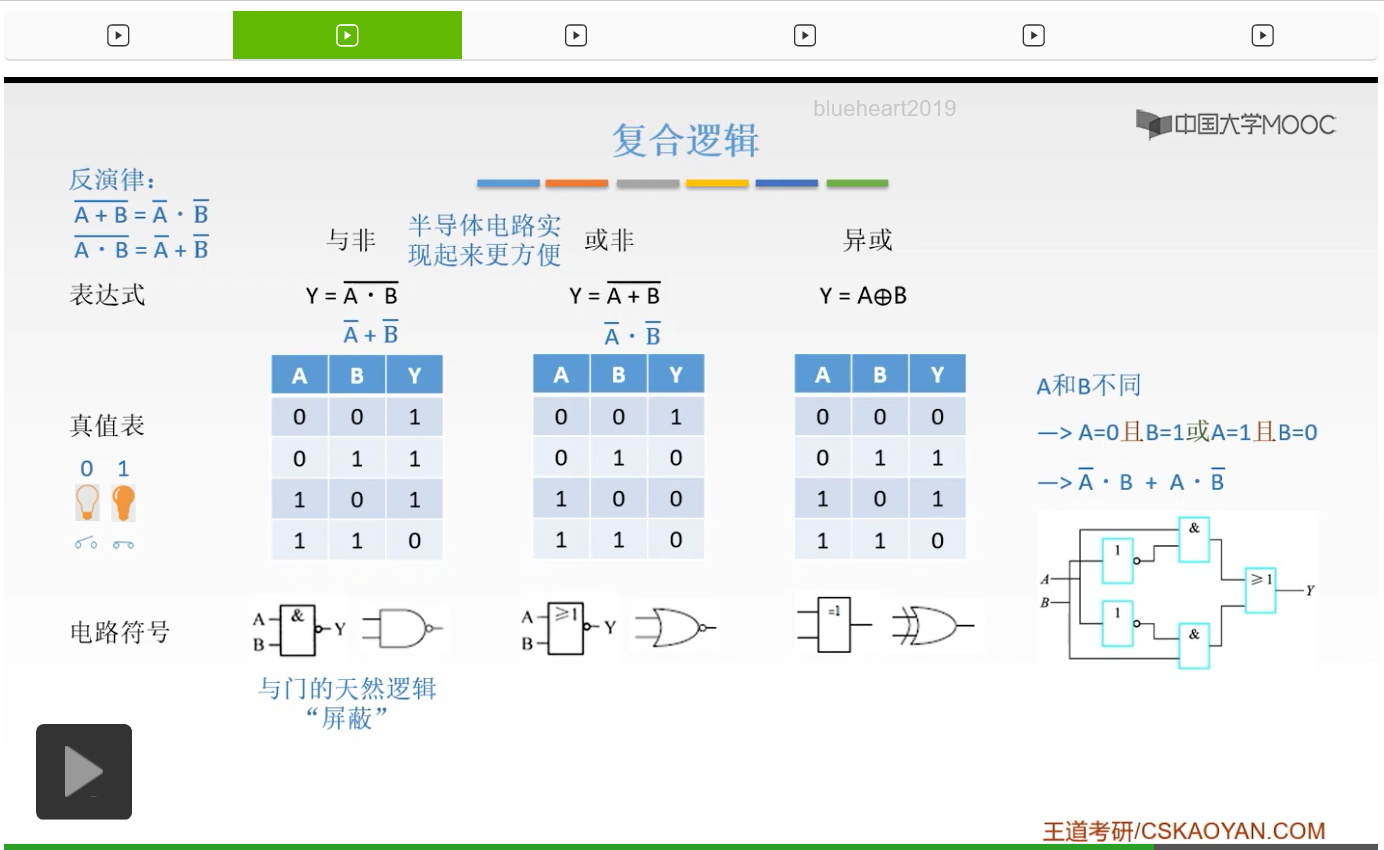
反演率,这个大家做一下了解就可以了,因为我们这一门课重要的还不是数字电路,这在数字电路当中是非常重要的,但是我们只是讲解它的应用,所以反演率呢大家看一下就知道了。那么反演率的具体内容是什么呢?也就是说或非门相当于A非与上B非。同样的与非门相当于是A非或上B非。啊大家这个大家了解一下就可以了,不需要做太多的深入的掌握,因为我们毕竟这一门课是计算机组成原理而不是数字电路基础,所以只是简单讲一下就行了。

那么异或我们之前已经碰到过好多次了,大家对它已经非常熟悉了。异或呢就是说当A和B不一样的时候,它输出是1,其余情况也就是说当A和B同样的时候,它输出的是0。我们是判断A和B不同的时候。

所以我们之前在讲校验码的时候就已经用到过它了,也就是说当A是0B是1的时候,或者A是1B是0的时候,只要它俩不同,输出的结果就是1。其他情况也就是说当A和B相同的时候输出是0。

我们可以把它改写一下,也就是说异或是怎么来定义的。异或定义的就是说,A非与上B或上A与上B非,这就是它的定义式。只有当A和B不一样的时候结果才是1。我们可以把它代进去验证一下,当A是0B是1的时候,A非是1B是0,所以AA非与B是1。同样的,A与B非它是0,所以或起来它就是1。所以异或就是这么定义的。

那么异或呢我们就可以用非门和与门还有或门把它实现,也就是说用两个非门,然后把A非与上B,然后再或上A与上B非,那么这就是异或的一个逻辑。同样的呢如果我们看到了这样一个符号,框框里面是等于1,那么这就是一个异或门。或者呢在我们的或门基础上,前面加了一个小弯弯的这样的东西,那么这就是一个异或门,大家要熟悉。
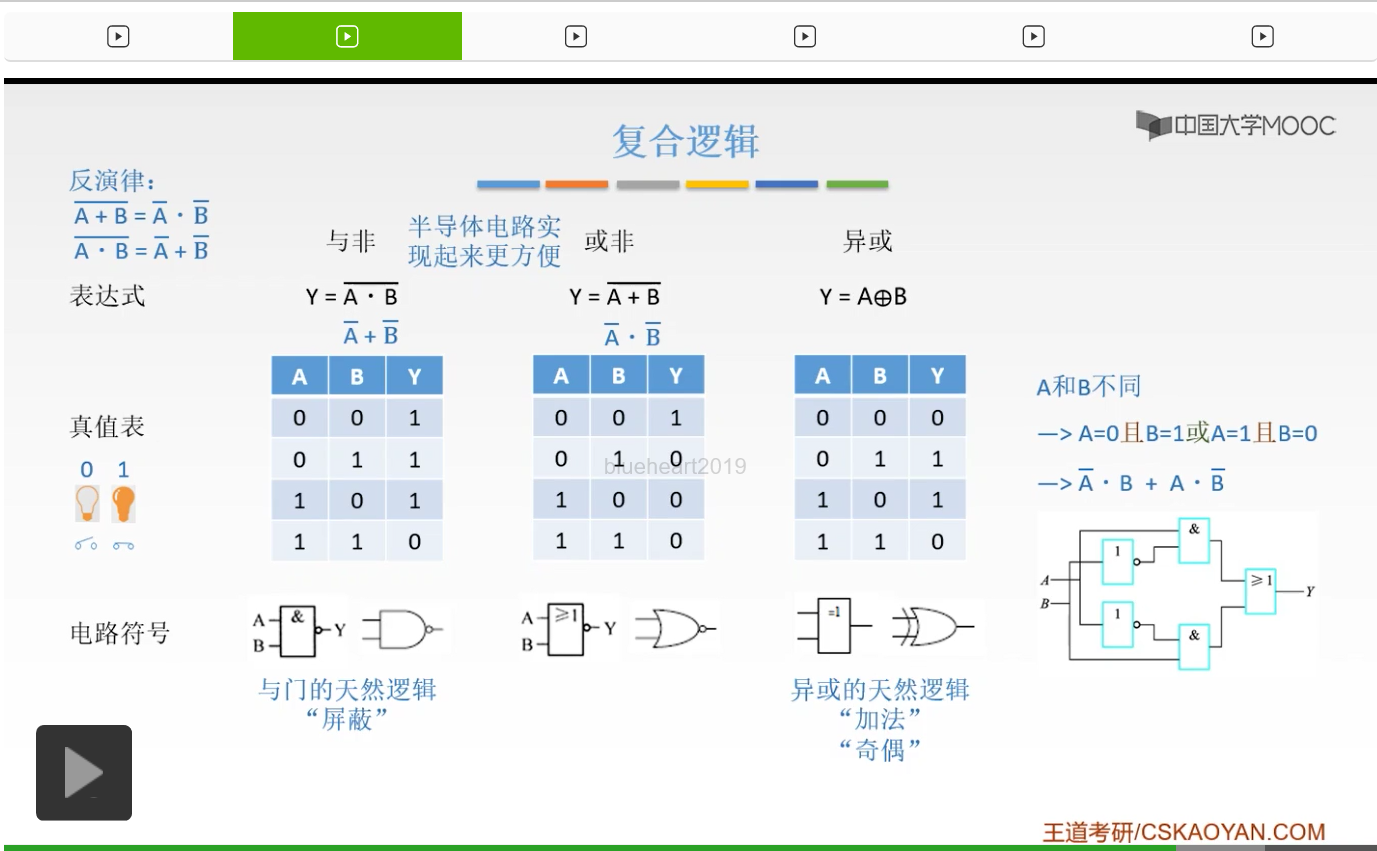
那么我们之前也讲过了,异或门,它呢可以用来进行一个奇偶校验。同样的呢,我们可以用异或门来实现加法操作,也就是我们的加法器就是在异或门的基础上实现出来的。为什么这样说呢?
我们来看一下这样的一个例子。我们知道二进制加法呀,它是0加0等于0,0+1等于1,1+0等于1,1+1等于10。我们先看它的这个最末尾,我们可以看到它和异或门的真值表是一一对应的,完全相同的。所以我们的最低位完全就可以用我们的异或门来实现。

如果我们把最高位补上,也就是说把它的这样的0全部补上的话,
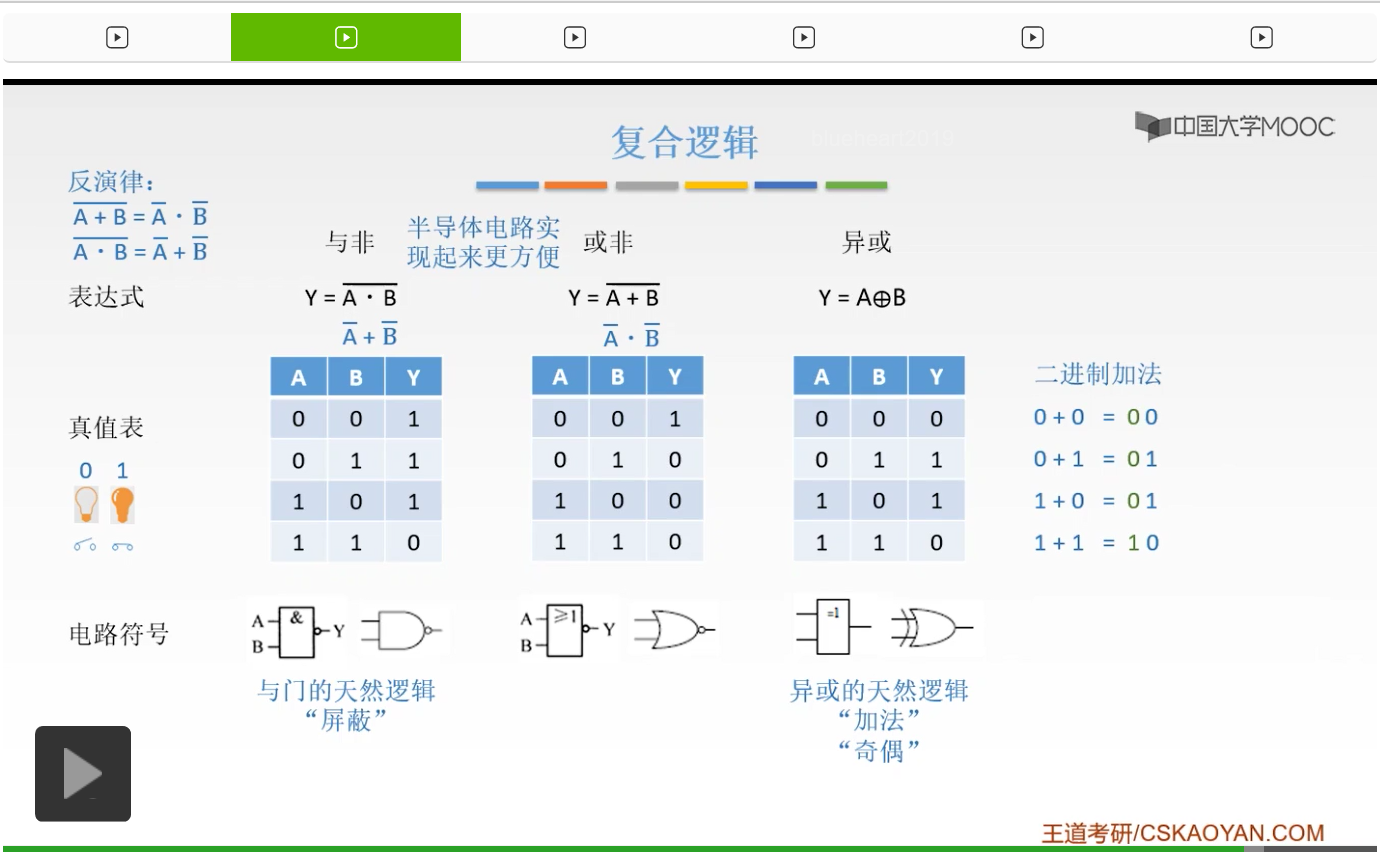
我们可以看到和与门的真值表是一致的。也就是说我们的最低位和异或门的真值表是一一对应的。

而我们的高位和与门是一一对应的,所以我们就完全可以用与门和异或门来实现我们的加法操作了,这是后话了。我们现在只是告诉你异或它有一个天然的加法的逻辑,那么这是我们最常用的三个复合逻辑。
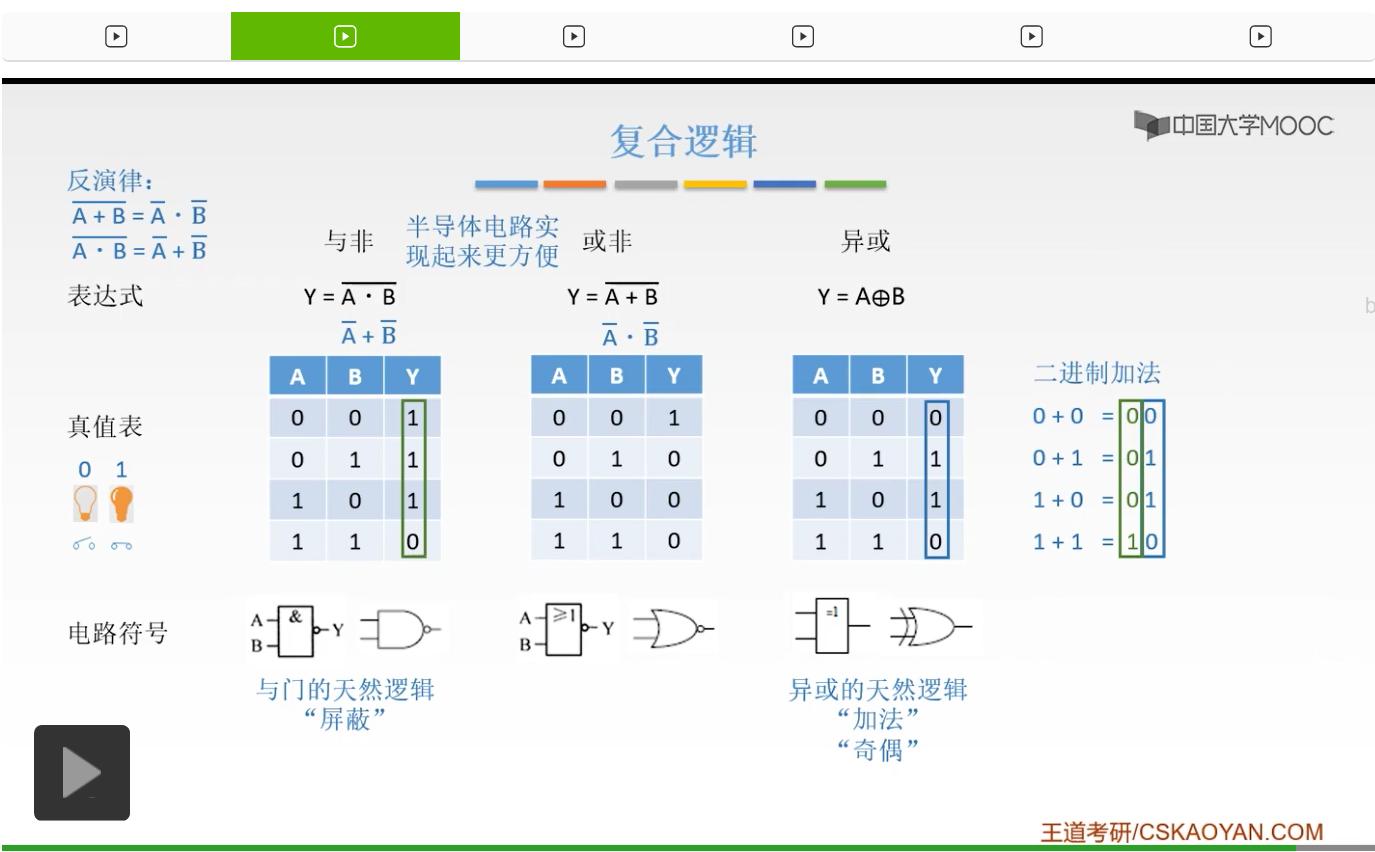
最后,再介绍一个不太常用的叫做同或的逻辑。同或呢就是在异或基础上取个非,你理解一下就是取个非就行了,所以呢同或不太常用。如果可以用同或实现的,我们完全可以用异或来实现。所以同或大家只要了解一下就可以了,那么本节的内容就告一段落。我给大家补充了数字电路的一些知识,相信大家已经对数电有一个基础的了解了。掌握这一些最基本的东西就完全可以应付我们的计算机组成原理要用到的一些数电的知识了。
那么本节我们将要讲解加法器的实现原理。

首先讲解的呢是一位全加器。有了一位全加器的基础之后,我们就可以实现我们的串行加法器和并行加法器了。

那么我们之前在讲数字电路的基础知识的时候就已经提到过,我们的异或,和我们的与,完全可以实现一个一位的二进制式的加法。那么我们的最低位就可以用我们的异或来实现,最高位用我们的与来实现。

那么我们把两个拼接到一起,就可以实现我们的一位二进制数的加法了。也就是0+0得到的呢是0,0+1得到的是1,1+0得到的是1,1+1得到的是10。
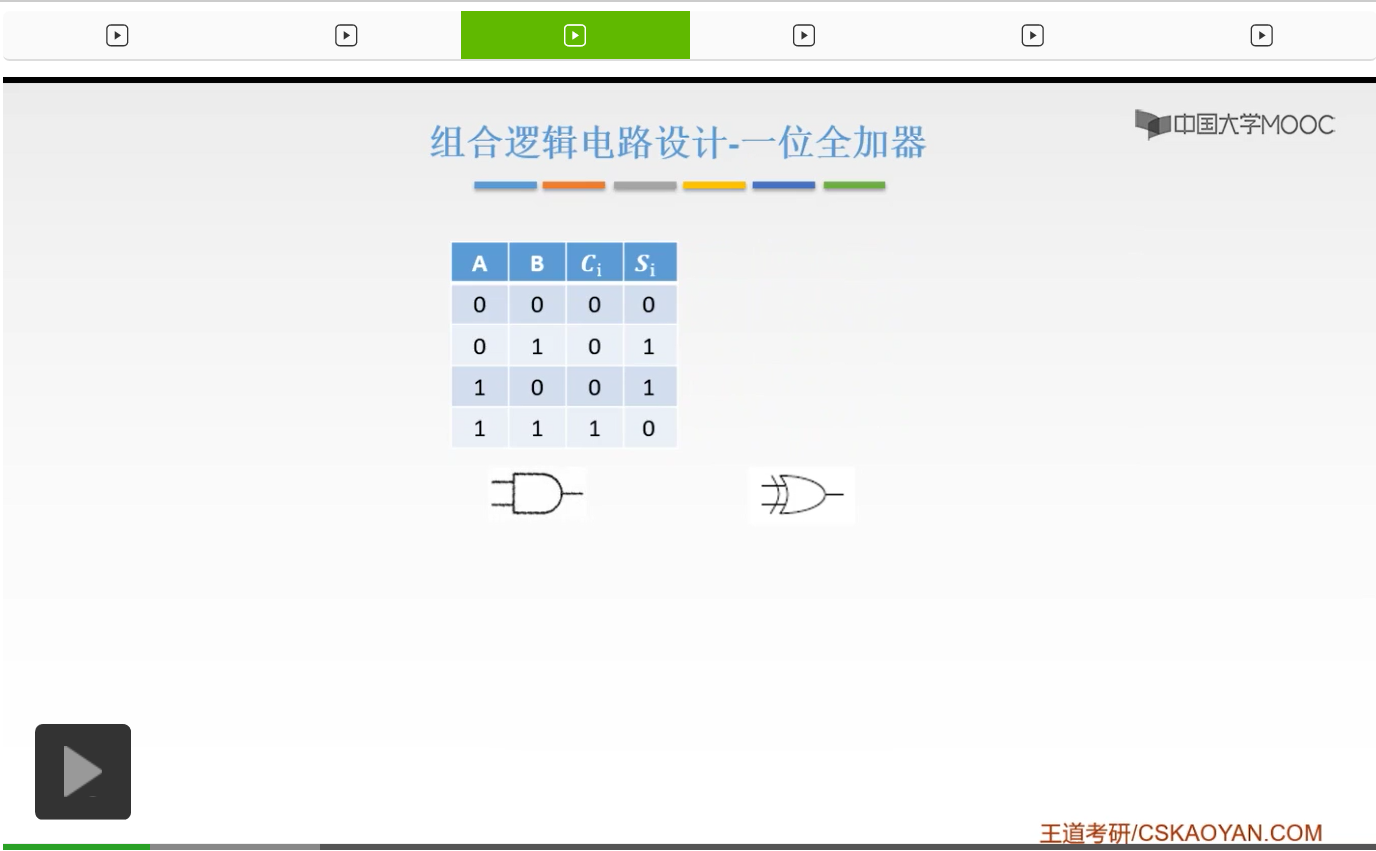
那么我们就可以用这样的一个电路来实现它。我们的这个线上传递的都是输入信号。比如说我们的A可以通过第一条输入信号和我们的B经过第二条输入信号得到的呢就是我们的A与B,也就是Ci。然后我们的A再经过下面的,和B经过下面的,然后经过一个异或门得到的呢就是A异或B,就是我们的最低位Si。光是这样是不够的,为什么呢?

因为我们的加法是怎么来实现的呢?不带有我们本身的这两位数,还要接收我们低位给我们的一个进位信号,这样才能完成一个完整的加法。如果光是我们现在实现的这个东西,是远远不够的。这只能进行一个两个一位的二进制数的加法,但并不能由此得到我们好多位的一个加法,这是不够的。缺少了什么呢,缺少了我们低位的一个进位信号。所以呢我们现在实现的这个东西呢叫做半加器,而我们现在要实现的呢叫做一位全加器。
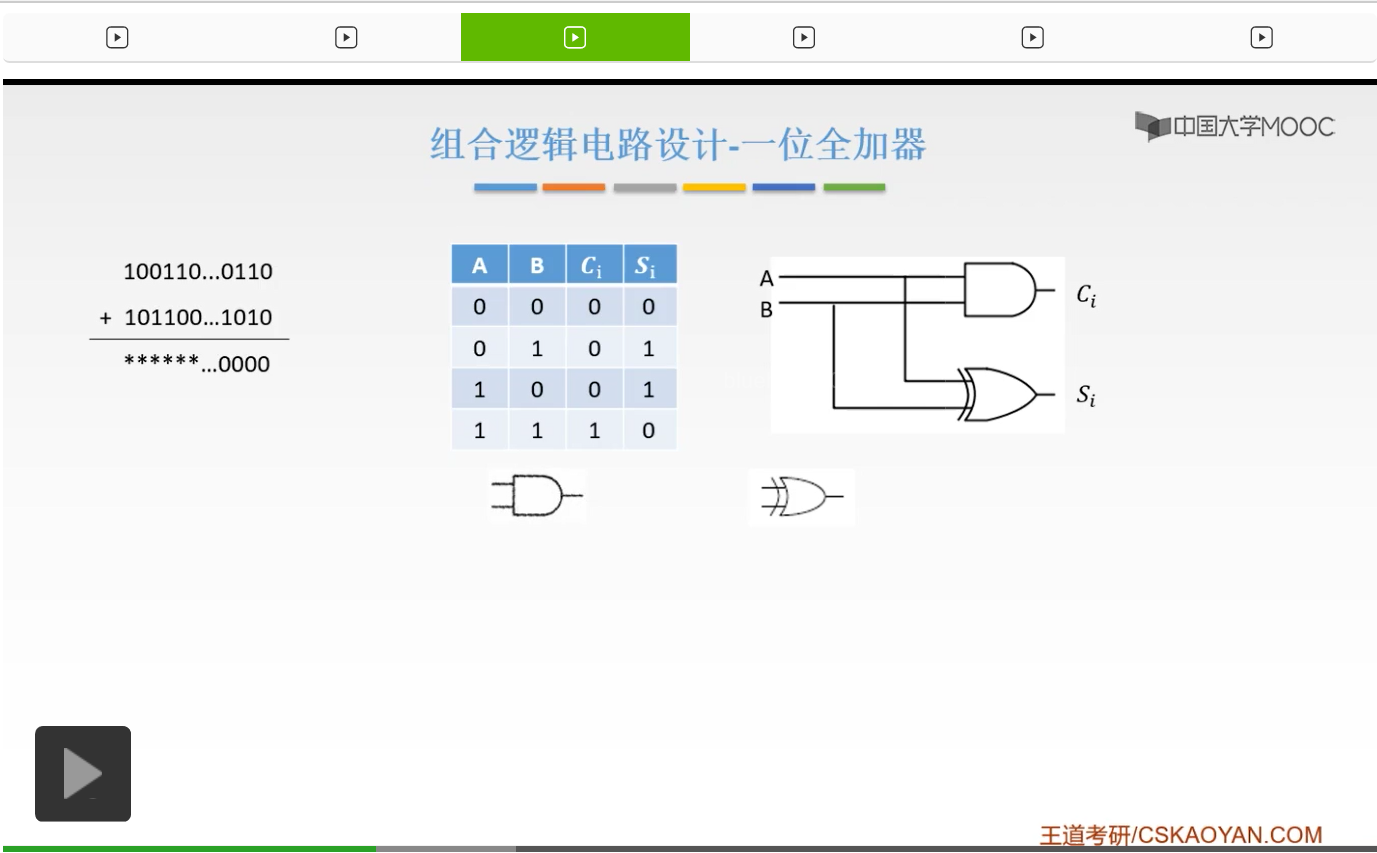
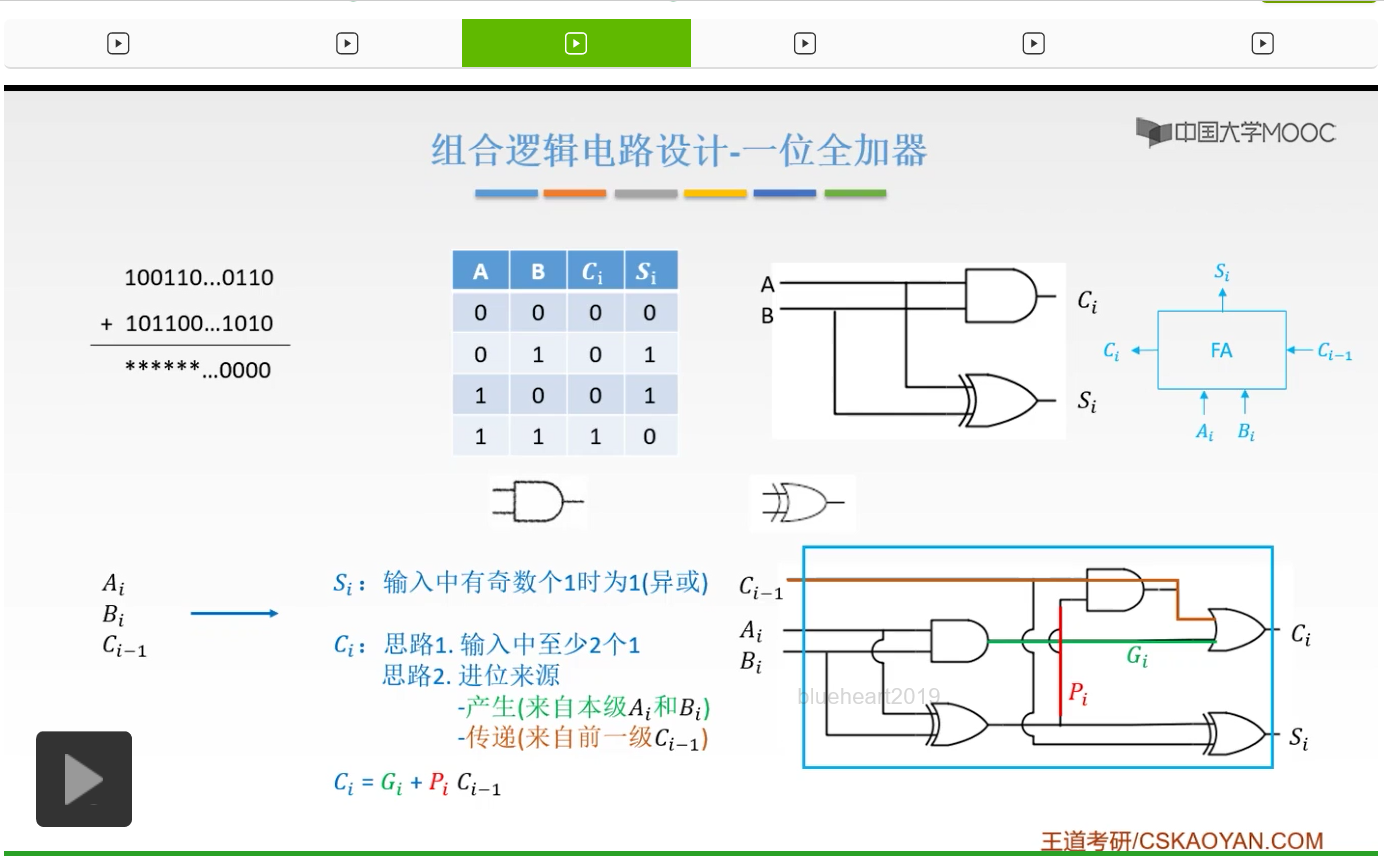
也就是不但要有我们的Ai,Bi,还要一个低位的进位信号也就是Ci-1,由此得到一个Ci也就是进位,然后Si是我们的结果。
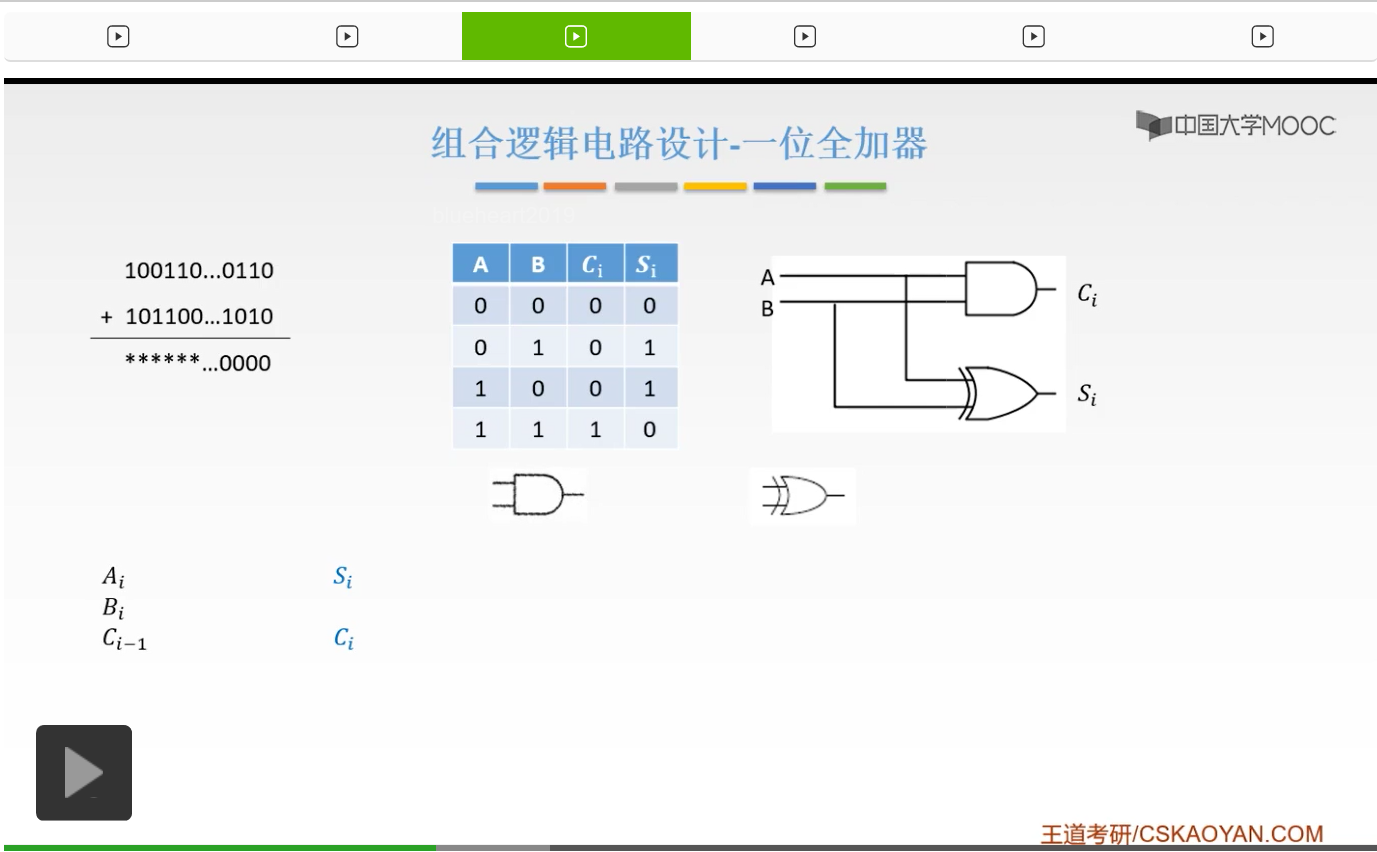
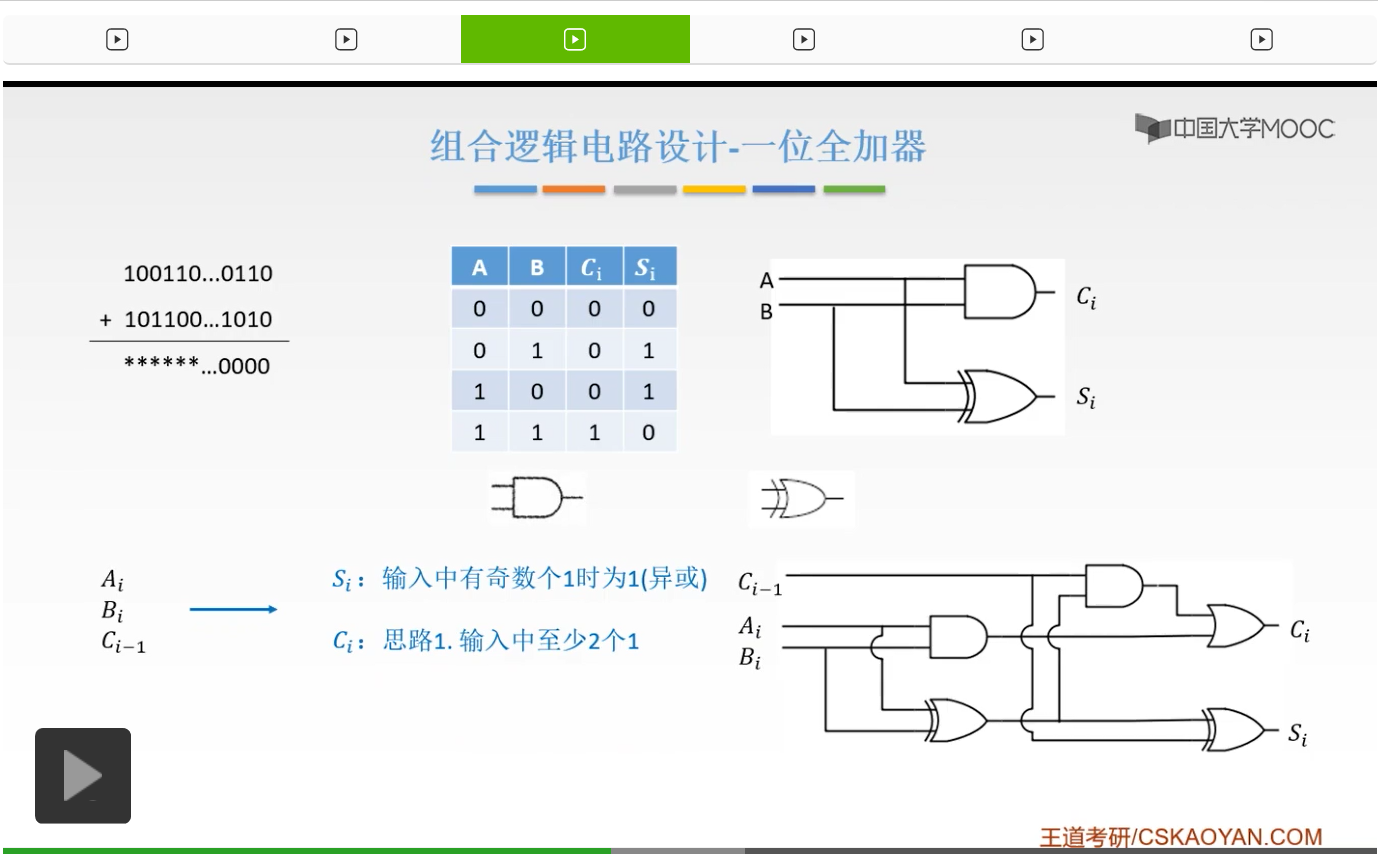
所以呢通过这一个,我们就可以实现一个一位的全加器。那么它是怎么得到的呢?Si是怎来的?
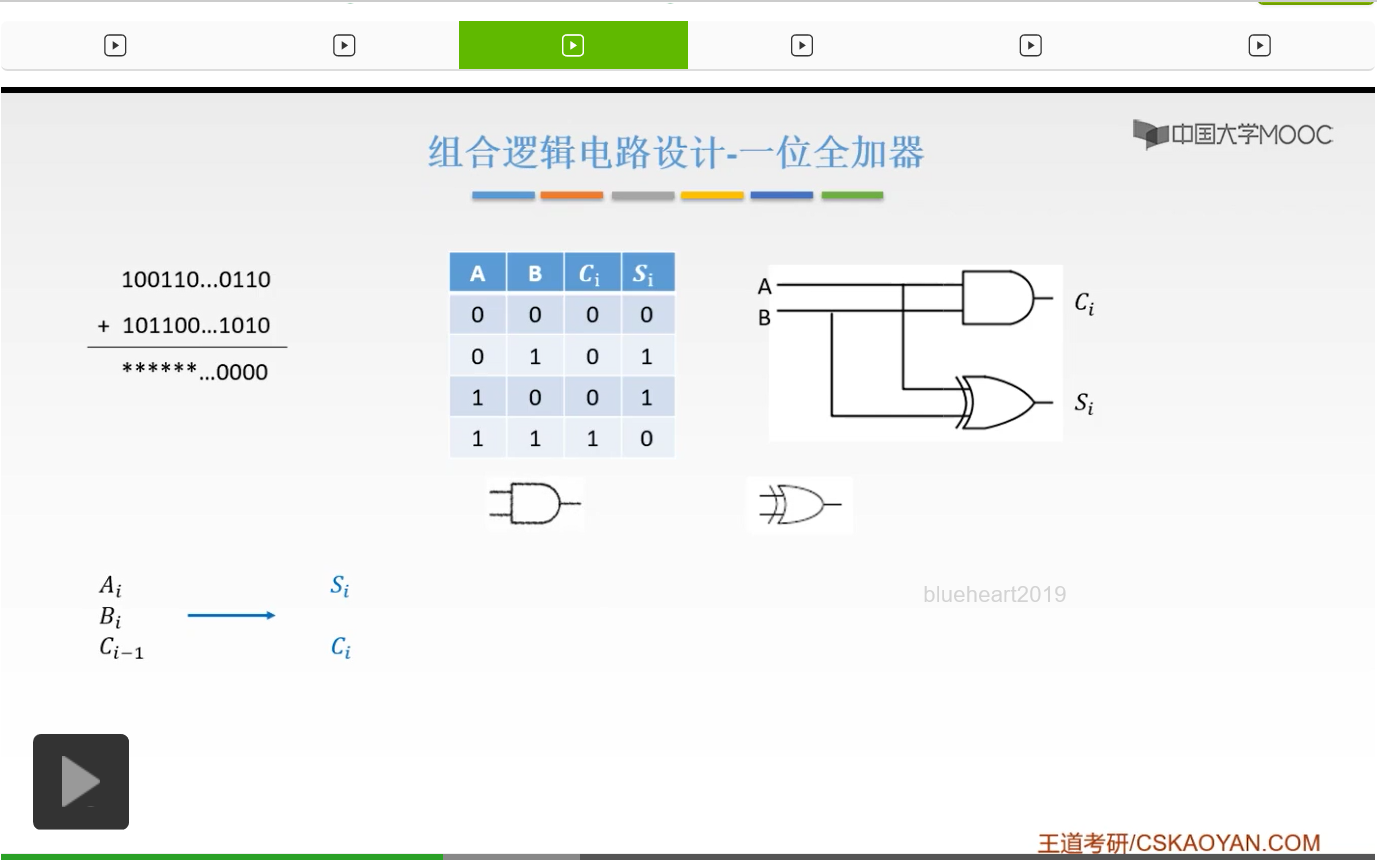
Si就是说只要输入当中有奇数个1的时候,我们就可以是1。比如说001,0+0+1它是1,而0+1+1呢,它是10对吧,所以Si应该是0。而1+1+1,它才是11,所以它Si才是1。所以输入有奇数个1的时候,Si才为1。所以我们就可以用异或门来实现。
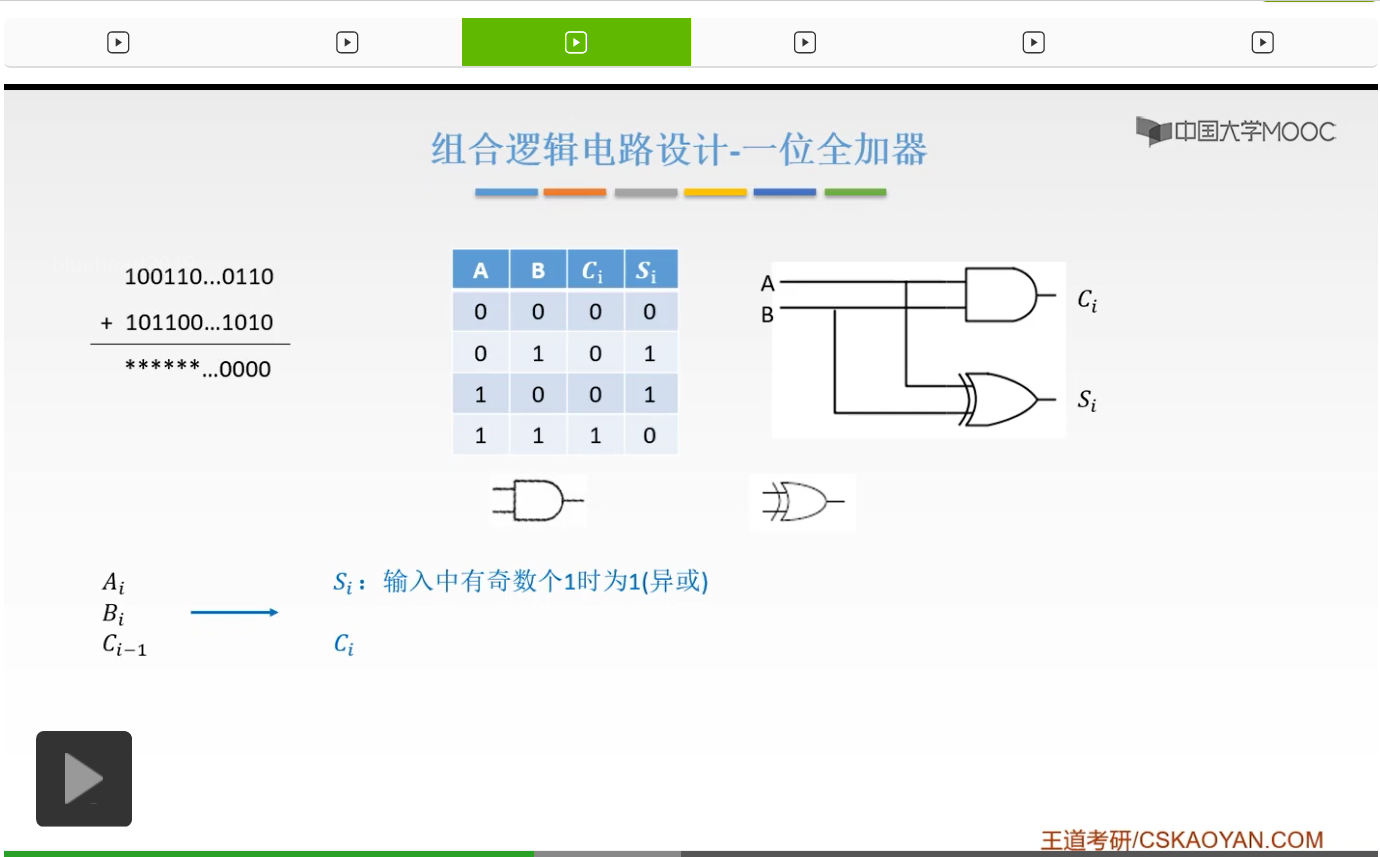
而Ci也就是我们的进位信号是怎么得到的呢?第一种思路就是说我们的输入当中至少有两个1的时候,你有两个1你才能产生一个进位对吧,才能产生一个10。而三个1的时候呢,11对吧,至少有两个1,它才能产生一个进位。
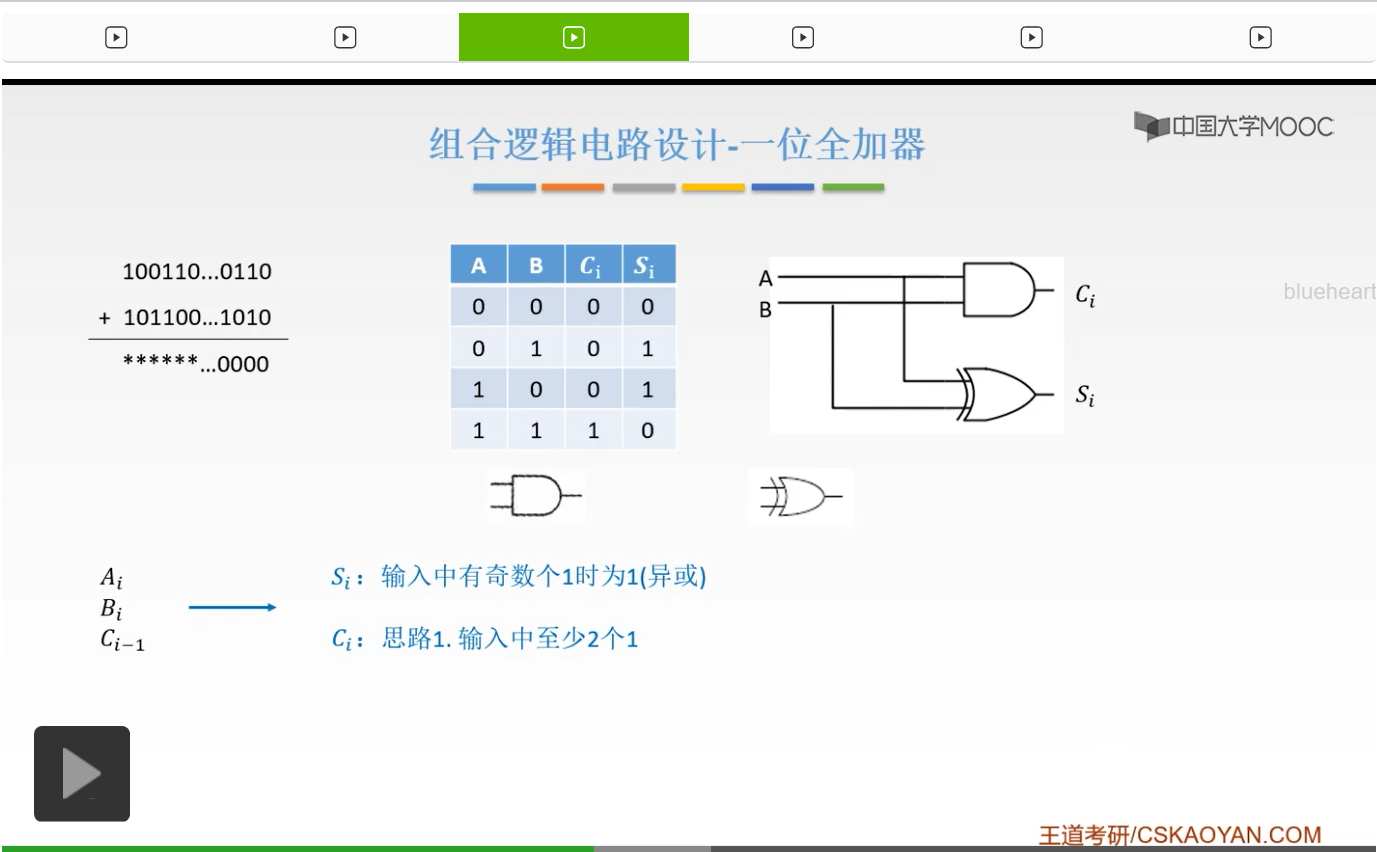
那么通过这两个我们就可以得到一个这样的全加器。
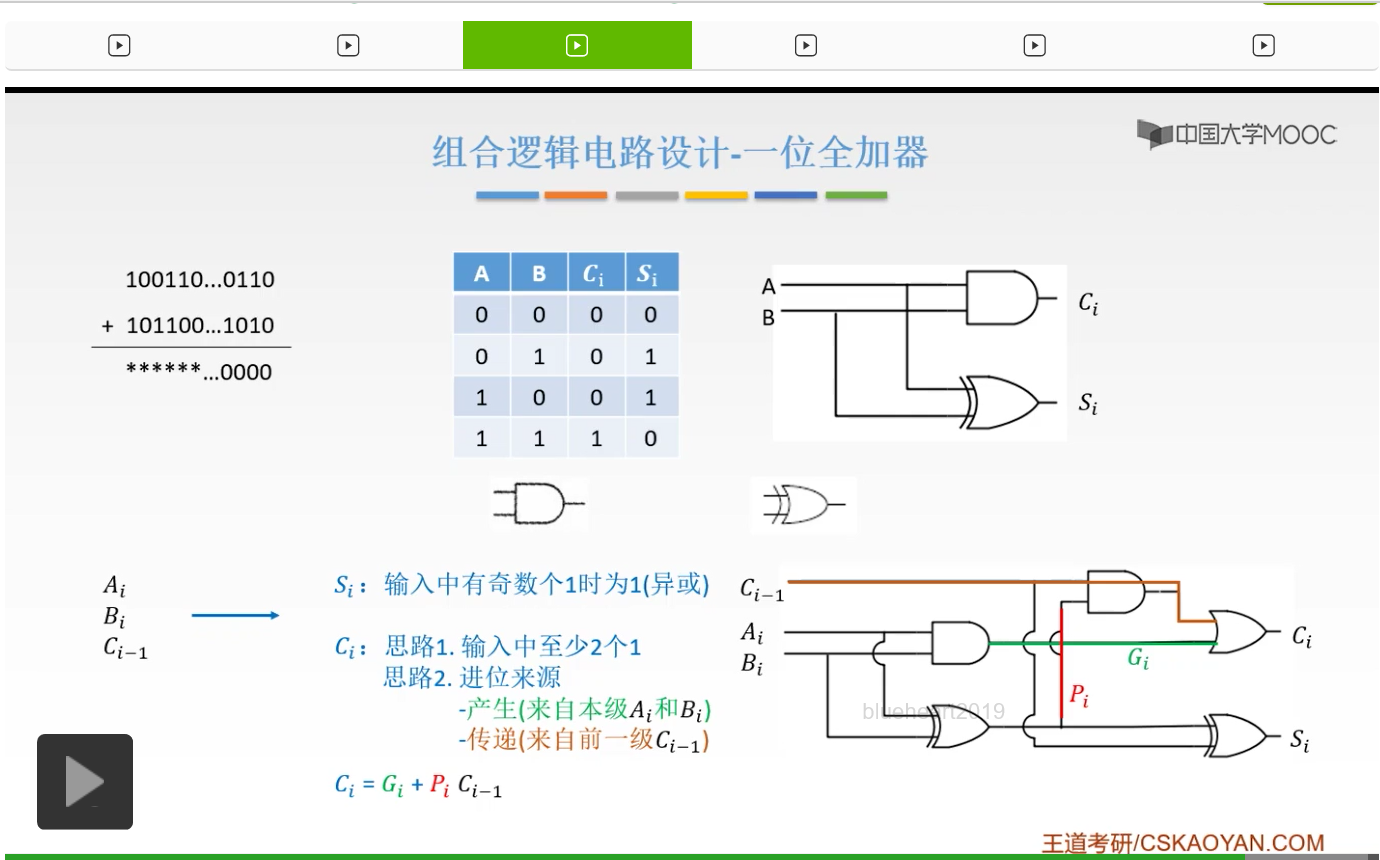
但是这样呢理解起来是比较麻烦的,所以呢我们就来分析一下我们的进位是如何来的,我们是怎么得到我们的进位的。第一种是由我们Ai和Bi,本身产生的一个进位。只有当Ai和Bi,两个都是1的时候,也就是1+1我们才可以得到10。

这是由我们本级的Ai和Bi得到的一个进位,我们把它叫做产生,也就是我们绿色的这根线。所以呢当Ai和Bi我们用一个与门把它连接起来,只有当A和B同时是1的时候,它才会产生一个进位信号,是用绿色的线呢连接起来的,这是一个产生的进位信号。还有一种呢就是传递的进位信号,也就是说我们的这个进位是怎么来的呢?通过我们前一位给我们的进位信号,我们现在才有一个进位信号,那么这个呢叫做传递的进位信号。

它是怎么来的呢?首先有它一个自己,我们用橙色的线来标注出来,就是它自己。还有呢,还有就是说我们的A和B,它俩有一个是1,因为它俩都是1的情况我们已经分析过了这是一个产生的进位信号。当它们俩个有一个是1的时候,它才会有一个进位。如果两个都是0的话是不可以的,如果两个都是0,0+0再加1个1,它是不会产生任何进位的。所以只有当Ai和Bi有一个是1的时候,我们才会和Ci-1结合起来产生一个进位信号。所以是10和01,也就是说不同。

所以呢我们可以用一个异或门来实现,也就是说Ai和Bi进行一个异或之后,再和Ci一起产生一个进位信号。这是一个传递的进位信号。所以我们进位有两个来源,一个是Ai和Bi两个自己产生的一个进位信号,也就是说Ai=1,Bi=1,它是一个自己产生的进位信号。第二种情况呢是Ci-1带过来的一个进位信号。所以当Ai和Bi有一个是1的时候,并且Ci-1是1的时候,我们才会产生一个进位信号。

由此,我们就可以得出我们的进位信号是怎么来的呢?Ci等于Gi+PiCi-1。Gi是什么?Gi就是我们绿色的这根线,也就是我们产生的同级的一个进位信号。而Pi呢,Pi就是A和B它俩,一个是0一个是1,进行一个异或之后产生的一个逻辑。然后Pi再乘以一个Ci-1,就是Pi和与上Ci-1,得到的是我们的传递的进位信号。然后它们两个之间用一个或门进行连接。也就是说,只要有一个产生了进位,那么都会有一个进位。所以Ci,就是这么来的。大家再回顾一下。Ci是怎么来的呢?有一部分呢是Ai和Bi,它俩都是1,就不考虑Ci-1的时候,它们俩个都是1的时候,才会有一个进位。如果考虑到我低位给我的进位信号之后,只有Ai和Bi有1个是1,有1个是0它才会产生一个进位信号。
它俩如果都是0的话是不会产生进位信号的。
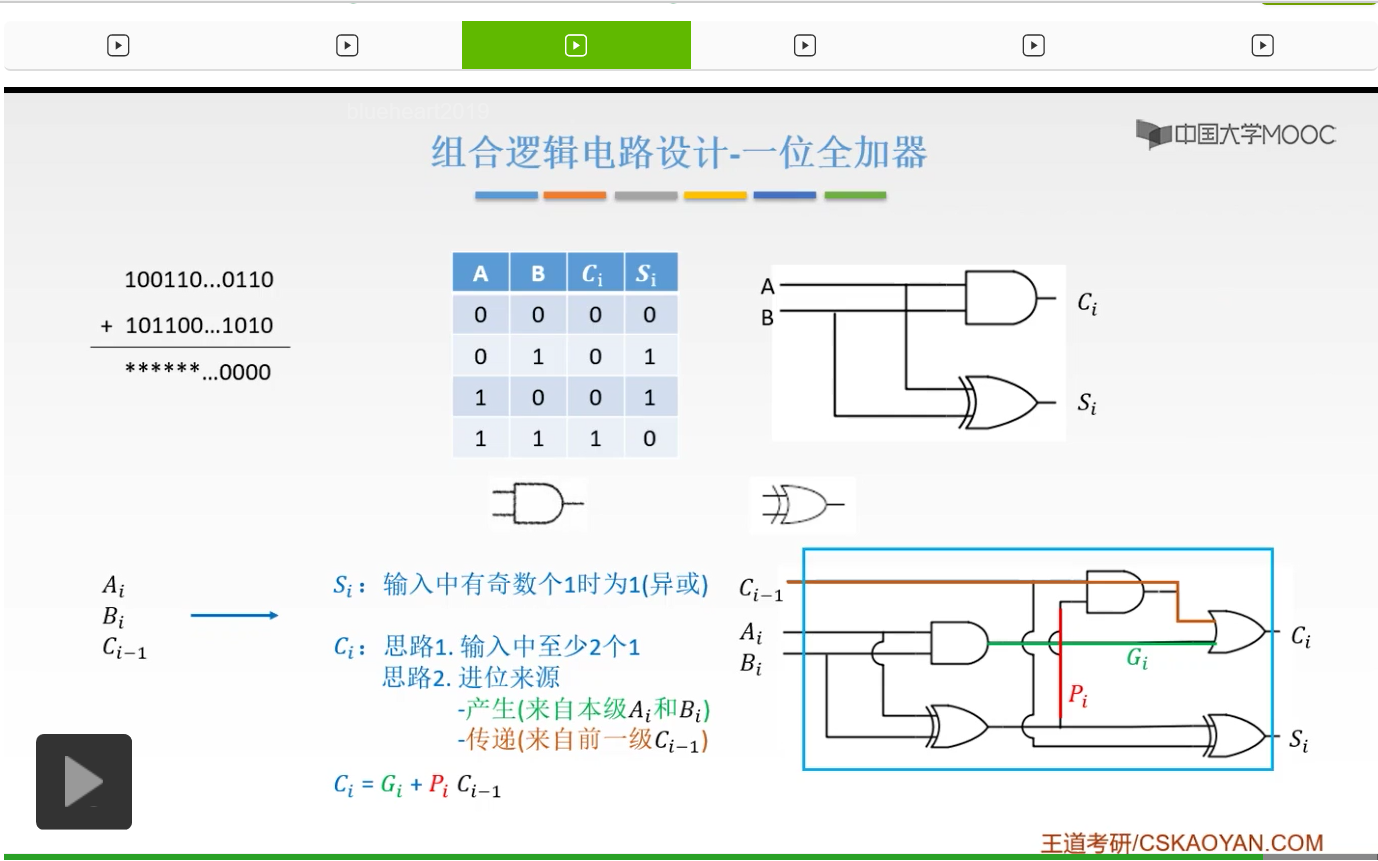
所以这就是我们的一位全加器。是如何构成的大家应该都了解了。
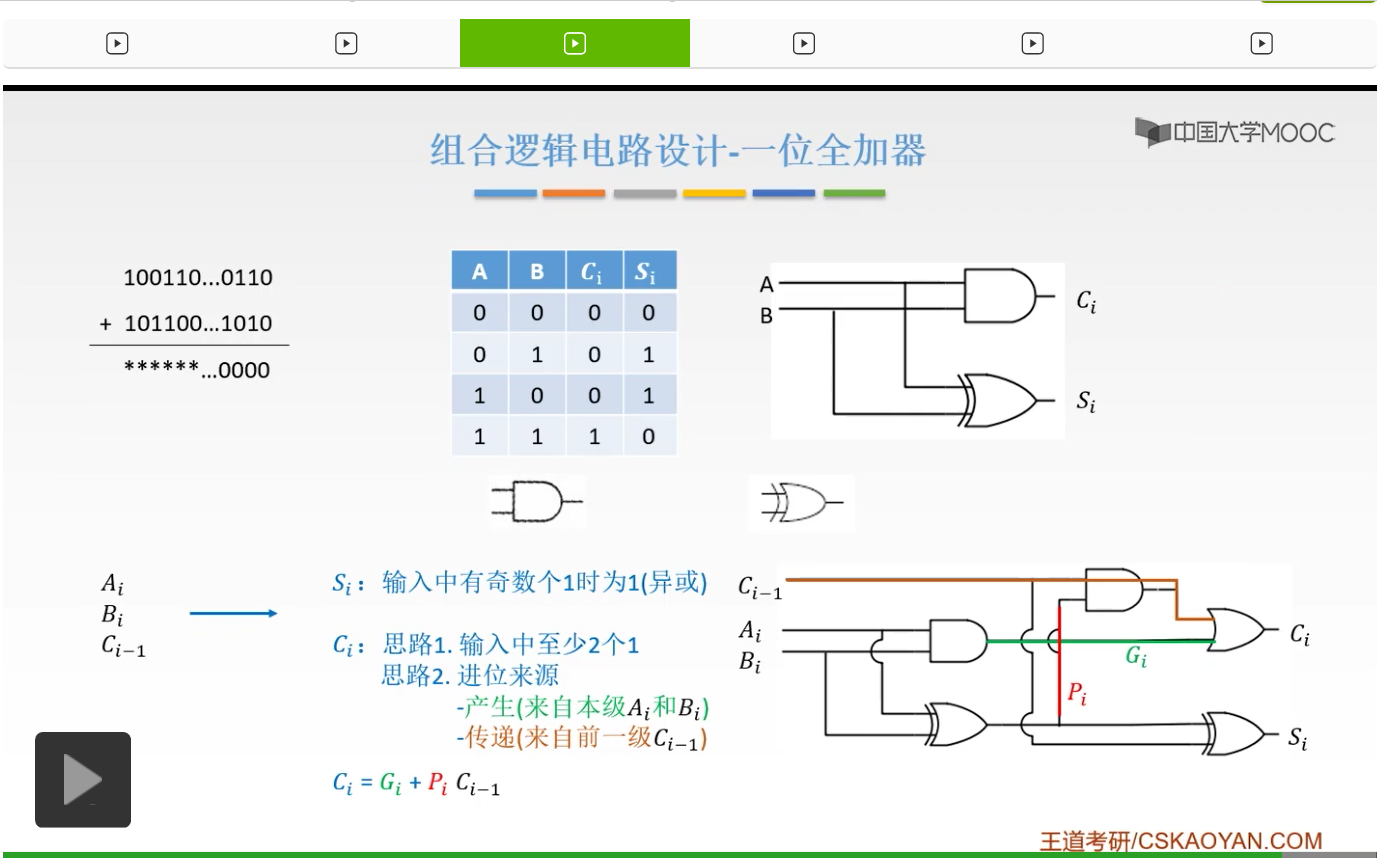
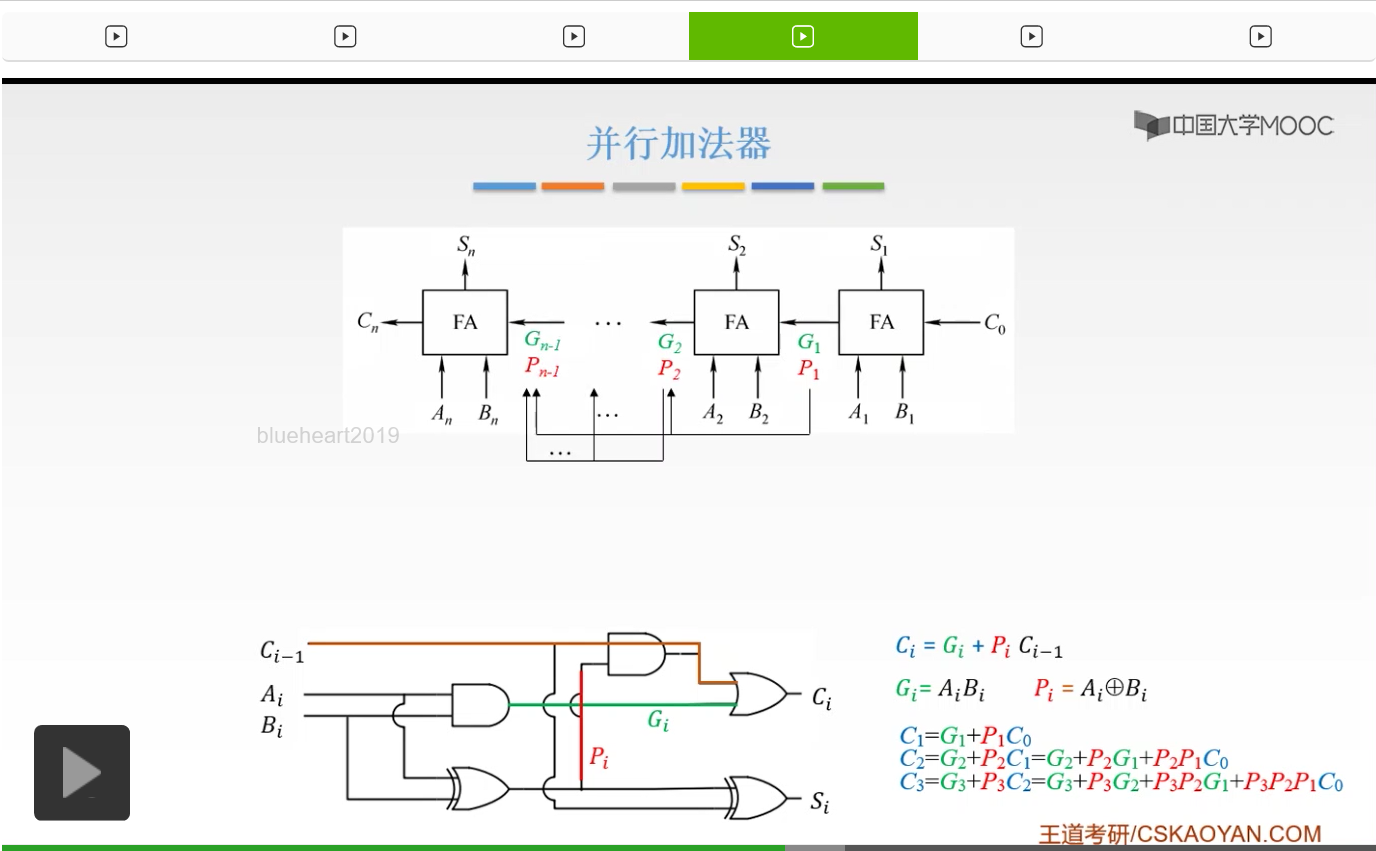
那么把一位全加器封装起来就得到了我们的FA,也就是一位全加器。它接收三个信号,也就是Ai和Bi,还有一个我们低位给我们的Ci-1的一个低位的进位信号,然后产生两个输出信号,一个是Si是我们的结果,一个是Ci,是一个进位信号,所以这就是一位全加器。由一位全加器我们可以得到串行加法器和并行加法器。
有了之前一位全加器的知识,我们就要用我们的一位全加器来构成我们的加法器。
那么有两种形式,第一种形式呢叫做串行的加法器。什么叫串行的加法器呢?在串行加法器当中我们只有一个全加器,只有一个全加器。然后我们的数据逐位地串行地输入到我们的加法器当中进行计算。所以如果我们的操作数乘n位的话,加法就要进行n次,每次呢产生一位的和,然后再串行地逐位送回到寄存器当中。

那么我们的这个进位就送到我们的进位触发器当中。进位触发器呢是用来寄存我们的进位信号的,然后再参与到我们的下一次运算当中。所以我们只有一个全加器。一个全加器来一个一个地一位一位地进行运算,每次呢只产生一位的和,然后我们的进位再进入到下一次运算当中。

那么这就是我们的串行加法器的工作原理,只有一个全加器,然后逐位串行送入到加法器当中进行一个运算,然后用我们的进位触发器来寄存我们的进位信号。
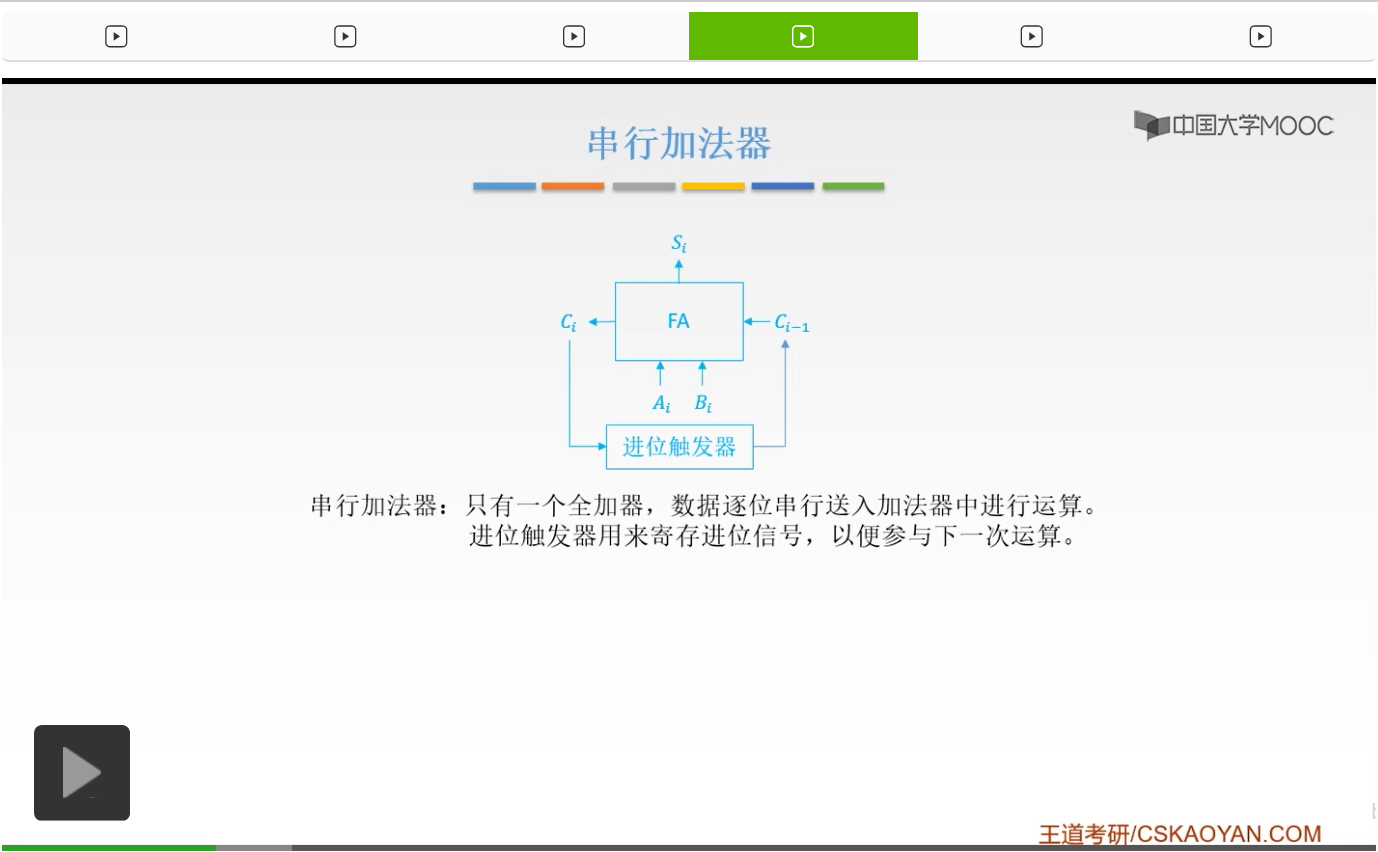
这个刚才也讲过了,我们的操作数如果是n位的话,我们就要进行n次加法。它有什么特点呢?它只有一个全加器,所以它计件少,成本比较低。但是,它的运算是非常慢的,因为是一位一位地进行,很慢,所以这显然是不够的。所以我们可以用多个全加器来构成加法器。

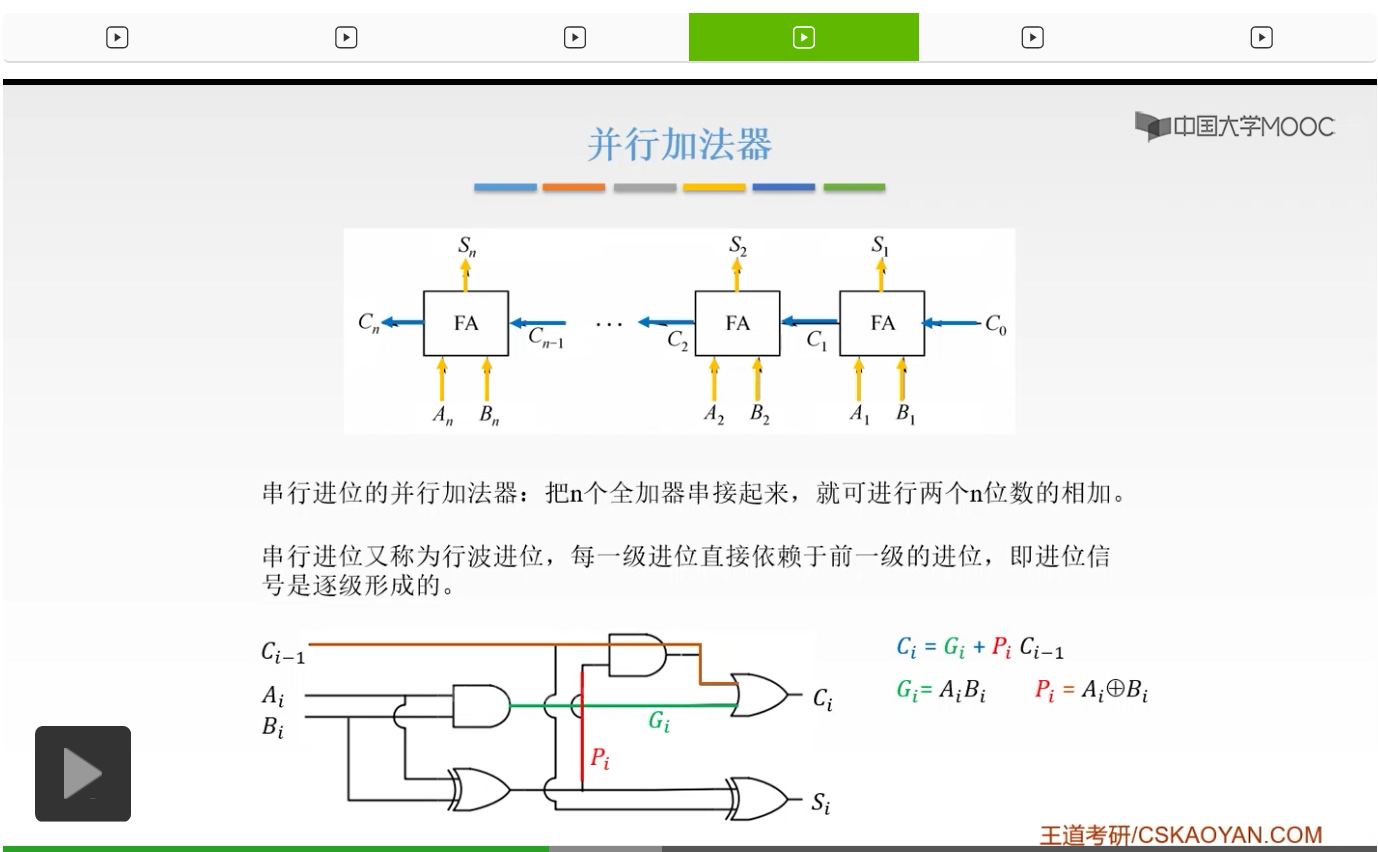
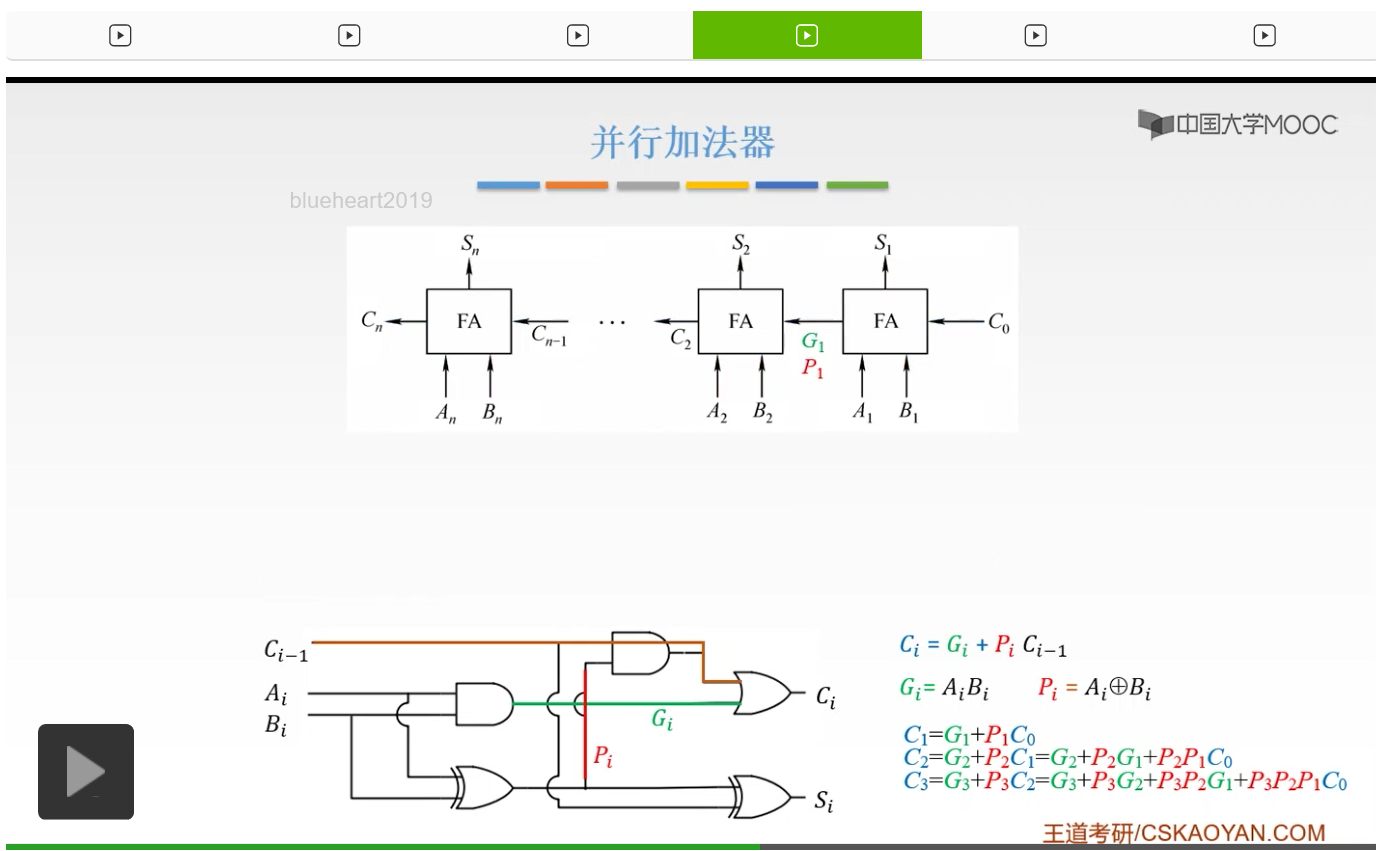
那么这就是并行加法器。我们如果把它串在一起,那么就叫做串行进位的并行加法器。因为这完全是可以实现的,我们产生了一个进位信号,用这个进位信号呢再进入第二个全加器的一个输入信号,而我们前一个全加器的进位信号,当成一个输入信号输入到我们下一个全加器当中。然后把这n个全加器串接起来,我们就可以进行一个n位的数的相加,然后产生我们的结果。

所以呢,我们每一个全加器,接收输入信号,
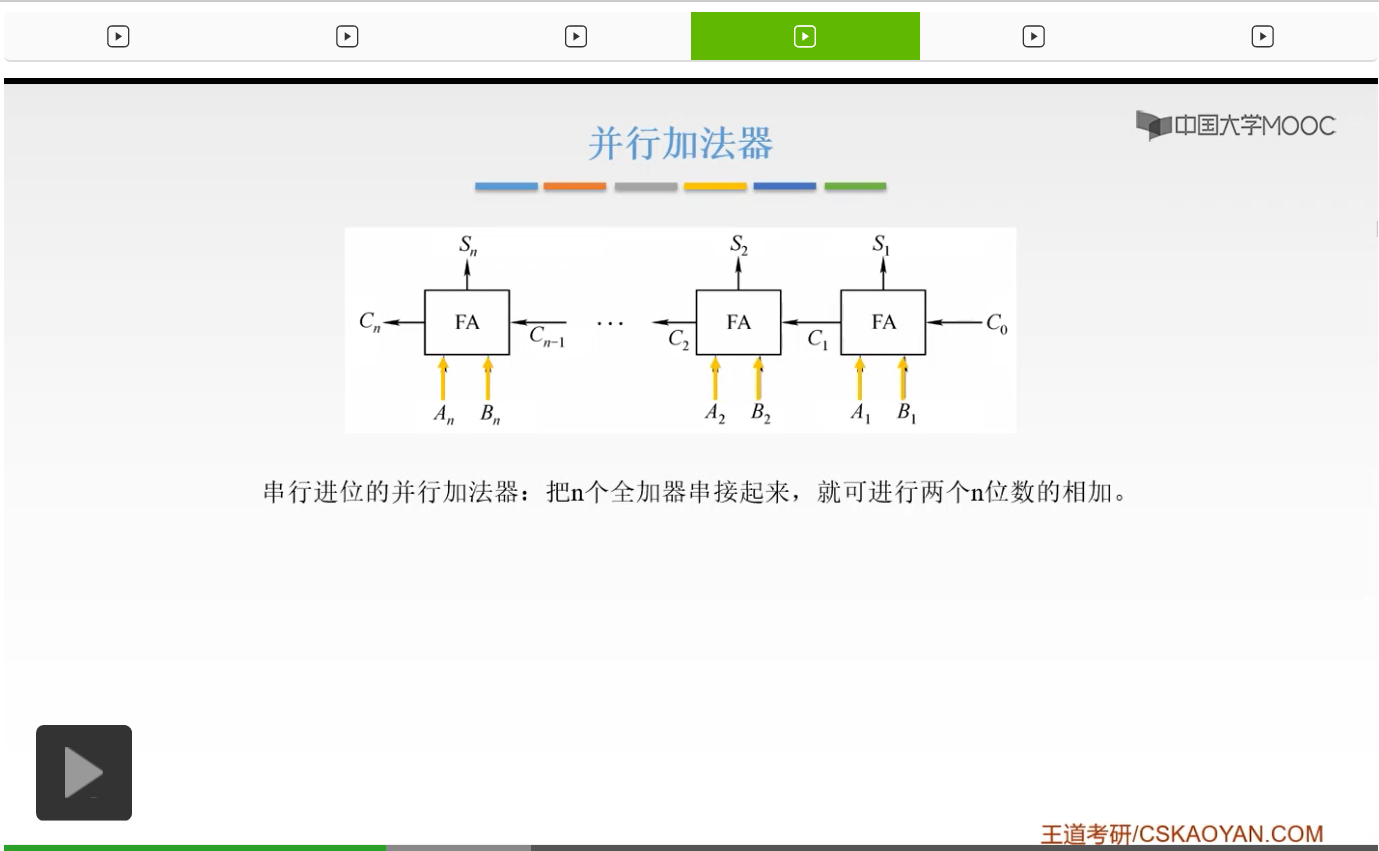
产生结果。
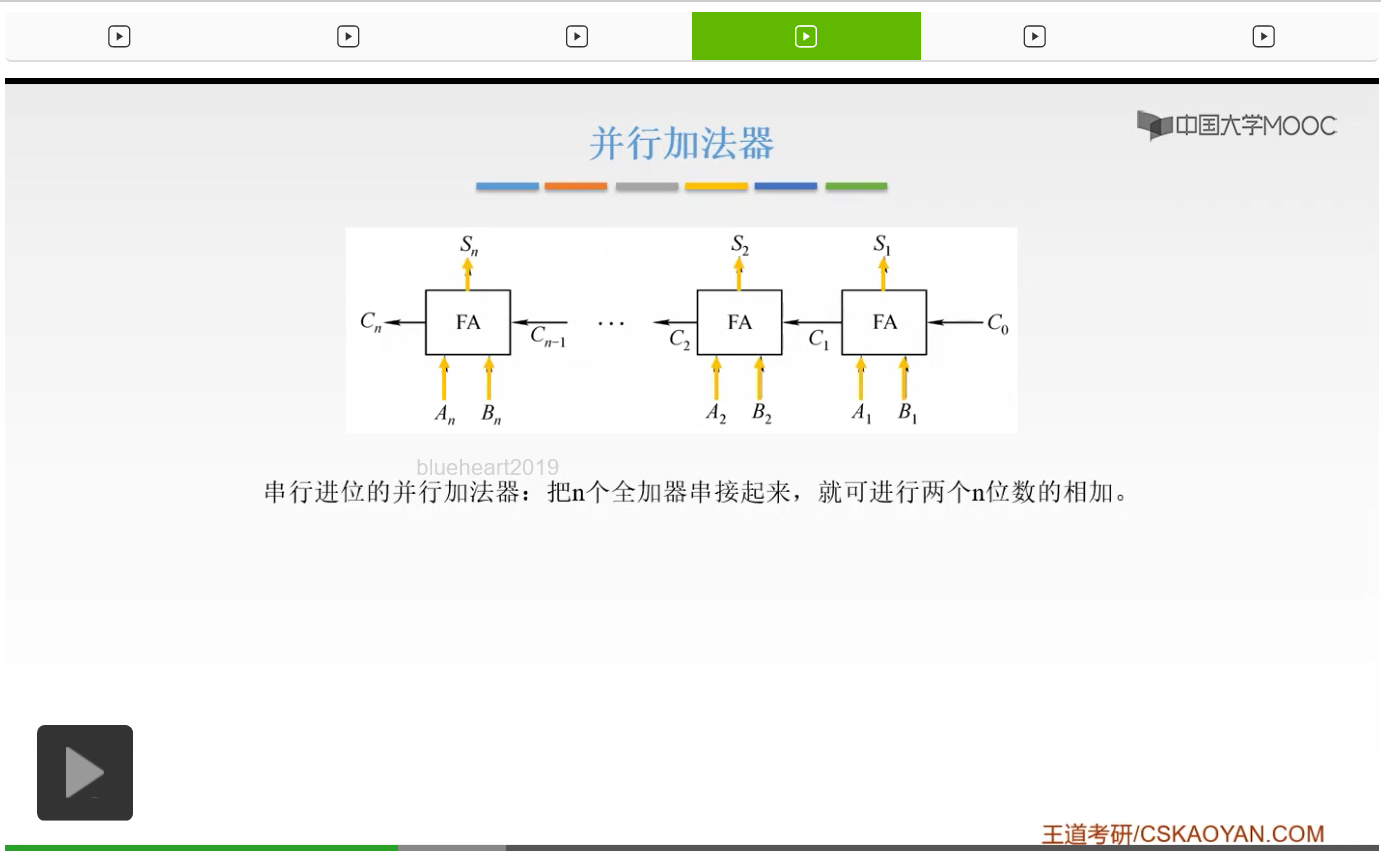
但是它有一个缺点,就是我们的进位信号要从最低的一步一步地传给我们的最高的,最后才能得到一个进位信号。
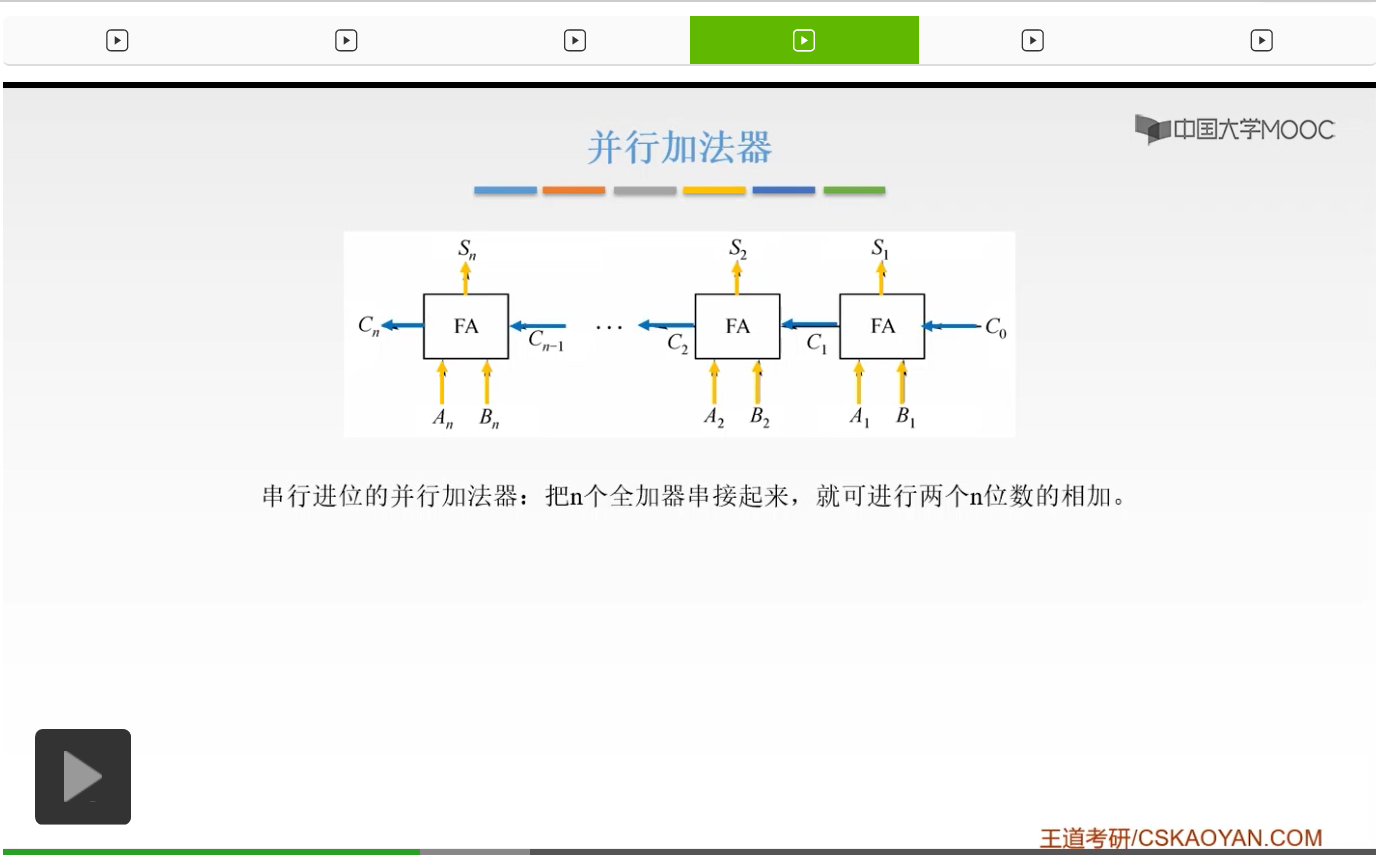
这显然,还是比较慢的。所以呢,这叫做行波进位。因为呢,我们每一级的进位,都直接依赖于前一级的进位,也就是说我们把前一级的进位当成一个输入信号输入进来。所以我们的进位信号呢是逐级产生的,这还是比较慢。那么有没有办法对它进行一个改进呢?就是我们不必等前一个给我提供进位信号,我们就直接能够同时计算出结果,可以吗?
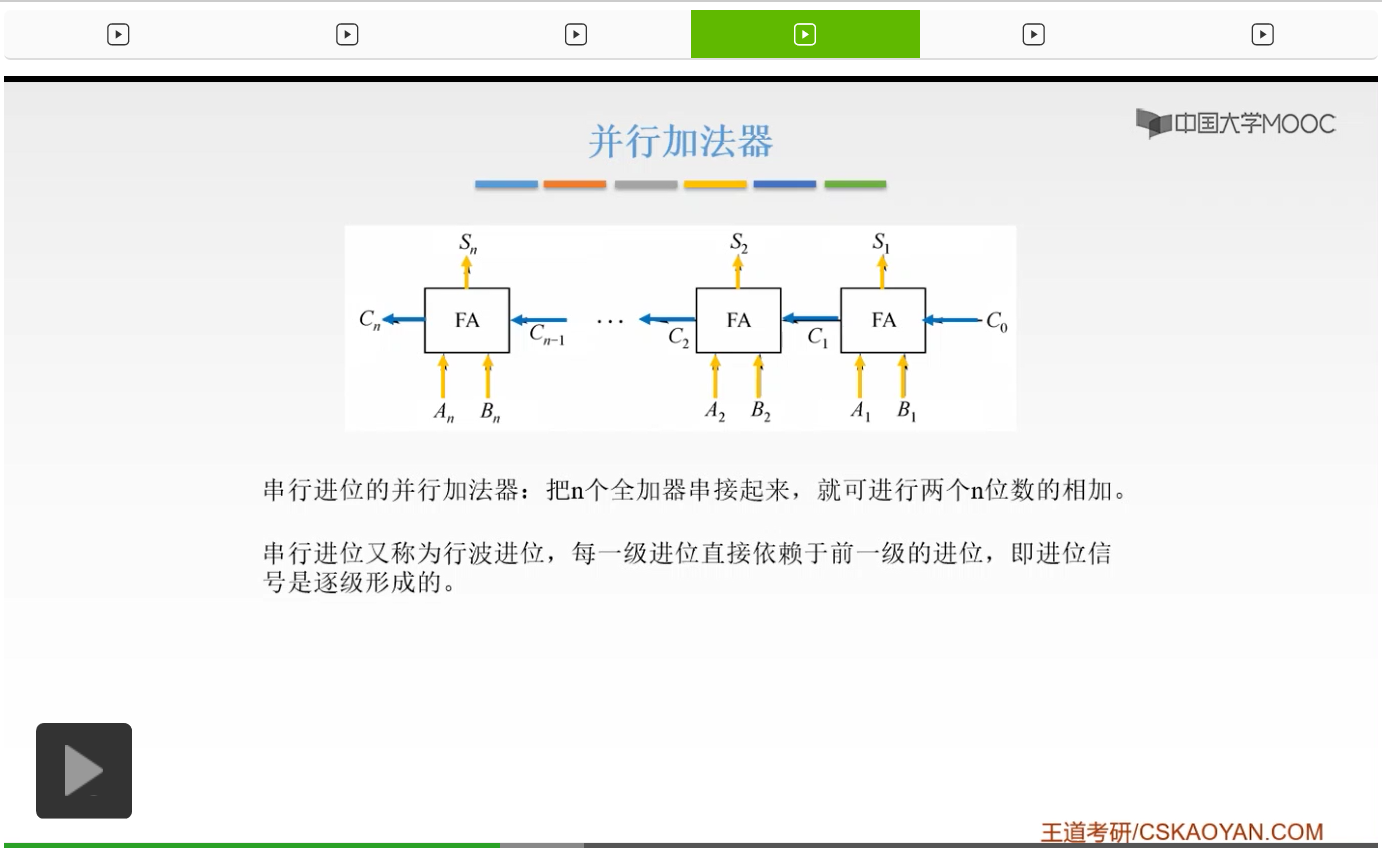
我们来分析一下。我们知道我们的进位信号是怎么产生的。
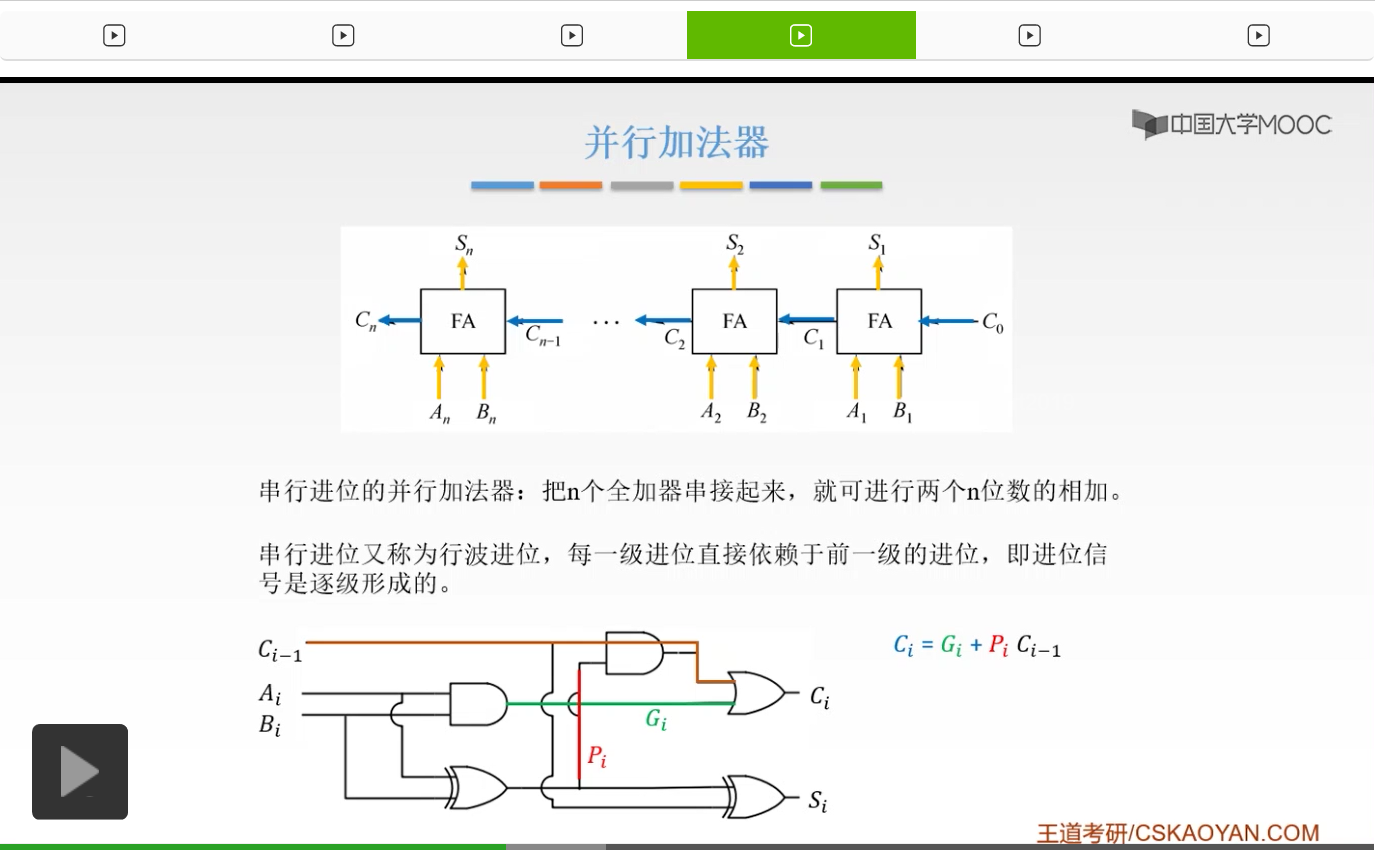
我们之前已经说过了,Gi是Ai乘Bi,Pi呢是Ai异或Bi。也就是说一个是我们本身的这一级的产生的进位,一个呢是接收我们上一级的进位然后再跟我们这一级的输入进行一个判断,产生一个进位,这是一个传递的进位。
我们如果把它展开来,
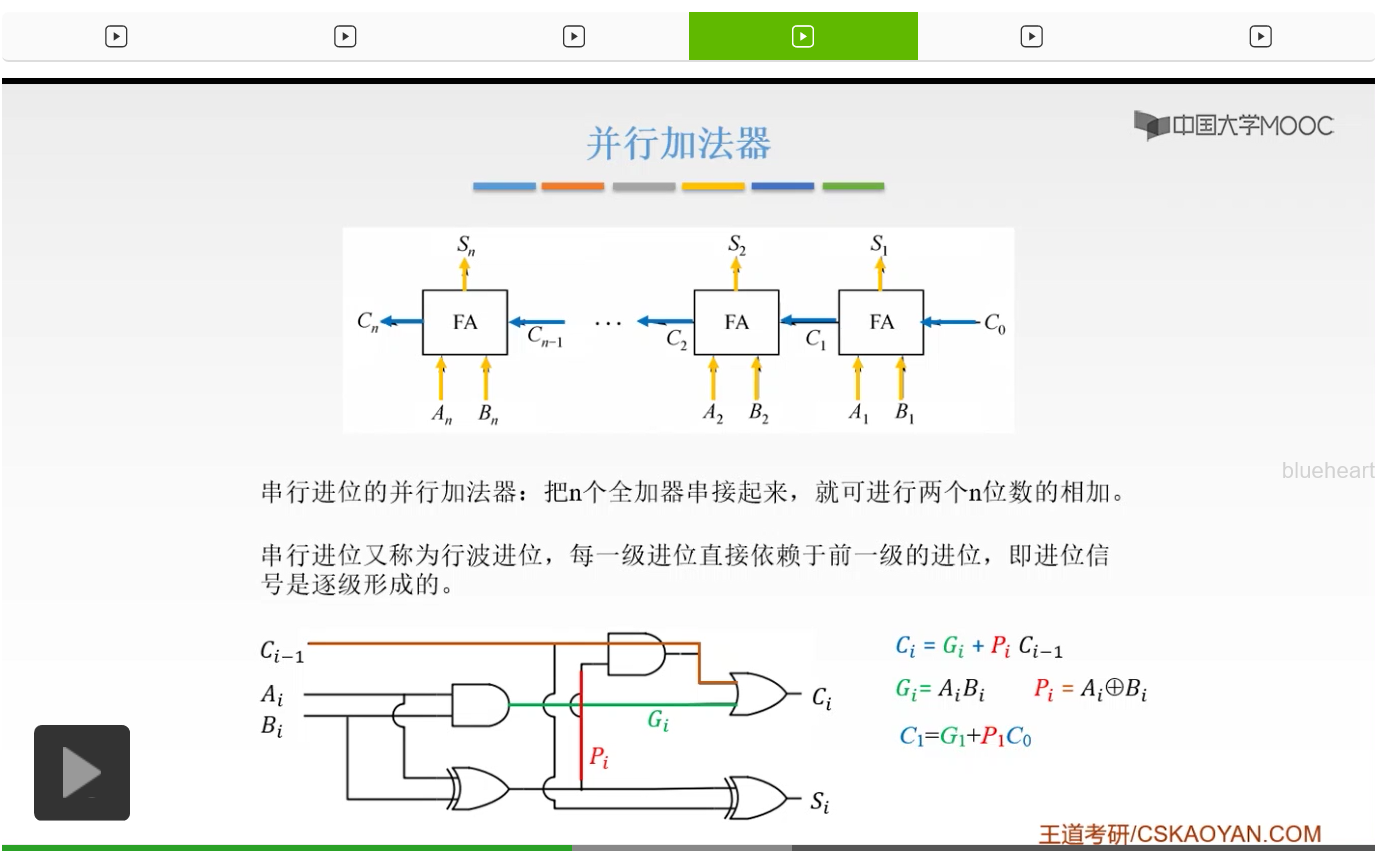
那么C2=G2+P2C1,如果我们把C1替换掉就可以把它替换成P2P1C0。这时候我们就可以看到,C2是不必要依赖C1的,我们只要有输入,只要有C0,我们就可以计算出C2,也就是说我们的每一位都不必要依赖我们的前一位。我们和串行进位是不一样的,串行进位的每一级进位,都直接依赖于前一位的进位。而这时候如果我们把它展开来,我们只要有Ai、Bi和C0就可以了。所以我们的每一级的输出,进位输出啊,仅由我们的Gi、Pi和我们的进位输出C0决定,等于我们的C3。
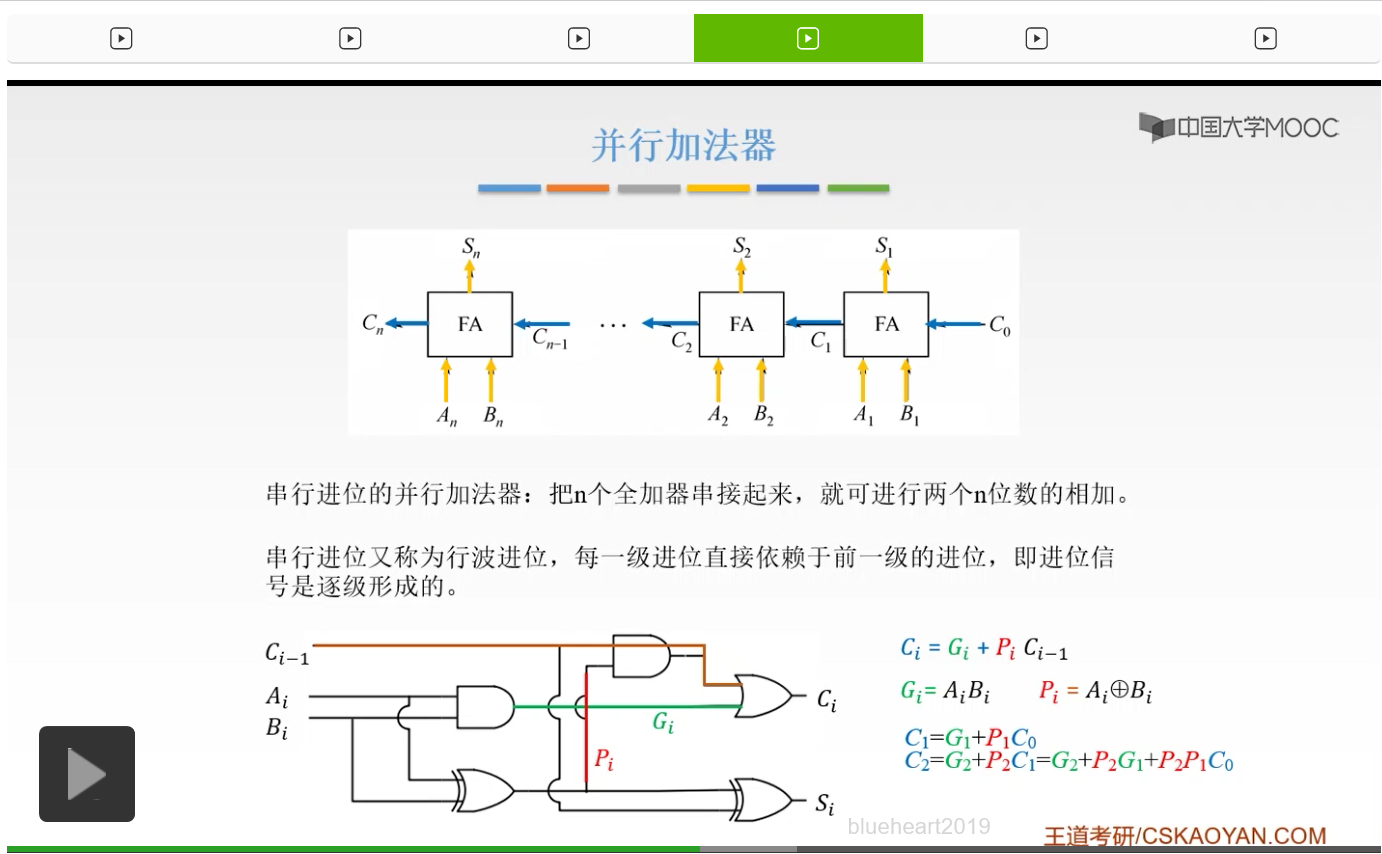
我们C3呢就直接由Gi、Pi和我们的C0决定就可以了而不必要等于C2。所以呢这样的进位方式是比较节省时间的,所以呢我们就通过这样的思想把我们的并行加法器串行进位进行一个改进。
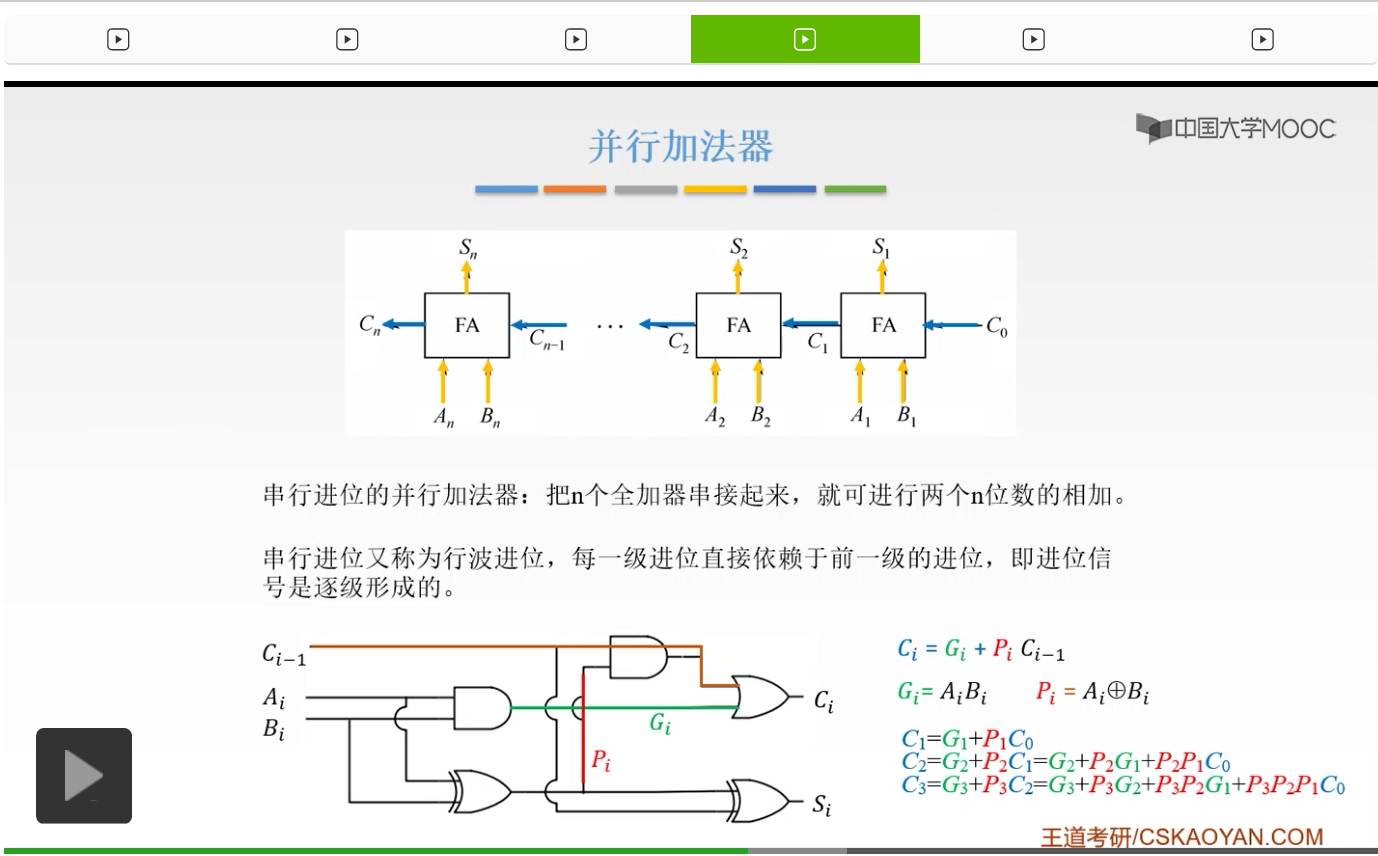
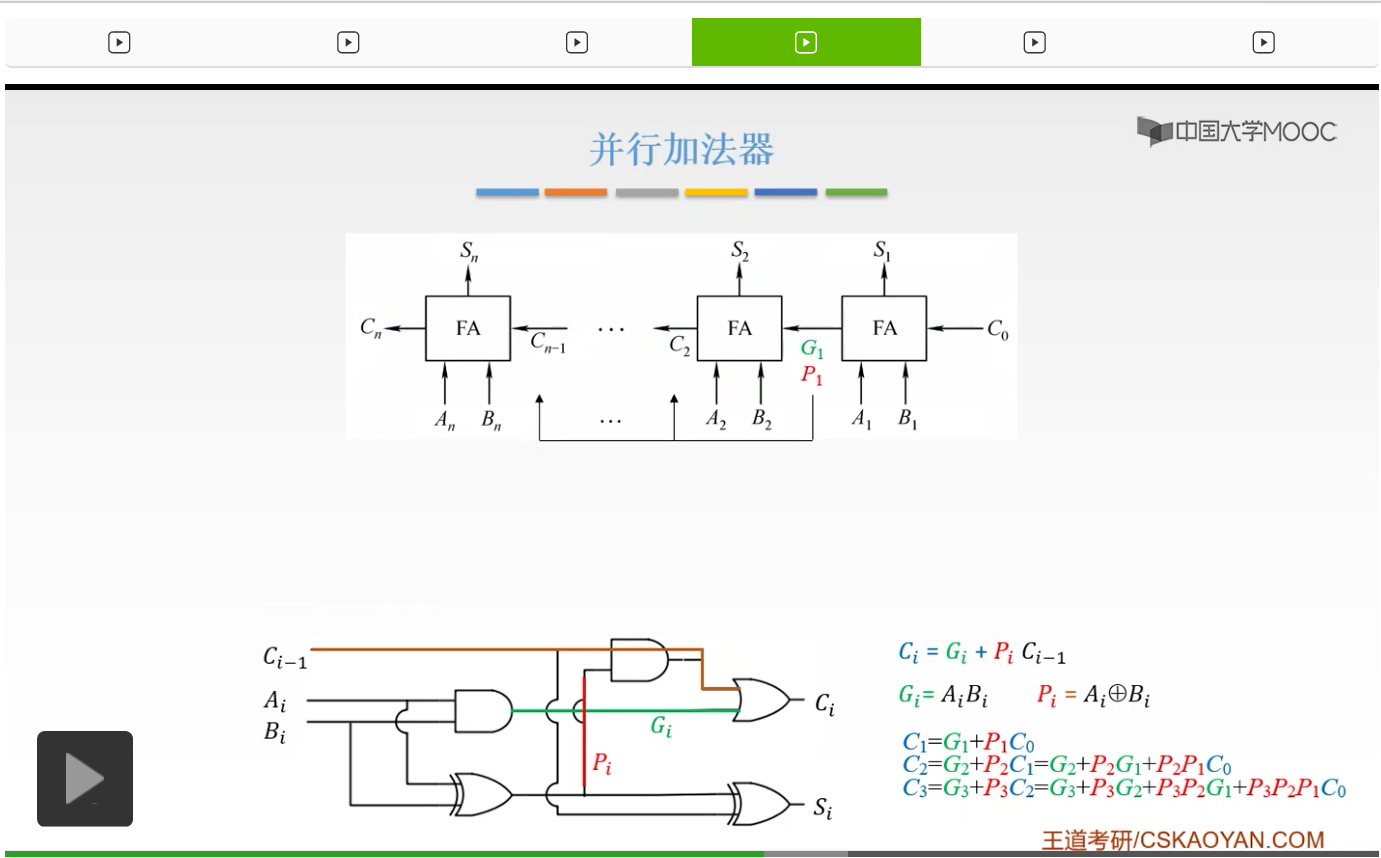
当我们有了G1、P1的时候
我们把G1、P1传递给前面,
然后呢再进行把G2、P2
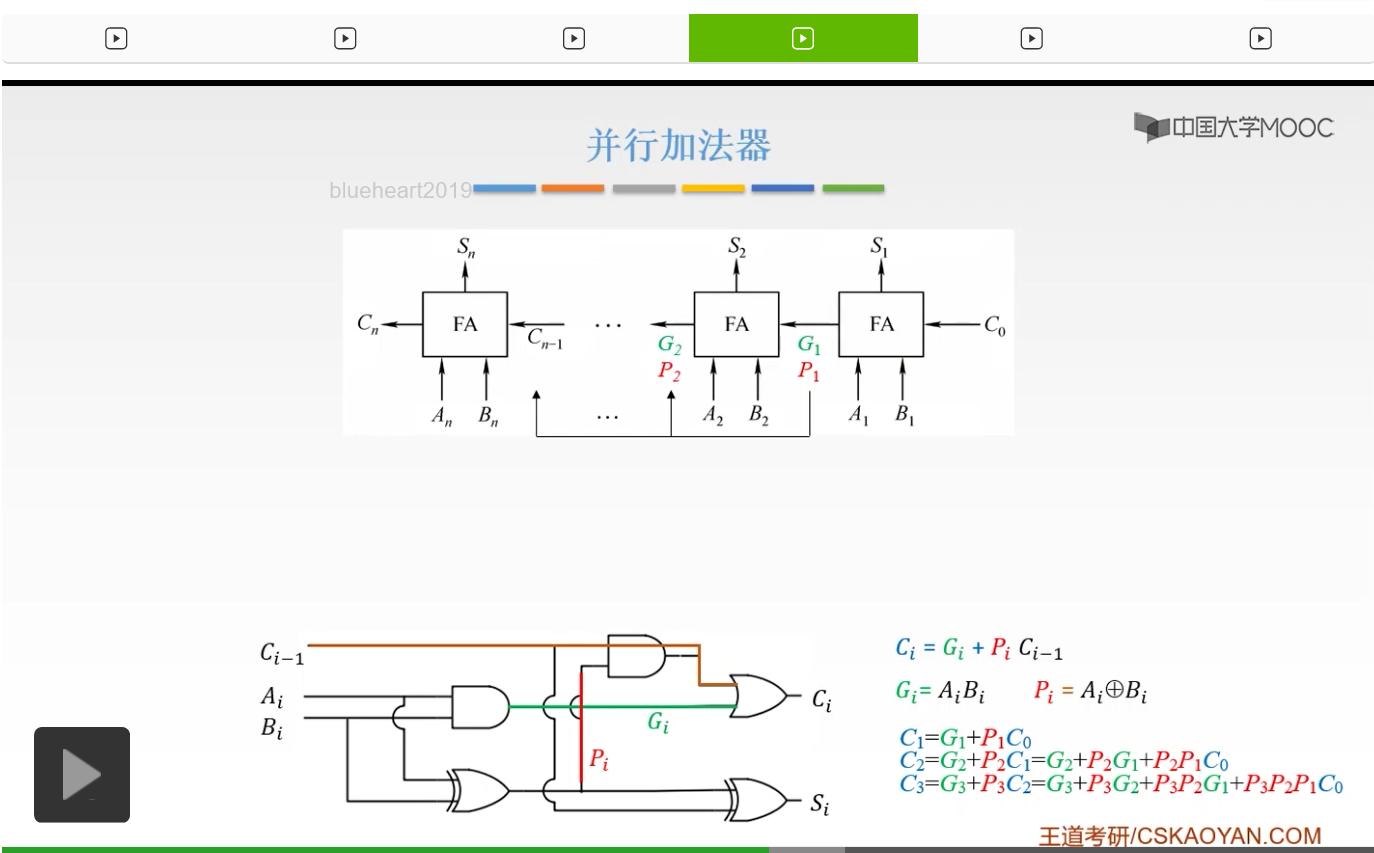
再传递给它前面的东西。
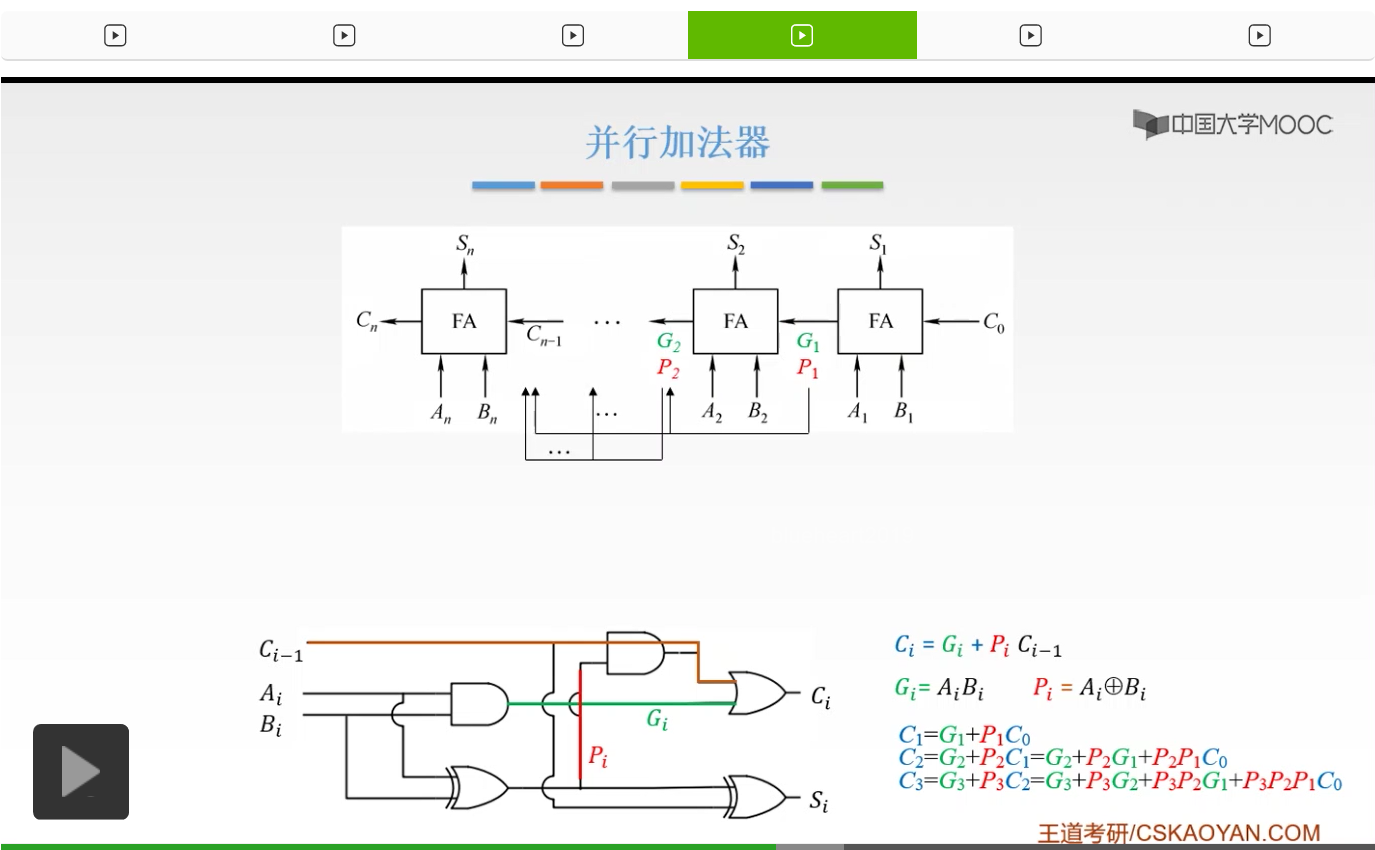
所以我们这时候有了Ai、Bi,
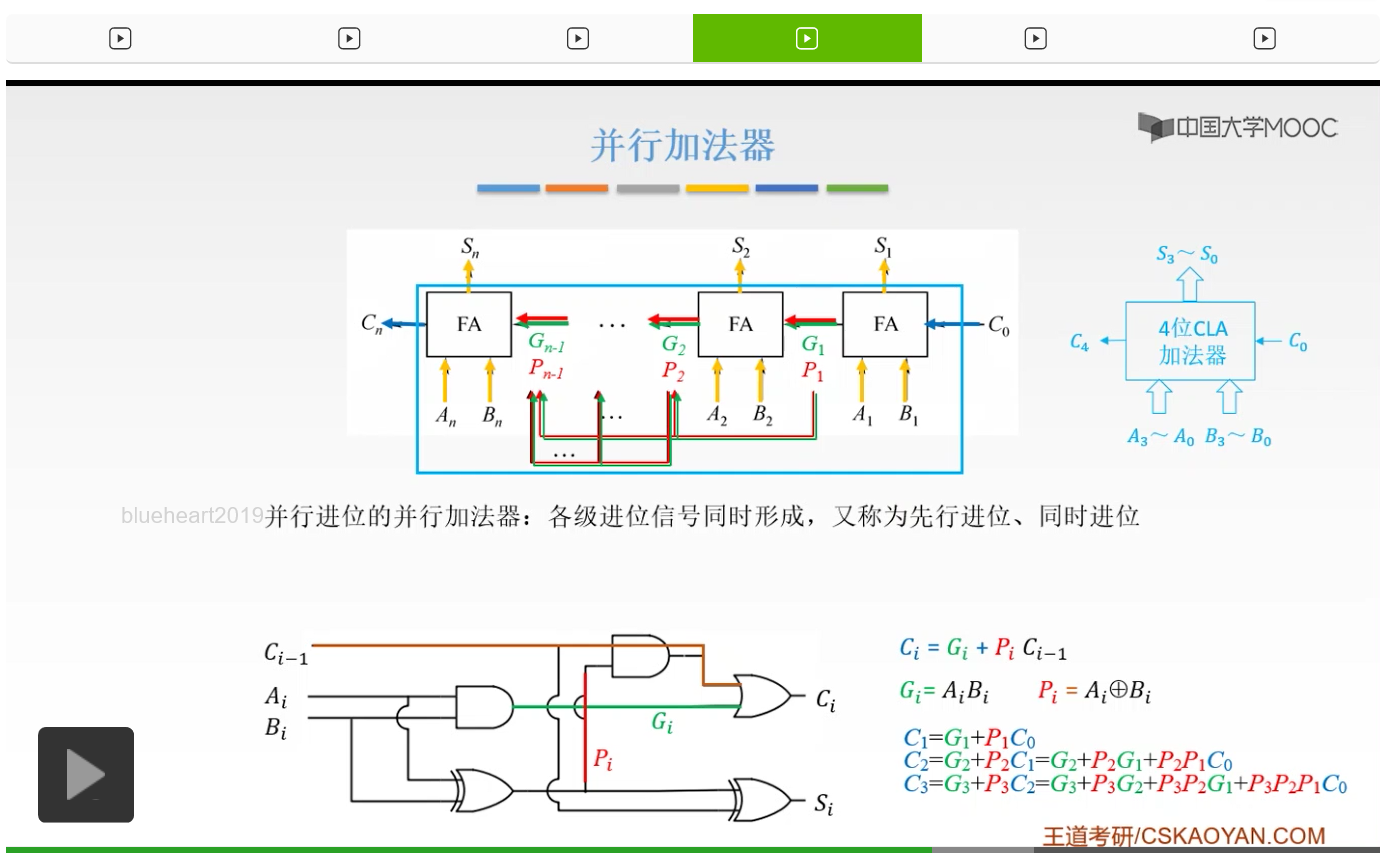
有了C0,我们就完全地直接地计算出了Si和我们的最高位的进位信号Cn。我们不必要等待前一级的进位信号,我们就可以得到我们这一级的进位信号。所以我们所有的进位输出仅由Gi、Pi和我们的最低进位输入C0决定,而不依赖于它的低位的进位信号Ci-1。所以这时候我们的各级的进位输出是可以同时产生的。

那么这样的进位方式呢我们叫做并行进位,并行进位的并行加法器。我们的各级的进位信号是同时形成的,所以呢又把它叫做先行进位和同时进位。

那么如果我们把它封装起来,

就可以得到这样的一个东西。也就是说我们得到了4位的一个并行进位的并行加法器,简称CLA。
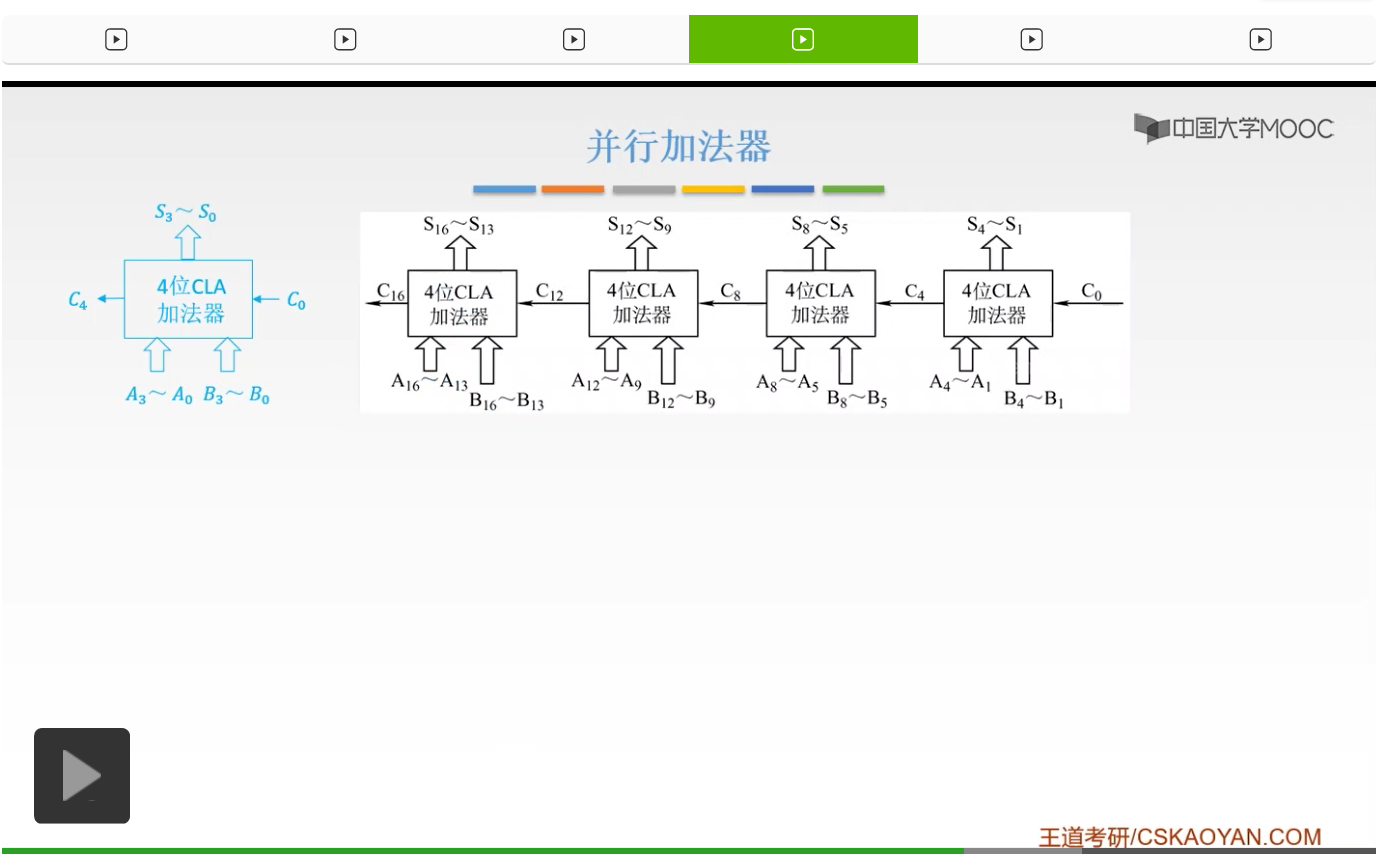
如果我们根据并行进位的并行加法器的这样的思想,

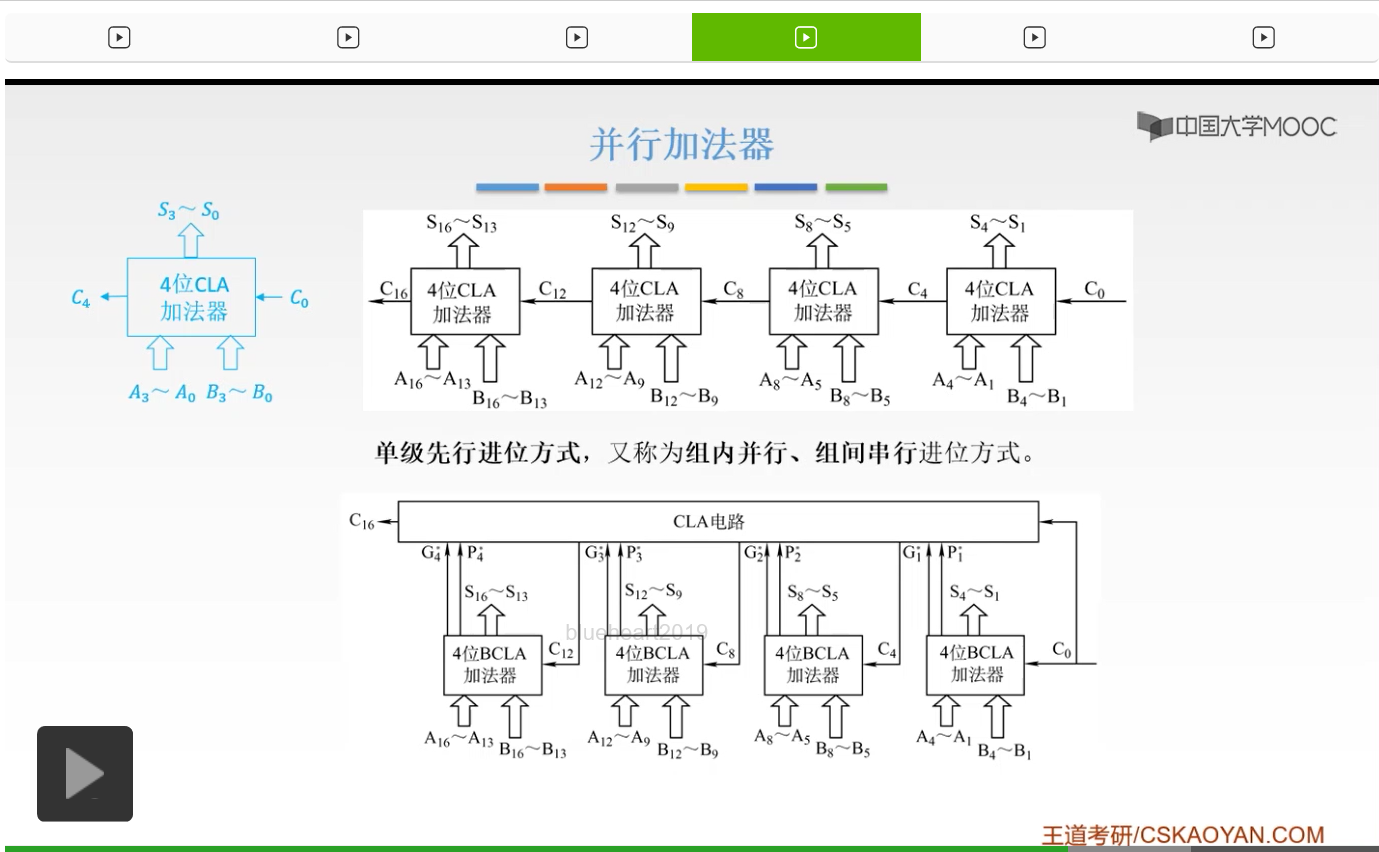
我们把并行加法器也做一个这样的连接,就可以做多位的一个加法器。我们有两种思路,第一种思路,是串行进位的,也就是说我们把我们的CLA再把它进行一个串行的连接,
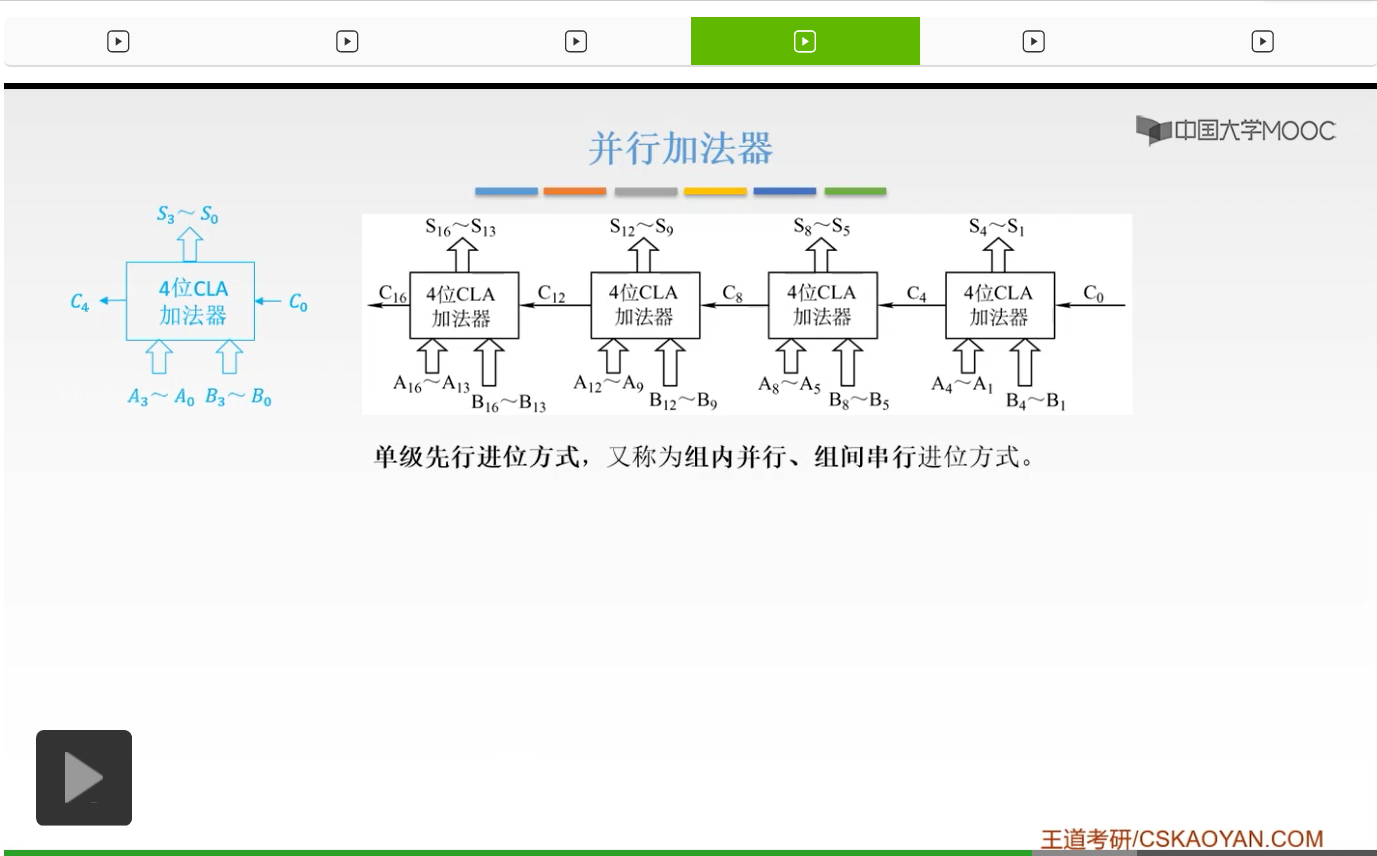
这样呢就得到了一个单级先行的进位方式。那么它是什么呢?它也就是说我们每一个组,每一组它的里面它是并行进位的。因为我们CLA它内部肯定是一个并行进位的一个并行加法器,然后我们再把它进行一个串接,所以它的组间是串行进位的,所以我们把它叫做单级先行的进位方式。
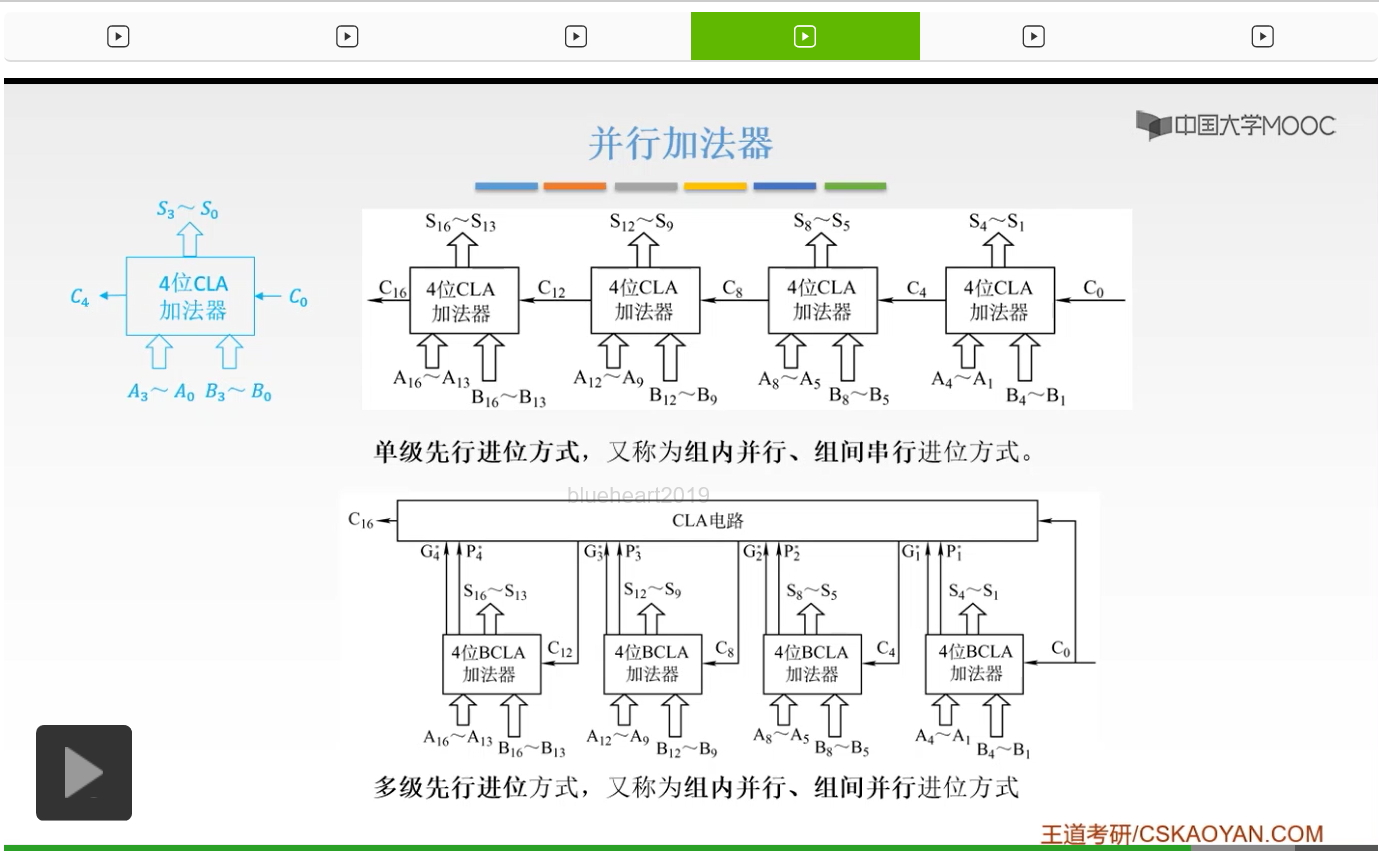
同样的我们也可以把它进行一个并行的连接,就是这样,我们通过一个CLA电路把它进行一个并行连接,
所以我们把它叫做多级先行的一个进位方式。所以它的组内是并行的,它的组间呢还是并行的。所以如果我们把并行加法器再进行一个连接,能够进行更多位的加法的时候,也有两种方式。第一种呢就是我们的组内并行、组间串行,也就是说我们把所有的并行加法器串接起来。同样的呢,我们也可以把它进行一个组间的一个并行,我们通过外面的一个CLA电路,把它也进行一个多级先行的进位方式。那么这就是我们并行加法器的一个用处,因为我们并行加法器这时候只能处理四位的,如果我们想处理更高位的八位的、十六位的话,我们就可以把多个并行加法器再进行一个连接。所以连接方式就有两种,一种呢就是串行的一个连接,一种呢还是通过一个并行的一个连接。
同样的不仅我们的加法器可以进行这样的串接,
我们的ALU芯片也能进行一个连接。这叫做串行的。
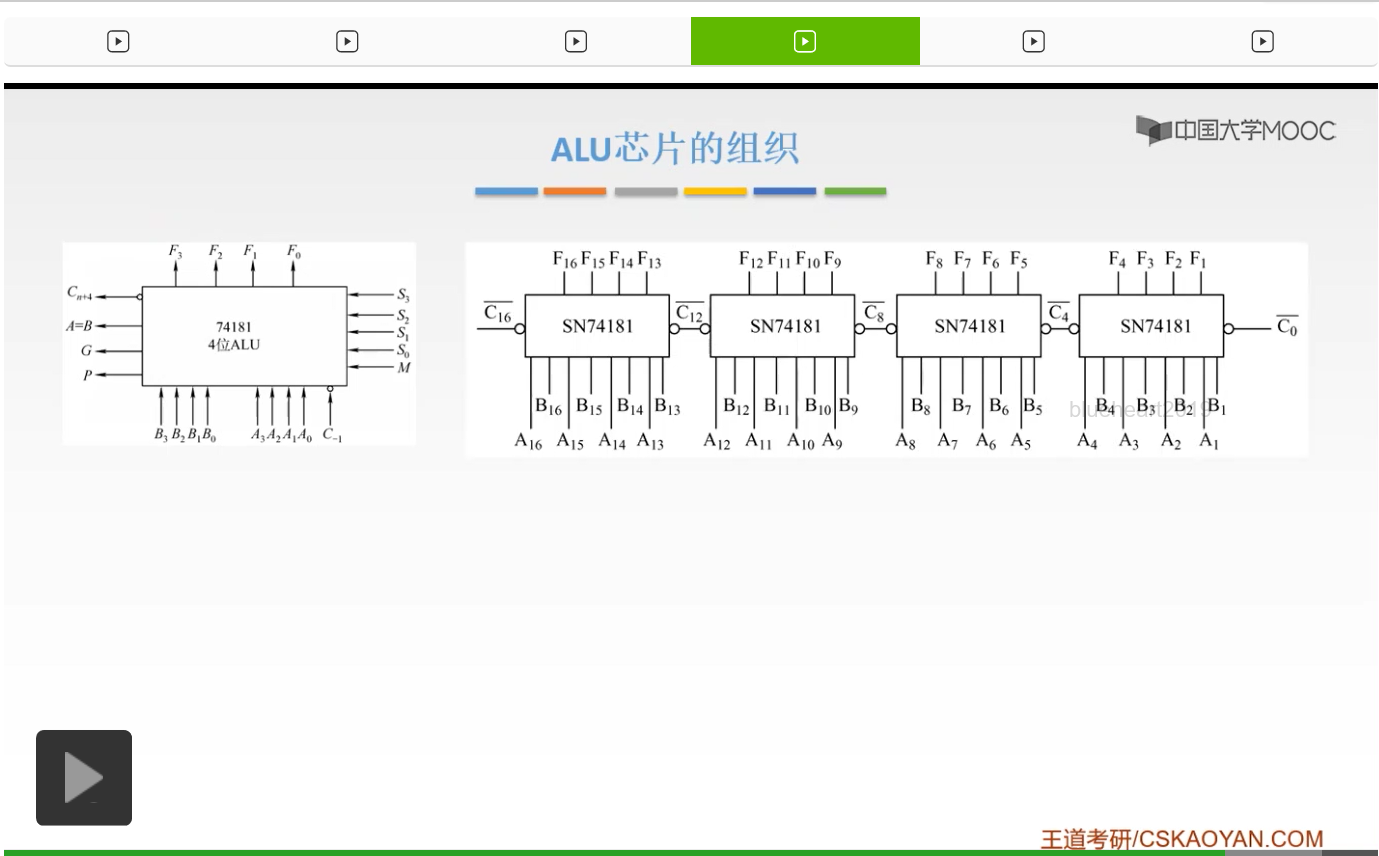
那么这是一个并行的,同样的呢我们还要有一个并行电路。那么我们的思想都是我们的并行加法器的思想,一个是串行的,就是说我们的每一级都要依赖于前一级的进位。一个呢是并行的,也就是说我们不需要依赖前一级的进位,我们只需要依赖Gi、Pi和我们的C0就可以了。用这种方式我们可以对加法器进行一个连接,也可以对芯片进行一个连接。那么本节的内容,就完全地讲完了。注意我们不需要花太多力气在我们的数字电路上面,因为我们要清楚,我们考的是计组,不是考的数电。所以数电只是为了你方便你理解的,我们更重要的是知道它的运行的方式,组成的方式,它组成的一个结构,而不需要纠结太多在它的数字逻辑上面。所以呢我们讲解了串行加法器和并行加法器,以及并行加法器的它的并行进位和串行进位。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号