博弈论专题 1

被博弈论疯狂驲爆，开个博客抢救一下。

2022.7.19

CF1110G Tree-Tac-Toe

感觉这题非常牛逼，写个题解纪念一下。其实就是抄写 Itst 博客。

显然黑色不可能赢。

先假设没有提前涂白的点。

考虑前 $O(1)$ 步白色必胜的情况：

• 存在点的度数 $\geq 4$。

• 存在点的度数 $=3$，并且所连的 $3$ 个点中至少有 $2$ 个非叶子节点。

其余情况，树的形态就只剩下以下三种：

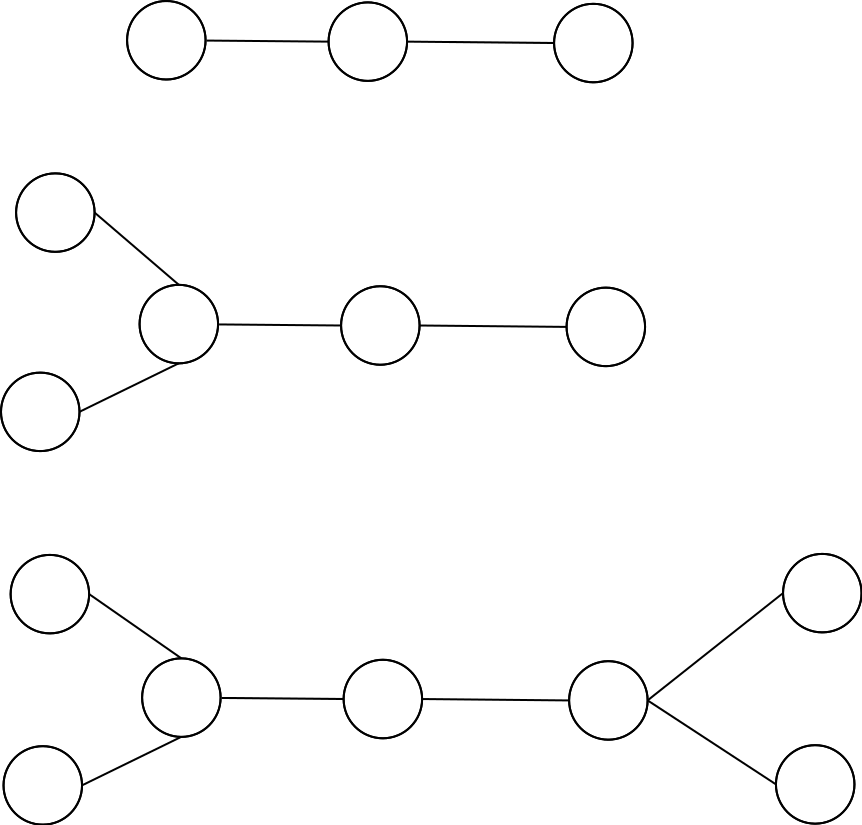
对于第一种，直接黑白染色，必然平局。

对于第二种，同样类似黑白染色，注意好左侧的处理，必然平局。

对于第三种，当且仅当点数个数为奇数时，白色必胜。

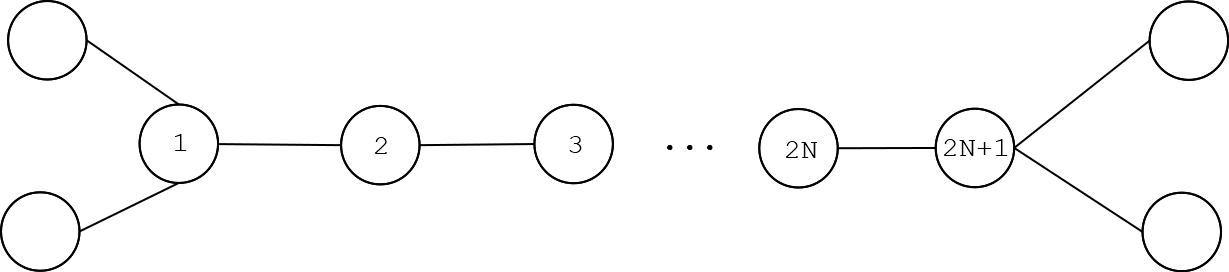
把点编号。白色先手染第 $2$ 个点，黑色一定要染第 $1$ 个点，白色再染第 $4$ 个点，黑色染第 $3$ 个点。最终白色可以染 $2n,2n+1$ 个点，白色必胜。

再考虑有白色涂白的点

把一个在原图中已经涂白的点，拆成 $A,B,C,D$ 四个未涂色的点。

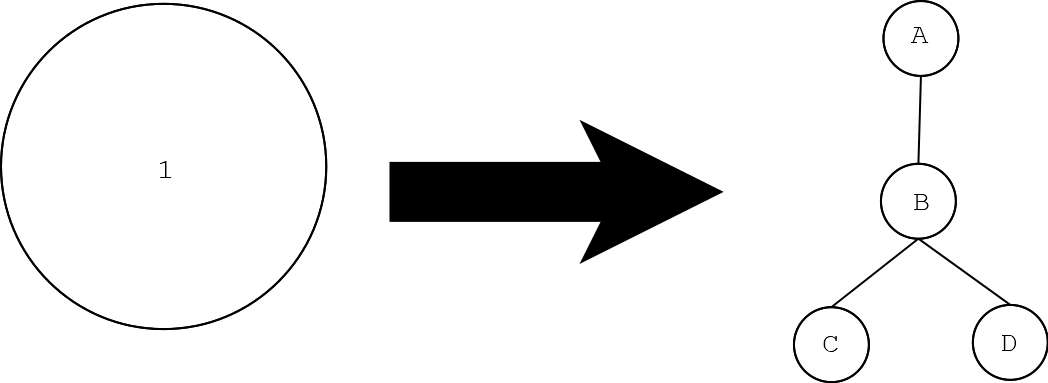
其中原图与 $1$ 号点的连边全都继承在 $A$ 点。

假设游戏开始时直接染白 $A$ 点，此时黑色必须染 $B$ 点。这样，这三个新增加的点对全局没有任何影响。直接用第一种算法搞即可。

CF1076G Array Game

大力猜想，答案只跟奇偶性有关。从后往前 $dp$，设 $f_i$ 表示起点是 $i$ 的状态。如果 $[i+1,i+m]$ 有先手必败态就直接跳，否则就考虑 $a_i$ 的奇偶性，如果是奇数就先手必胜，否则先手必败。

注意到连续的 $m$ 个数里至多有一个先手必败态，对于每个线段树节点 $[l,r]$ 开一个长度为 $2^m$ 的数组（这是壬能想到的🐎艹），$g_S$ 表示当 $[r+1,r+m]$ 的状态为 $S$ 时，$[l,l+m-1]$ 的状态。合并可以 $O(2^m)$ 解决。

其他的操作都是线段树的基本操作了。

CF1091H New Year and the Tricolore Recreation

显然只跟差值有关。一开始我以为同一行的两个值不是独立的，打了个 $[0,15] \times [0,15]$ 的表，找到了一个非常棒的规律。我非常兴奋，打了个更大的表，发现规律没了 /fn。

发现同一行的两个值其实也是独立的，并且 SG 函数值域很小，记录 $w$ 的是否在 $SG_i$ 的 $mex$ 里，暴力用 bitset 驲即可。

CF725F Family Photos

看错题自闭了一中午 /ll。

• $a_1+b_1 < a_2+b_2,a_1 > b_2$ ，对答案的贡献是 $a_1 - b_2$
• $a_1 + b_1 < a_2 + b_2 , a_ 2 < b_1$ ，对答案的贡献是 $-(b_1 - a_2 )$
• $a_1 + b_1 \geq a_2 + b_2$：把一个卡牌的权值变成 $a_i + b_i \over 2$，答案加上 $a_1 + a_2 \over 2$。再贪心选卡即可。

CF838C Future Failure

记 $a_i$ 为字母 $i$ 的出现次数。

发现当排列方式个数为偶数时，先手必胜。用数学归纳法证明，显然在 $\sum a_i=1$ 时成立。对于 $\sum a_i > 1$，如果删除一个字母可以到先手必败态，先手进行转移。否则就一直重排。

当排列个数为奇数时，每次只能长度减一。即当 $\sum a_i$ 为奇数时先手必胜。否则先手必败。

考虑计算在 $n = \sum a_i$ 为偶数时，排列个数为奇数的数量。对于 $i!$，含 $2$ 的幂次是 $\sum\limits _{x=1} \lfloor {i \over 2^x }\rfloor$。

可以得到

$$\sum_{x=1} \lfloor { n \over 2^x} \rfloor = \sum_i \sum_{x=1} \lfloor { a_i \over 2^x} \rfloor$$

因为

$$\lfloor {a \over x}\rfloor + \lfloor {b \over x}\rfloor \leq \lfloor {a+b \over x}\rfloor$$

所以

$$\forall x,\lfloor {n \over 2^x}\rfloor = \sum_{i} \lfloor {a_i \over 2^x}\rfloor$$

也就是说把 $n$ 拆成二进制，如果为 $0$，说明所有 $a_i$ 这一位都为 $0$。否则恰有一个 $a_i$ 这一位为 $1$。设 $dp_{i,S}$ 表示当前解决了前 $i$ 个数，剩余集合 $S$，$\prod {1 \over a_i}$ 的值。直接转移是 $O(k 3^{log_2n})$ 的，会被卡。发现转移是个子集卷积的形式，复杂度就对了（然而我还是差点被卡）。

2022.7.20

一天就两题，不愧是我 /kx。

CF1610I Mashtali vs Atcoder

$k=1$ 的情况是 AGC017D。对于 $k\geq 2$ 的情况，把两个黑点中间的点全都标黑。定义两个黑点中间的边是黑边（白边同理），一个黑点和一个白点之间的边是灰边。那么答案就是所有灰边的 SG 函数 xor 上黑边的奇偶性。

证明分成两个部分，第一个部分是当前情况不能走到 SG 函数相同的情况。按边的颜色分类讨论，证明是容易的。然后可以把每条黑边独立看作一个整体，每条灰边连接的一个黑点和一个白子树看作一个整体，按照 SG 函数定义证明。

LOJ3114 「SDOI2019」移动金币

SDOI2019D2T2？怕个锤子，看我直接切穿。 事实证明我还是 too naive 了。

发现并不会判先手还是后手必胜，去学了个叫阶梯 Nim 的东西，简单地说就是博弈结果仅跟奇数位的 Nim 游戏结果有关。然后发现做完了。