51nod1355 斐波那契的最小公倍数

题目描述

斐波那契数列定义如下：

 

F(0) = 0 F(1) = 1
F(n) = F(n-1) + F(n-2)

 

给出n个正整数a1, a2,...... an，求对应的斐波那契数的最小公倍数，由于数字很大，输出Mod 1000000007的结果即可。

例如：1 3 6 9, 对应的斐波那契数为：1 2 8 34, 他们的最小公倍数为136。

题解

参考

我们都知道min-max容斥。

对于gcd和lcm的关系，我们也可以认为这是一个指数取交集和指数取并集的操作，所以有

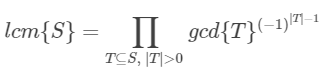
然后关于斐波那契数有一个定理：

于是就有：

 

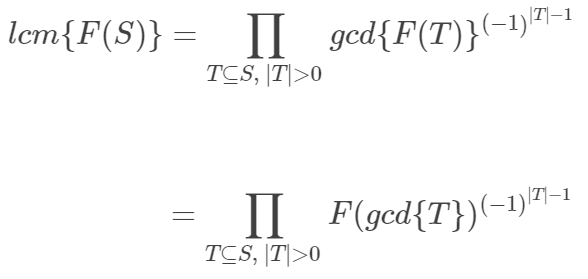
然后考虑神奇操作，我们设一个G函数。

然后原式就变成：

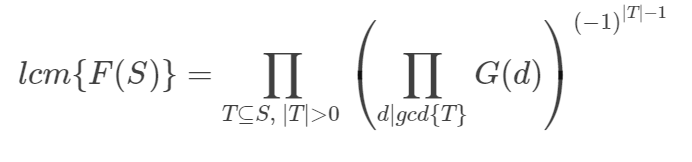
考虑枚举d：

然后对于指数上的东西，还有一个结论：

至于为什么是1，证明也是容斥。

因为每个元素都小于1e6，所以我们可以直接对每个元素算贡献了。

代码

#include<iostream>
#include<cstdio>
#define N 1000009
using namespace std;
typedef long long ll;
const int mod=1000000007;
ll g[N],a[N],ans=1,maxn;
bool vis[N];
int n;
inline int rd(){
    int x=0;char c=getchar();bool f=0;
    while(!isdigit(c)){if(c=='-')f=1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return f?-x:x;
}
inline ll power(ll x,ll y){
    ll ans=1;
    while(y){if(y&1)ans=ans*x%mod;x=x*x%mod;y>>=1;}
    return ans;
}
int main(){
    n=rd();
    for(int i=1;i<=n;++i)a[i]=rd(),maxn=max(maxn,a[i]),vis[a[i]]=1;
    g[1]=1;
    for(int i=2;i<=maxn;++i)g[i]=(g[i-1]+g[i-2])%mod;
    for(int i=1;i<=maxn;++i){
        ll ni=power(g[i],mod-2);
        for(int j=i*2;j<=maxn;j+=i)g[j]=g[j]*ni%mod;
    }
    for(int i=1;i<=maxn;++i){
        bool tag=0;
        for(int j=i;j<=maxn;j+=i)if(vis[j]){tag=1;break;}
        if(tag)ans=ans*g[i]%mod;
    }
    cout<<ans;
    return 0;
}