dijkstra算法

Dijkstra算法

求解问题

• 从某点出发到其它点的图的最短路径
• 从其它点出发到某一点的最短路径
• 从某点到某点的最短路劲

求解方式

算法思路（通俗）

1. 从一点出发，找到其相邻的顶点，记录到这些点的距离（同时记录其前驱）。
2. 在接下来的点中找到数值最小的点作为新一轮的点。
3. 重复步骤1，若发现距离更近则更新最短路径，否则不更新。
4. 直到所有点被访问完全结束。

​ 若有如图所示的无向有权图：

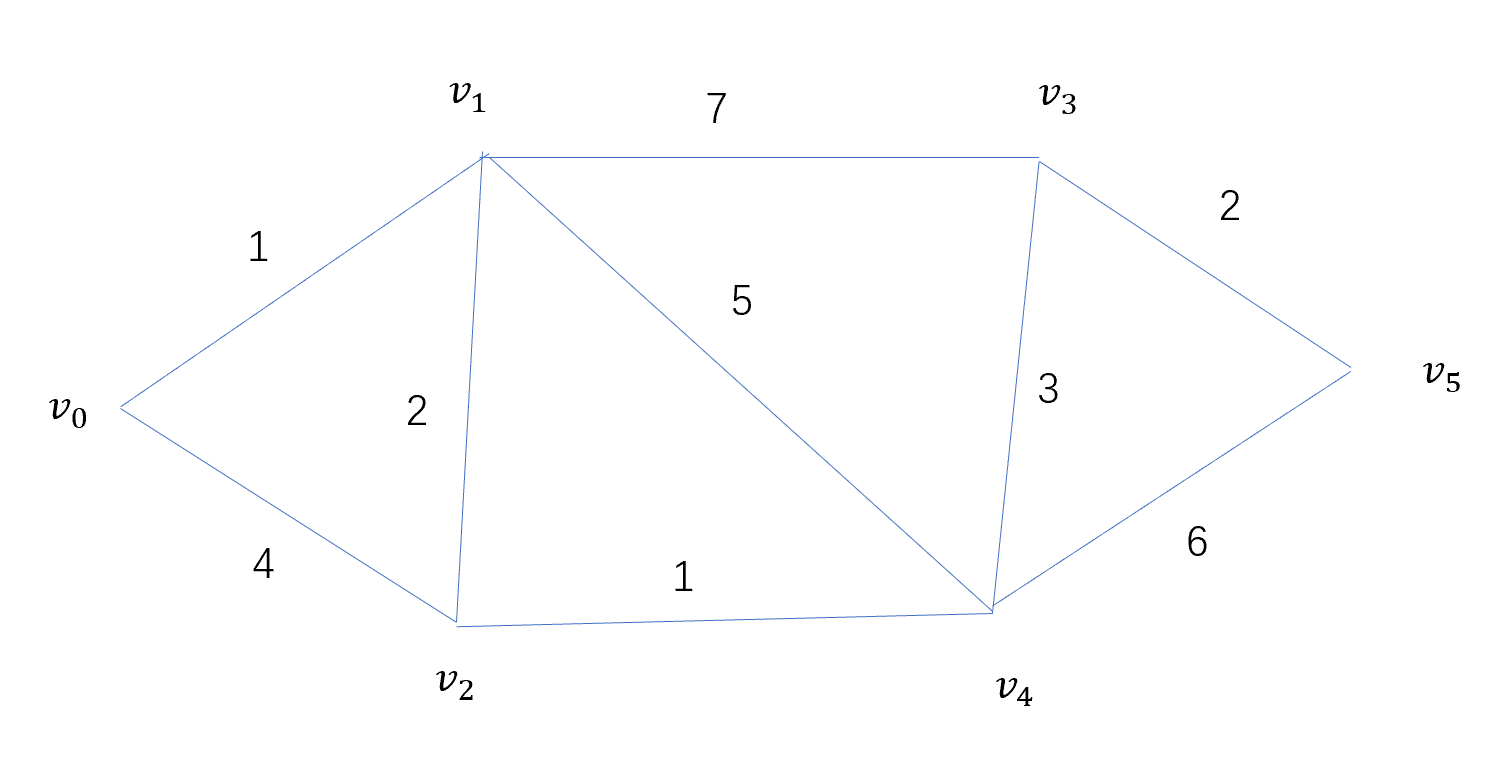
​ 则从\(v_0\)出发的最短路径如下表：

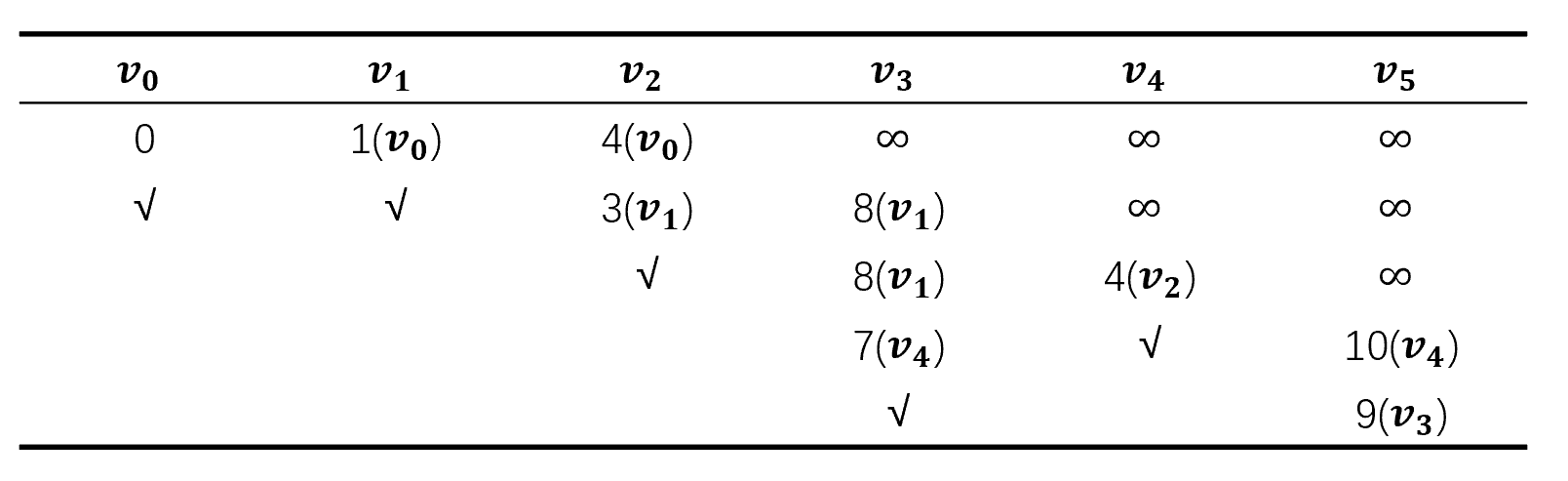
代码思路

1. 首先定义无穷INF，最大点数MAXV，图的邻接矩阵G[MAXV][MAXV]，最短路径d[MAXV]，以及访问对象记录vis[MAXV]。
2. 先将图的邻接矩阵初始化每条边的权值为无穷，再按照图进行存储。
3. 定义Dijkstra()函数
   • 首先将最短路径d[MAXV]初始化为无穷，起点赋值0；
   • 第一层循环需要遍历所有的点，定义每轮研究的点u，以及最小值MIN；
   • 第二层循环再次遍历所有的顶点，找到没有访问过且路径最小的点，更新u和min；
   • 若u==-1即不存在新的点则访问结束退出循环，否则记录该点被访问；
   • 循环遍历所有顶点找到与u相邻的其他点（即该点未被访问过，邻接矩阵对应地权值不为无穷（相邻）），若是u的路径加上其到相邻点的路径之和小于相邻点原有的路径大小，则更新该路径。(关键步骤)

​ 下面通过代码模拟上述的图。

• 问题引入：

  ​ 对于一个无向有权图，先给定图的顶点数n，接下来若干行，每行三个数，a，b，w，表示边的两个端点（a，b）和边权w，当a=0,b=0,w=0时结束。最后一行给出所要求的最短路径起点st，和终点ed，求最短路径。

• 输入：

6
0 1 1
0 2 4
1 2 2
1 3 7
1 4 5
2 4 1
3 4 3
3 5 2
4 5 6
0 0 0
0 5

• 输出：

9

• 程序设计:

#include<bits/stdc++.h>
using namespace std;
const int INF=1e9;	//无穷 
const int MAXV=1010;	//最大点数 
int n;	//n个点 
int G[MAXV][MAXV]; 	//邻接矩阵 
int d[MAXV];	//最短路径 

bool vis[MAXV]={false};	//访问对象 

void Dijkstra(int s){
	fill(d,d+MAXV,INF);		//初始化最短路径 
	d[s]=0;	//起点为0 
	for(int i=0;i<n;i++){
		int u=-1;	//未访问过且路径最短的顶点 
		int MIN=INF;
		for(int j=0;j<n;j++){
			if(vis[j]==false&&d[j]<MIN){
				u=j;
				MIN=d[j]; 
			}
		}
		if(u==-1) return; //不存在新的点,访问结束退出循环
		vis[u]=true;	//记录该点被访问
		for(int v=0;v<n;v++){
			if(vis[v]==false&&G[u][v]!=INF&&d[u]+G[u][v]<d[v]){
				d[v]=d[u]+G[u][v];	//更新路径 
			}
		} 
	}
}

int main(){
	cin>>n;
	int a,b,w;
	fill(G[0],G[0]+MAXV*MAXV,INF);	//初始化邻接矩阵 
	while(1){	//记录图的邻接矩阵 
		cin>>a>>b>>w;
		if(a==0&&b==0&&w==0) break;
		G[a][b]=w,G[b][a]=w;	
	}
	int st,ed;
	cin>>st>>ed;
	Dijkstra(st);
	cout<<d[ed]<<endl;
	return 0;
}

典例分析

小明的难题