二分法

需求

# 需求：有一个按照从小到大顺序排列的数字列表
#      需要从该数字列表中找到我们想要的那一个数字
#      如何做更高效？

nums = [-3,4,7,10,21,43,77,89]
find_num = 77 # 代表本次要查找的数字

常规方法

# 需求：有一个按照从小到大顺序排列的数字列表
#      需要从该数字列表中找到我们想要的那一个数字
#      如何做更高效？

nums = [-3,4,7,10,21,43,77,89]
find_num = 77 # 代表本次要查找的数字

count = 1
for i in nums:
    if i == find_num:
        print("找到了,查找次数为:{}次".format(count))
        break
    count += 1
else:
    print("没找到，共查找了:{}次".format(count))

# 平常的做法，只能靠运气来找。如果被排列的数值在整个列表的后面，刚好列表又十分庞大，
# 那么花费的时间是非常久的。
# ==== 执行结果 ====
"""
找到了,查找次数为:7次
"""

while循环实现二分法

# 需求：有一个按照从小到大顺序排列的数字列表
#      需要从该数字列表中找到我们想要的那一个数字
#      如何做更高效？

nums = [-3, 4, 7, 10, 21, 43, 77, 89]
find_num = 77  # 代表本次要查找的数字
left = 0
right = len(nums) - 1  # 代表列表索引范围

count = 1
while (left <= right):
    mid = (left+right) // 2  # 代表列表中间索引
    if find_num < nums[mid]:
        right = mid - 1
    elif find_num > nums[mid]:
        left = mid + 1
    elif find_num == nums[mid]:
        print("找到了，查找次数为:{}次".format(count))
        break
    else:
        print("没找到，查找次数为:{}次".format(count))
    count += 1

# ==== 执行结果 ====
"""
找到了，查找次数为:3次
"""

递归实现二分法

# 需求：有一个按照从小到大顺序排列的数字列表
#      需要从该数字列表中找到我们想要的那一个数字
#      如何做更高效？

nums = [-3, 4, 7, 10, 21, 43, 77, 89]
find_num = 77  # 代表本次要查找的数字
count = 1


def binary_search(find_num, li):
    global count  # 传入计数器
    count += 1
    if not len(li):  # 判断新切分的列表长度
        print("没找到,查找次数为:{}次".format(count))
        return

    li.sort()  # 进行排序
    mid_index = len(li) // 2
    mid_val = li[mid_index]

    if find_num > mid_val:
        new_l = li[mid_index+1:]
        res = binary_search(find_num, new_l)
        return res  # 由于是递归，所以地推阶段时要每一层都返回

    elif find_num < mid_val:
        new_l = li[:mid_index]
        res = binary_search(find_num, new_l)
        return res

    else:
        print("找到了，查找次数为:{}次".format(count))
        return find_num


binary_search(find_num, nums)

# 二分法，传入的列表必须是有序的。每次查找都先拿到中间值，
# 判断中间值与查找值的大小。如果查找值较大则切分右边列表，继续拿中间值
# 重复比较步骤...
# ==== 执行结果 ====
"""
找到了，查找次数为:3次
"""

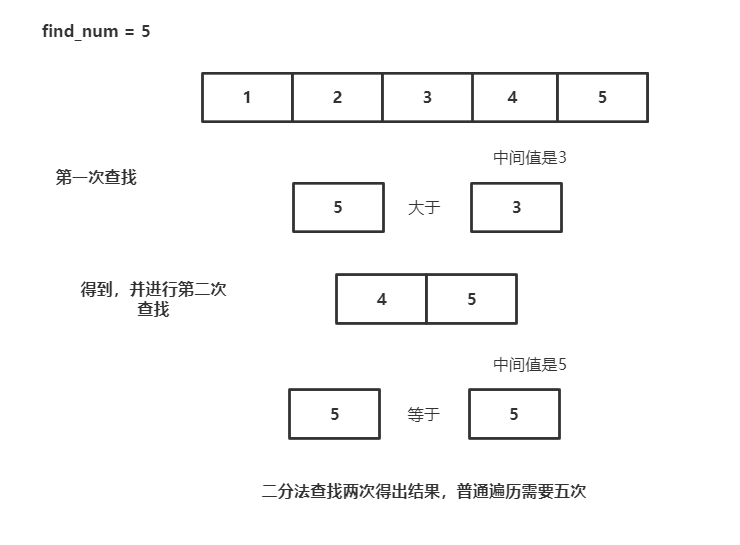
二分法图解