线段树优化建图

线段树优化建图

顾名思义，就是利用线段树建图，达到一些特殊的目的
常见的应用就是，对于一个点向一个区间连边，或者一个区间内的所有点向某一个点连边，直接连会TLE，那么就可以用到线段树优化建图

基本思想

先建一棵线段树。假如现在我们要从8号点向区间\([3,7]\)的所有点连一条权值为w的有向边

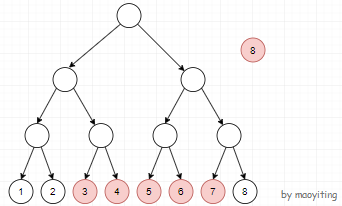
把区间\([3,7]\)拆成若干个线段树上的区间，分别与8号点单向边，如下图所示。其中黑色普通边的边权为0，粉色边的边权为w

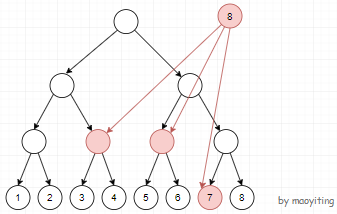
这样，原本需要连\(n\)条边的操作现在只用连\(\log{(n)}\)条边，时间复杂度也就优化到了一个\(log\)
而对于区间向点连边的操作，与上面的操作类似，但所有边的方向都需要倒过来

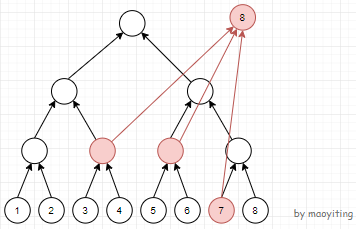
那么如果两个操作同时出现怎么处理呢？
考虑同时建出两棵线段树，一棵正着建，另一棵反着建，初始把所有的叶子节点互相连一条无向边，边权为0，代表这些叶子节点实际上反映同一些点，也就是原本的若干个单独的点。剩下的操作都和上面一样

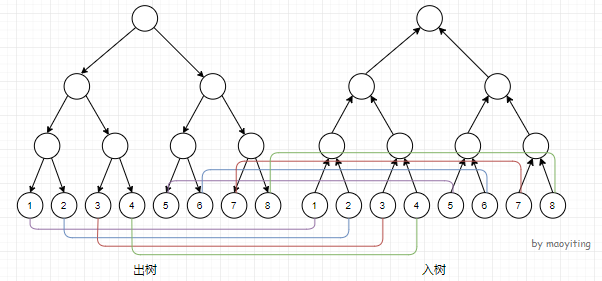
具体实现可以看一道例题

CF768B Legacy

线段树优化建图板子题。实际实现过程中，建树时利用a数组存储所有正向线段树的叶子节点的位置，由于初始化时把所有正反两向线段树的对应节点通过无向边连通了，所以这两棵线段树的叶子节点等效。对于操作一，直接把a数组记录的u，v的对应位置连边即可。对于操作二、三，把对应线段树上的区间对应的点向a数组对应位置连边，逻辑和modify相同。搜最短路时从反向树的叶子节点开始搜，因为所有线段树上连边都是单向边。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define ls(p) p<<1
#define rs(p) p<<1|1
#define N 500000
#define inf 0x3f3f3f3f3f3f3f3f

/*
思路：线段树优化建图
发现题目中有点向区间连边和区间向点连边的神秘操作，考虑什么数据结构可以
得到这样的区间，于是想到线段树。对于点向区间连边的操作，由该点向线段树
上对应区间连边。为了保证连通性，线段树上父亲节点向儿子节点连边权为0的
单向边，可以保证不产生额外贡献。对于区间向点连边同理，把父亲连向儿子的
边改为儿子连向父亲的边即可。为了避免在线段树上跑出0环(父子之间各有一条
边权为0的边)，需要正反两种操作建两棵线段树。而考虑到两棵线段树的叶子
节点与原节点一一对应，实质上是同样的节点，所以对两棵线段树上的叶子节点
之间一一连边权为0的双向边。线段树上连边时，和modify逻辑相同，只不过把
修改操作改为连边操作即可。最后跑一边最短路。 
*/

int n,m,s;
int op,u,v,l,r,w;

/*初始化图*/
struct segTree{
	int l,r;
}t[N*4+100];
struct edge{
	int to,nxt,w;
}e[N*4+100];
int a[N*4+100];
//记录所有线段树的叶子节点的位置，用于最后查询时快速获取 
int head[N*4+100],tot;
int dis[N*4+100];
bool vis[N*4+100];

void add(int u,int v,int w){
	e[++tot].to=v;
	e[tot].w=w;
	e[tot].nxt=head[u];
	head[u]=tot;
}

/*线段树模块*/
void build(int p,int l,int r){
	t[p].l=l,t[p].r=r;
	if(l==r){
		a[l]=p;
		return;
	}
	int mid=(l+r)>>1;
	//线段树父亲节点向子节点连便权为0的边 
	add(p,ls(p),0);
	add(p,rs(p),0);
	//第二棵线段树上子节点向父亲节点连边权为0的反边
	//这里提前空余出第一颗线段树的大小
	add((ls(p))+N,p+N,0);
	add((rs(p))+N,p+N,0);
	build(ls(p),l,mid);
	build(rs(p),mid+1,r);
	return; 
}

//线段树上连边
void connect(int p,int L,int R,int x,int w,int op){
	int l=t[p].l,r=t[p].r;
	if(L<=l&&r<=R){
		if(op) add(p+N,x,w);//三号操作，在反向线段树上寻找区间连边 
		else add(x,p,w);//二号操作，在正向线段树上寻找区间连边 
		return;
	}
	int mid=(l+r)>>1;
	if(L<=mid) connect(ls(p),L,R,x,w,op);
	if(R>mid) connect(rs(p),L,R,x,w,op);
	return;
}

/*最短路模块*/ 
struct dot{
	int u,d;
	bool operator <(const dot &a) const{
		return a.d<d;
	}
};

void dij(){
	priority_queue<dot> q;
	memset(dis,0x3f,sizeof(dis));
	memset(vis,0,sizeof(vis));
	dis[s]=0;
	q.push({s,0});
	while(!q.empty()){
		dot pre=q.top();//取出当前距离上一个点最近的点 
		q.pop();
		if(vis[pre.u]) continue;
		else vis[pre.u]=1;//判断是否走重复路 
		for(int i=head[pre.u];i;i=e[i].nxt){//遍历当前点的所有路径 
			int x=e[i].to;
			if(vis[x]) continue;//不走重复路(贪心策略) 
			if(dis[x]>dis[pre.u]+e[i].w){
				dis[x]=dis[pre.u]+e[i].w;//更新最短路径
				dot nxt;
				nxt.u=x;
				nxt.d=dis[x];
				q.push(nxt);//存入下一个点 
			}
		}
	}
}

signed main(){
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m>>s;
	build(1,1,n);
	for(int i=1;i<=m;i++){
		cin>>op;
		if(op==1){
			//一号操作直接连边
			cin>>u>>v>>w;
			add(a[u],a[v],w);//直接把对应线段树上的叶子节点连边 
		}else{
			//二三操作通过线段树区间连边
			cin>>u>>l>>r>>w;
			connect(1,l,r,a[u],w,op%2); 
		} 
	}
	for(int i=1;i<=n;i++){
		add(a[i],a[i]+N,0);
		add(a[i]+N,a[i],0);
		//两颗线段树对应位置的叶子节点实际上表示同一个点，连双向边 
	}
	s=a[s]+N;
	/*初始从第二棵线段树的起点对应位置开始跑最短路，因为建的单向边
	保证了只有从第二棵线段树开始往回跑才能走通*/ 
	dij();
	for(int i=1;i<=n;i++){
		if(dis[a[i]]>=inf) cout<<-1<<" ";//无解输出-1
		else cout<<dis[a[i]]<<" ";//输出答案 
	}
	return 0;
}